从明日方舟入手数据统计--盒须图

（封面源自必应，侵删）(多图预警）
由于此文的目的是数据统计学习而非游戏攻略且时间仓促，文中所用数据皆出自题主自己的明日方舟干员库，可能与实际数据有所出入。如需要权威数据请去明日方舟官方wiki

引子

上周五上司给笔者一本Tableau工具书让笔者学习。学习过程中由于手边没有成型的数据库，笔者现建了一个并打开《明日方舟》将自己现有的干员信息录了进去。
下图为本文所用数据：

SELECT 代号,身高
FROM 明日方舟干员
WHERE 明日方舟干员.性别="男" ORDER BY 身高;

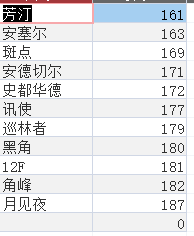
文中所用的男干员身高信息

SELECT 代号, 身高 FROM 明日方舟干员 WHERE 性别 = "女" ORDER BY 身高;

女干员身高信息（一）

女干员身高信息（二）

在笔者学习（摆弄）Tableau的过程中用每位干员的身高和性别做了一幅盒须图如下。图中以性别为划分，每个原点代表一位干员。

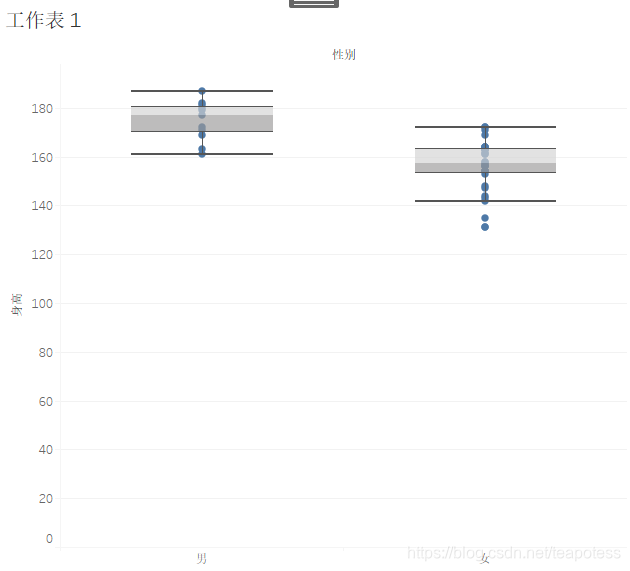
不幸的是，笔者由于长时间未复习，对于数据统计已颇为生疏而不是很明白此图的含义。查阅资料后写了如下一篇学习笔记以供后人使用。

盒须图

盒须图，英文 box and whisker graph，是用来比较数据，展示数据分布情况的统计图。因为图像似箱子，也叫箱型图。
盒须图中比较重要的几个概念：上须、上枢纽、中位数、下枢纽、下须、异常值和IQR。
将光标放在图上时可以直接得到除IQR和异常值以外的其它数据如下图：

男性干员身高箱型图数据

女性干员身高箱型图数据

中位数

中位数的概念想必很熟悉了。用白话说就是一组数据中最中间的那个数。
比如在十一位男性干员中，讯使的身高为177，在所有男干员中排第六位；那么男性干员身高的中位数就是77

身高排在第六位的讯使

由于女干员人数为三十六是个偶数，女干员身高的平均值为中间两人（此处为华法林和翎羽，身高分别是157和158）身高的平均数，为157.5
上枢纽和下枢纽
上枢纽也叫上四分位数，记作Q3。表示只有1/4的数据超过这个值。
由男性干员身高箱型图得知男性干员身高的上枢纽为180.5。总共有男性干员十一人，用mysql query验证一下：

SELECT * FROM 明日方舟干员 WHERE 性别 = "男" AND 身高 > 180.5 ORDER BY 身高;

得到如下结果：

身高超过180.5的干员共有三名，11/4=2.75

与上枢纽概念相对应，下枢纽为下四分位数，记作Q1，表示只有1/4的数据低于这个值。
举个例子，女干员身高下枢纽为153.5，用mysql query验证一下：

SELECT 代号, 身高 FROM 明日方舟干员 WHERE 性别 = "女" AND 身高 <=153.5 ORDER BY 身高;

得到如下结果：

九位干员，与开头女干员的query结果对比的话会发现与头九位干员一致

IQR

IQR 根据公式意思，为Q3与Q1的差值
比如男干员身高的IQR=Q3-Q1=180.5-170=10.5
女干员身高的IQR=Q3-Q1=163-153.5=9.5

上下须和异常值

笔者找资料的时候发现，有资料认为，上须为数据中的最大值，下须为数据中的最小值。
但是这样无法解释为什么女性干员身高的下须为阿米娅的身高（142）而非杜林或者桃金娘的身高（131）。
后来发现，此处的上下须应该表示在正常数据中的最大最小值
此处引入内外限与异常值的概念。

内外限与异常值

内限公式（为了方便，暂且就叫内上线和内下线好了）：
$$\begin{gathered} 内上限=Q_3+1.5IQR \\ 内下限=Q_1-1.5IQR \end{gathered}$$
将公式带入我们的数据：
男干员身高内上限=180.5+1.510.5=196.25
男干员身高内下限=170-1.510.5=154.25
可以看出十一位男性干员身高都在正常范围（验证过程略）。上下须即为数据的最大最小值。
将内限公式代入女性干员身高数据：
女性干员身高内上限=163+1.59.5=177.25
女性干员身高内下限=153.5-1.59.5=139.25
似乎女性干员中没有一人身高超过内上限。用query查看一下身高低于内下限的女性干员：

我们叫这三个数据异常值。大于这三个数据的都是正常值；在正常数据中阿米娅的身高（142）最低，所以下须等于阿米娅的身高。
写到这里本来该结束了，但是我们还想知道这三个异常值是否属于温和的异常值。
与温和的异常值相对的是极端的异常值，判断时涉及到外限的概念：
$$\begin{gathered} 外上限=Q_3+3\times IQR \\ 外下限=Q_1-3\times IQR \end{gathered}$$
将外下限公式带入女干员身高数据：
女干员身高外下限=153.5-3*9.5=125
一般认为在内外限之间的属于温和的异常值，在外限以外的属于极端的异常值。在对数据要求不严格的情况下温和的异常值可以当作正常值处理。
因为我们没有女性干员身高低于125，所以上面三个异常值皆可以当温和异常值处理。
Finish!

参考资料

箱形图_百度百科
盒须图的使用
明日方舟 - Arknights
特征工程之异常值处理 - 云+社区 - 腾讯云