Matlab正态分布、历史模拟法、加权移动平均线 EWMA估计风险价值VaR和回测标准普尔指数 S&P500时间序列...

拓端研究室TRL

于 2021-11-29 17:18:00 发布

阅读量198

点赞数

文章标签： matlab 开发语言

本文链接：https://blog.csdn.net/tecdat/article/details/129388349

版权

本文演示如何使用Matlab估计风险价值(VaR)的三种方法：正态分布法、历史模拟和指数加权移动平均线(EWMA)，并进行回测分析。通过对标准普尔指数(S&P500)时间序列的回测，评估VaR模型的准确性，展示不同方法在不同置信水平下的表现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

原文链接：http://tecdat.cn/?p=24480

此示例说明如何使用三种方法估计风险价值 (VaR) 并执行 VaR 回测分析。这三种方法是：

正态分布
历史模拟
指数加权移动平均线 (EWMA)

风险价值是一种量化与投资组合相关的风险水平的统计方法。VaR 衡量指定时间范围内和给定置信水平的最大损失量。

回测衡量 VaR 计算的准确性。使用 VaR 方法，计算损失预测，然后与第二天结束时的实际损失进行比较。预测损失和实际损失之间的差异程度表明 VaR 模型是低估还是高估了风险。因此，回测回顾数据并有助于评估 VaR 模型。

本示例中使用的三种估计方法在 95% 和 99% 的置信水平下估计 VaR。

加载数据并定义测试窗口

加载数据。本例中使用的数据来自标准普尔指数从 1993 年到 2003 年的时间序列收益率。

tik2rt(sp);

将估计窗口定义为 250 个交易日。测试窗口从 1996 年的第一天开始，一直持续到样本结束。

WinSze = 250;

对于 95% 和 99% 的 VaR 置信水平。

p = \[0.05 0.01\];

这些值意味着分别有至多 5% 和 1% 的概率发生的损失将大于最大阈值（即大于 VaR）。

使用正态分布方法计算 VaR

对于正态分布法，假设投资组合的损益呈正态分布。使用此假设，通过将每个置信水平的_z_分数乘以收益率的标准差来计算 VaR 。由于 VaR 回溯测试对数据进行追溯，因此“今天”的 VaR 是根据过去_N_ = 250 天（但不包括“今天”）的收益率值计算得出的。

for t = TtWnow
    i = t - TsWidoSrt + 1;
    Esationdw = t-EtiWinwSze:t-1;
    gma = std(Returns(tmWinow));
    Noa95(i) = -Zscre(1)*Sima;
    Nrml99(i) = -Zsore(2)*Sigma;
end


plot(DaeRtuns(TsWidw),\[Nrm95 oma99\])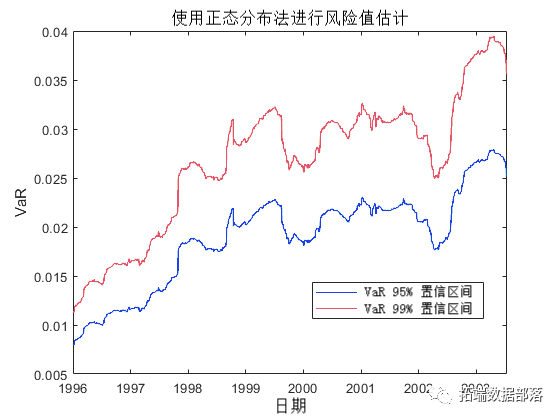

正态分布方法也称为参数 VaR，因为它的估计涉及计算收益率标准差的参数。正态分布方法的优点是简单。然而，正态分布方法的弱点是假设收益率是正态分布的。正态分布方法的另一个名称是方差-协方差方法。

使用历史模拟方法计算 VaR

与正态分布方法不同，历史模拟 (HS) 是一种非参数方法。它不假设资产收益的特定分布。历史模拟通过假设过去的损益可以作为下一个收益期的损益分配来预测风险。“今天”的 VaR 计算为“今天” 之前最后_N 次_收益率的 _第 p_个分位数。

for t = Tstidow
    i = t - Tsidwtt + 1;
    Htrl95(i) = -qate(X,pVR(1));
    Hii99(i) = -qatie(X,pVaR(2));


fiure;
plot(Dtr(Ttow),\[Hic95 Hstrl99\])