R语言GARCH族模型：正态分布、t、GED分布EGARCH、TGARCH的VaR分析股票指数

于 2022-12-23 16:44:32 发布
阅读量1.8k 收藏 31
点赞数
CC 4.0 BY-SA版权
文章标签： r语言 开发语言
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/tecdat/article/details/129390501
本文利用R语言探讨GARCH族模型，包括GARCH(1,1)、EGARCH、GJR-GARCH和APARCH，分析股票型券商理财指数收益率，进行正态性、自相关性、异方差性和平稳性检验，以计算VaR。数据表明序列非正态分布，存在自相关和ARCH效应，适合用条件异方差模型建模。" 16339553,1113818,C# 中的数值转换：从字符串到字节数组,"['C#编程', '数据类型转换', '串口通信', '数值处理', 'BitConverter']

全文链接：http://tecdat.cn/?p=31023

如何构建合适的模型以恰当的方法对风险进行测量是当前金融研究领域的一个热门话题（点击文末“阅读原文”获取完整代码数据）。

VaR方法作为当前业内比较流行的测量金融风险的方法,具有简洁,明了的特点,而且相对于方差来讲,更多的将投资人的损失作为风险具有更好的合理性。

我们和一位客户讨论如何在R软件中处理GARCH族模型。

数据的选取

本文选取Wind资讯发布的股票型券商理财指数作为数据处理对象。选取的时间期间为2011年1月4日至2015年11月24日，共1187个交易日。该指数基日为2007年12月31日，基点为1000点。

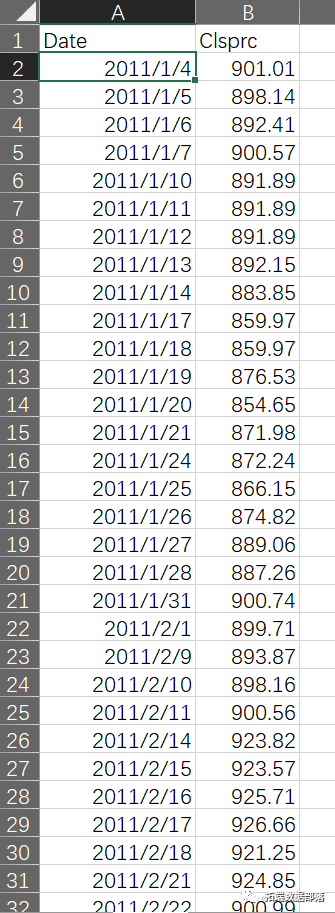
13d8d0035e0e5e51153313a1b87e0f27.png

收益率的计算

采用对数收益率对指数收盘点位进行计算，表达式为

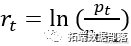
56958b28999eefabcae4df8e110f5324.png

记为序列 。由图观察可知，该收益率序列存在波动聚集现象。

clpr<-stock$Clsprc
yield<-diff(log(clpr))
ts.plot(yield)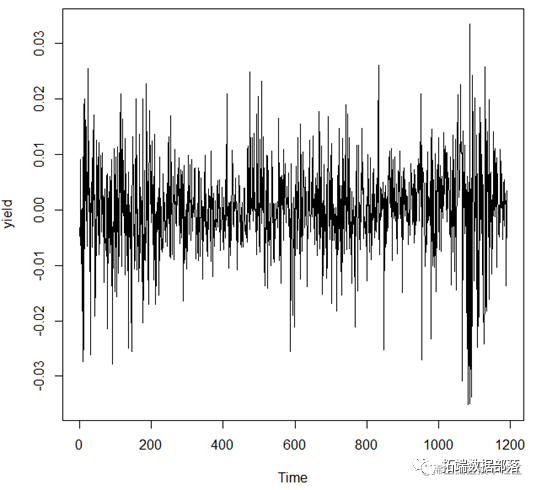

2392132b87fea2929740d78dd079b854.png

基本特征分析

对序列 进行基本统计分析，结果如表所示：

summary(yield)
sd(yield)
var(yield)

表 指数日收益率基本统计表****

Min. 1st Qu. Median Mean 3rd Qu. Max. Sd skewness' kurtosis
-0.03517 -0.00389 0.0003749 0.0001963 0.00473 0.03348 0.008163353 -0.4018462 2.169439

由表可知，收益率序列 的最小值为-0.03517，最大值为0.03348，平均值为0.0001963，标准差为0.008163353。偏度为-0.4018462，表现为右偏。峰度为2.169439，该分布比正态分布更陡峭。

1、正态性检验

对指数的日收益率序列进行正态性检验。检验方法采用Jarque-Bera统计量。检验结果显示Jarque-Bera统计量为261.3839，P值接近0，拒绝对数收益率服从正态分布的原假设，表明序列为非正态分布。

表 Jarque-Bera检验结果

检验方法 统计量 P值
Jarque-Bera 261.3839 < 2.2e-16

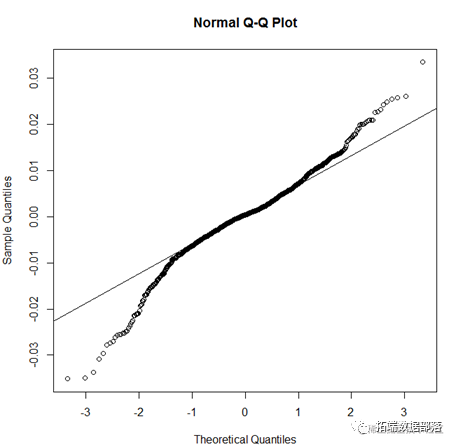
为了进一步探究序列 的分布形态，对样本数据作直方图、QQ图。由图可见，该收益率序列的尾部更长更厚，且其分布存在明显的不对称的现象，为非正态分布。

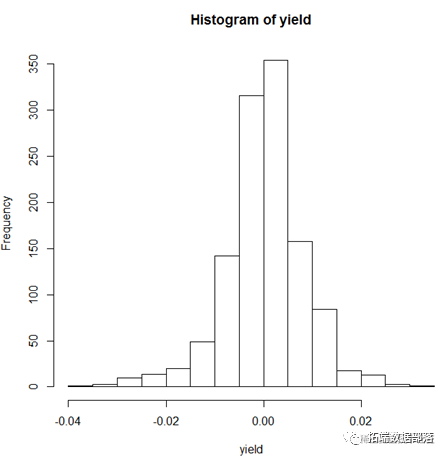
e69023d148830e159910df353475b57b.png

03befaf41219f9f889cde86c8a23efe0.png

2、自相关性检验

对指数的日收益率序列的自相关性进行检验。检验方法采用Ljung-Box检验。表中LB2(12)指滞后期为12的收益率平方的Ljung-Box统计量，该统计量在无序列相关的零假设下，服从自由度为12的 分布。具体检验结果如下：收益率平方的Ljung-Box统计量为34.1853，P值为0.0006306，拒绝无自相关的零假设，表明收益率的平方存在自相关现象。

表 Ljung-Box检验结果

检验方法 统计量 P值
LB2(12) 34.1853 0.0006306

为了进一步探究序列的自相关性，对序列作ACF、PACF图。由图可见，该收益率序列存在自相关现象。

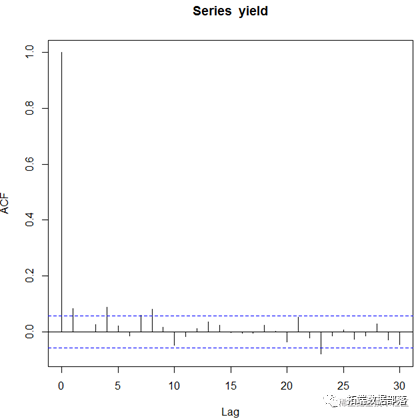
b8fb1e7424aea663829ef7b1b6773a36.png

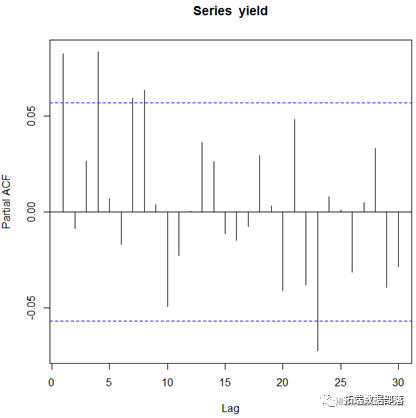
b3de31938b47bd0e4673283eafe8caa4.png

3、异方差性检验

对指数的日收益率序列进行异方差性检验。检验方法采用ARCH-LM检验。表中LM(12)指ARCH效应的拉格朗日乘数检验，在没有ARCH效应的零假设下，统计量服从自由度为12的 分布。具体检验结果如下：LM统计量为170.9818，P值接近0，故拒绝无ARCH效应的零假设，表明收益率序列存在ARCH效应。

表 ARCH-LM检验结果

检验方法 统计量 P值
LM(12) 170.9818 < 2.2e-16

4、平稳性检验

在时间序列模型中，序列的平稳性会直接影响到模型的拟合效果，非平稳的序列容易产生谬误回归（Spurious Regression）。本节将采用 ADF 检验来对收益率序列进行单位根检验。检验结果显示Dickey –Fuller值为-9.7732（滞后10阶），P值小于0.01，故拒绝存在单位根的原假设，认为该收益率序列是平稳的。

表 ADF检验结果

检验方法 统计量 P值
ADF -9.7732 <0.01

综上，收益率序列存在明显的尖峰厚尾效应，JB检验同样否认了收益率服从正态分布的假设。LM检验表明收益率存在ARCH效应，而LB检验表明收益率的平方存在自相关现象，因此可以采用条件异方差模型来分析收益率序列的波动特性

GARCH族模型的建立

本文将分别采用基于正态分布、

最低0.47元/天 解锁文章
博客
视频讲解|Python遗传算法GA在车辆路径规划VRP数据优化中的应用
10-16 268
突变操作是随机修改路径中的某个城市编号，比如把路径“0 1 2 3 0”中的“2”改成“5”，变成“0 1 5 3 0”。但这一步很容易出现“重复访问”的问题——比如原路径里已经有“5”，修改后就会重复。所以突变后必须做“合法性修复”：比如刚才的例子，把“2”改成“5”后，路径里出现了两个“5”，这时就要把原来的“5”改成“2”，确保每个城市只出现一次。这一痛点的本质，正是车辆路径规划（VRP）问题——它是旅行商问题（TSP）的延伸，却因“多车辆、多约束”的特性，在实际业务中更难通过传统算法高效求解。
博客
专题：2025年AIAgent智能体行业价值及应用分析报告：核心趋势、经济影响与治理框架|附700+份报告PDF、数据仪表盘
10-16 374
大企业要建“AI中心”，整合数据、统一模型，避免各部门重复花钱，比如沃尔玛的AI供应链中心，统一管理全球的库存数据。World Economic Forum的报告显示，现在仅1%的组织能“全面实施负责任AI”，20%是“部分实施”，50%还在“计划中”，29%“没实施”。还有一个趋势是“AI项目越来越多”：2023年才1000个，2024年1500个，2025年预计2000个，2026年2500个——企业不再是“试点”，而是“规模化落地”，比如沃尔玛用AI管理全球的供应链，不是只在某几家店试手。
博客
专题：2025企业出海数字化白皮书：多领域机遇与风险管理|附200+份报告PDF、数据仪表盘汇总下载
10-14 93
中药则需突破“文化认知”与“标准合规”壁垒，在东南亚、非洲等市场寻找突破口。：本月内完成墨西哥（墨西哥城）、泰国（曼谷）的本地供应商筛选（至少各3家），针对北美市场备货EPA认证的发动机配件，东南亚市场备货单价低于100美元的维修件（如滤清器、刹车片），将交货周期从45天缩短至30天以内。从汽配产业的全球供应链布局，到创新药的技术出海突破，再到中药的文化价值输出，不同行业的出海路径虽各具差异，但均需在“风险防控”与“价值落地”之间找到平衡——这既是企业全球化的核心命题，也是本次报告洞察的核心主线。
博客
专题：2025汽车行业数字化转型研究报告|附270+份报告PDF、数据仪表盘汇总下载
10-14 66
据懂车帝巨懂车&巨量云图《汽车行业心智趋势报告》，2025年抖音平台上，油混车型心智增长率达1869%，增程车型达1457%，保养相关话题增长率达780%——这一趋势表明，消费者对“续航焦虑”的担忧仍未完全缓解，油混、增程等“无续航焦虑”的技术路线更受青睐，同时“购车后保养成本”成为决策关键因素。铝合金的核心优势在于：密度仅为钢材的1/3，可实现新能源汽车减重20%-30%，且加工工艺成熟、成本低于镁合金与碳纤维，适合大规模应用，当前已广泛用于电池壳、车身结构件、轮毂等核心部件。
博客
DeepSeek、LangGraph和Python融合LSTM、RF、XGBoost、LR多模型预测NFLX股票涨跌|附完整代码
10-14 289
所有代码、数据都经过实际业务校验，新手跟着做也能落地！最新的DeepSeek-r1/DeepSeek-V3用了多专家机制（MoE），总参数量6710亿，但每次计算只启用370亿参数，既保证推理准度（算技术指标、分析趋势不翻车），又不耗资源（普通电脑也能跑），特别适合股票量化分析这种“要精度也要速度”的场景。数据核心字段很清晰：日期（Date）、开盘价（Open）、最高价（High）、最低价（Low）、收盘价（Close）、调整后收盘价（Adj Close）、成交量（Volume），覆盖股价分析的全维度。
博客
专题：2025中国人工智能医疗健康研究报告（智慧医院+医保+器械+AI）深度洞察|附130+份报告PDF、8个数据仪表盘汇总下载
10-10 82
智慧医院产业链涵盖“技术提供方（网络设备商、软件服务商）-医院应用层（门诊、病区、手术室）-患者受益端”三环节，过去受制于“网络不稳定、部署成本高、业务中断率高”三大痛点——南京鼓楼医院（应用端）曾因挂号系统响应滞后导致患者平均候诊超1小时，武汉协和医院（落地端）传统网络部署1个病区需10天，南方医科大学深圳医院（场景端）移动查房时PDA因漫游丢包每天浪费护士30分钟，倒逼技术层（如华为SDN、零漫游方案）与应用层深度融合。移动查房业务中断率15%（场景痛点），严重影响医嘱录入（医护端）。
博客
OpenCV+MediaPipe+Python集成学习中风后肢体运动功能康复视频三维数据与FMA量表智能评估系统|附代码数据
10-10 374
全文链接：tecdat.cn/?p=44034原文出处：拓端数据部落公众号分析师：Xuanlu Dai在中风康复领域，肢体运动功能评估是制定康复方案、判断康复效果的核心环节。传统评估依赖康复师人工观察，基于Fugl-Meyer（FMA）量表给出主观评分，存在效率低、误差大、难以量化运动细节等问题（点击文末“阅读原文”获取完整智能体、代码、数据、文档）。随着计算机视觉与数据分析技术的发展，通过视频提取肢体运动数据并自动化评估成为解决这一痛点的关键方向。一、引言本文方案改编自分析师团队过往完成的中风康复机构咨询
博客
视频讲解|贝叶斯优化的循环注意力RNN、神经微分方程对百威啤酒产线时空动态数据预测
09-30 908
咱们这套模型，把“时序分解的可解释性”和“神经微分、注意力的高精度”结合起来，还通过动态残差、重构学习、联合损失这些方法，解决了产线数据“阶数误差”和“复杂依赖”的问题。循环神经网络（RNN）在时序预测里挺常用，但产线数据的非线性、时空耦合特性太强，普通RNN想同时抓长短期规律，就“力不从心”了——要么学不进去，要么预测结果偏差大。产线数据太复杂，直接预测费劲。自注意力门控：不同时间的输入和上一时刻状态，通过自注意力学一学，学到的结果当“门控权重”，这样不同数据就能被“区别对待”，复杂依赖也能抓得更准～
博客
专题：2025医药行业数智赋能与AI应用全景研究报告|附200+份报告PDF、数据仪表盘汇总下载
09-30 123
如今，生产运营平台能实时上传车间数据，AI工具可提前预警库存风险，数智化已从“可选项”变为“生存项”。我们梳理了制药、器械、流通、零售四大领域的数智化实践，结合AI在研发、人力、供应链的应用案例，提炼出“场景落地-人才匹配-风险规避”的三维解决方案，无论是药企决策者规划转型路径，还是供应链负责人优化溯源体系，都能在此找到可复用的工具与方法。：别追求“一步到位”，从“小场景”切入，先上线库存预警机制，实时监控近效期药品与不动销产品，验证效果后再扩展到生产、营销领域，社群内有《小场景数智化落地清单》可领。
博客
2025年AI大模型赋能智能座舱研究报告：技术、资本与市场|附20+份报告PDF、数据仪表盘汇总下载
09-29 77
语音助手、VR/元宇宙等赛道融资事件数年均增长15%，其中HUD抬头显示的融资占比从2022年的2%升至2024年的6%，核心驱动力是“AR技术与HUD的融合”——当前主流AR-HUD已能将导航路标、障碍物预警等虚拟信息叠加在真实道路上，解决“驾驶分心”的核心痛点，而这一功能的落地，依赖域控制器的算力支撑与AI算法的场景识别能力，形成“硬件+软件”的投资联动效应。30万以上用户在意“交互沉浸感”，重点展示AR-HUD的“虚拟路标叠加”“多屏内容流转”，让用户直观感受“视线不离开路面的便捷”。
博客
专题：2025零售数字化与即时零售竞争洞察报告|附130+份报告PDF、数据仪表盘汇总下载
09-29 104
具体应对方案：1. 进群获取《补贴成本测算表》，输入“客单价、补贴金额、配送成本”，自动算出“补贴后单均利润”，避免“为单量盲目参与活动”；校园便利店经营者：结合校园社团的“场景化需求”，下周联系2-3个高校社团（学生会、动漫社、电竞社），定制“社团专属套餐”——比如给动漫社做“二次元包装零食套餐”（印动漫角色的薯片+饮料），给电竞社做“熬夜补给包”（能量饮料+坚果），用“社团折扣卡”（持社团证享9折）吸引学生复购，同时收集用户口味反馈（如是否需要低糖零食），优化下周进货清单；
博客
专题：2025年AIAgent智能体行业洞察报告|附110+份报告PDF、数据仪表盘汇总下载
09-29 64
参考某城商行“先试后买”的策略，先申请试用版，看能不能对接自家系统，再决定付费。：AI Agent靠数据说话，先梳理内部数据，比如HR的岗位需求模板、财务的指标定义（如“营收”是含税还是不含税），参考沙丘智库说的“语义层构建”，统一数据口径和业务语义——不然数据混乱，AI Agent出的结果也不准，反而添乱。AI Agent能在2025年落地，关键是它不搞“技术炫技”，而是盯着每个行业的“核心痛点”——HR怕招聘效率低，零售怕报告耗时长，制造怕研发慢，这些痛点用AI Agent都能解决，且效果有数据支撑。
博客
专题：2025中国出口跨境电商发展趋势研究报告：市场增长、支付金融、出海营销|附370+份报告PDF、数据仪表盘汇总下载
09-29 284
全球经济增速放缓，消费者把钱都花在了“刀刃上”——33%的人会转买更便宜的品牌，34%直接少买非必需品，这种“抠”不是小气，是对“高性价比”的精准追求。看全球，跨境电商年均复合增长率17%，中国市场15%的增速虽稍低，但底子扎实——亚马逊上35%的中国卖家销量，都来自一年内的新选品，这就是“靠创新不靠低价”的底气。全球跨境支付市场年均复合增长8.4%，看着不算快，但细分领域很猛——收款服务增速10.7%，供应链金融更冲到11.9%，这说明大家不满足于“能收到钱”，更要“收得划算、用得高效”。
博客
JupyterLab+PyTorch：LoRA+4-bit量化+SFT微调Llama 4医疗推理数据集应用|附代码数据
09-29 974
在大语言模型（LLM）落地医疗推理场景的过程中，Meta推出的Llama 4系列（含Scout与Maverick两个开源权重模型）因性能优异备受关注，但该系列模型微调门槛极高——Llama 4 Scout需4张H100 GPU，Maverick需8张，高额硬件成本让多数企业与学生望而却步。本文内容改编自项目的技术沉淀，将从“云平台配置→模型加载→数据处理→微调训练→效果验证→模型部署”全流程，拆解低成本微调Llama 4 Scout的实操方案，尤其聚焦医疗推理场景下的prompt设计与模型优化细节。
博客
TCN时序卷积网络、CNN、RNN、LSTM、GRU神经网络工业设备运行监测、航空客运量时间数据集预测可视化|附代码数据
09-22 809
本专题围绕 “TCN 模型在时序数据处理中的应用” 展开，包含两篇核心内容：第一篇以 FordA 工业设备时序数据集为对象，基于 Python 和 TensorFlow/Keras，对比 CNN 与 TCN 的差异，详解 TCN 的膨胀卷积、因果填充与残差块原理，通过构建 “滤波器数量 + 输出层结构” 不同的三个 TCN 模型，验证最优分类方案；时序预测的核心前提是“高质量输入数据”，本部分通过加载数据、探索性分析、季节性检测、数据分割与归一化，以及协变量构建，为后续模型训练提供标准化输入。
博客
Python实现Elman RNN与混合RNN神经网络对航空客运量、啤酒产量、电力产量时间序列数据预测可视化对比
09-19 982
研究中，我们基于Python与NumPy手动实现Elman RNN、Jordan RNN和Multi-RNN，针对航空客运量（Air Passengers）、啤酒产量（Beer Production）、电力产量（Electricity Production）、黄金价格（Gold Price）、雅虎股票（Yahoo Stock）五类典型时间序列数据，结合多项式去趋势与Min-Max归一化预处理，通过网格搜索调优超参数，并采用MSE、MAE、RMSE、MAPE四项指标及Friedman检验验证模型有效性。
博客
专题：2025全球能源转型与中国新能源产业机遇研究报告|附270+份报告PDF、数据仪表盘汇总下载
09-19 165
原文链接：tecdat.cn/?p=43908原文出处：拓端抖音号@拓端tecdat分析师：Xiongtao Zou2025年全球能源格局正面临“双重考验”：一面是中国光伏风电装机突破11.8亿千瓦、清洁能源投资冲至2万亿美元，成为全球绿色转型的“压舱石”；另一面是全球南方国家深陷1.3万亿美元的年度投资缺口，AI数据中心400TWh的能耗又给电网安全添了新负担（点击文末“阅读原文”获取专题报告合集PDF版本）。更关键的是，能源转型早已不只是“减碳议题”——从美欧对中国新能源产品加征关税，到中国持续落地《可
博客
专题：2025预制菜行业洞察报告：消费者行为、竞争格局|附40+份报告PDF、数据仪表盘汇总下载
09-17 132
即烹食品”以48.8%的选择率最高，这类产品的供应链核心是“半成品预处理”——比如即烹牛肉，中央厨房完成切配、腌制，消费者只需简单煎炒，既保留烹饪感，又省去原料处理步骤，对B端来说，能降低门店人工成本；水产预制菜企业重点布局酸菜鱼品类时，可开发200-300g小份装，适配露营场景（52.8%消费者接受度），供应链端联合区域冷链企业（如华鼎冷链）做“分布式仓储”，将配送成本降低15%-20%——参考盒马“露营罐罐火锅”的包装设计，搭配便携加热包，既能覆盖户外渠道，又能减少冷链损耗。
博客
专题：Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据
09-17 843
本文将从零构建贝叶斯线性回归的完整流程：先回顾Frequentist线性回归的核心理论，再引入贝叶斯更新原理，接着详解MCMC Metropolis-Hastings采样的实现逻辑，最后通过Python生成合成数据集（实际业务中的线性关系数据），完成建模与结果验证，并与Frequentist方法对比参数准确性。：基于合成数据集的验证表明，贝叶斯模型的参数后验分布能准确逼近真实值，且Frequentist估计值落在高概率区域内，说明模型在“线性关系拟合”场景中可靠性高，可迁移至实际业务数据。
博客
专题：2025中国消费市场趋势与数字化转型研究报告|附360+份报告PDF、数据仪表盘汇总下载
09-15 340
毕马威说东南亚和北美是主要目的地——东南亚靠华人多、文化近，北美靠消费力强，但要改：泡泡玛特在新加坡搞“配货制”，在日本却做小巧的IP手办，因为日本人更爱“精致小物件”，这就是本地化。这不是中国人不愿花，而是过去更习惯“存钱”，但2025年上半年人均可支配收入实际增长5.4%，加上“以旧换新”政策拉动力电消费，未来这部分“蓄水”早晚会释放。现在说AI，早不是“高大上的概念”了——94%的用户会用AI规划健身、找学习内容，87%会让AI给社交建议，甚至36%的人把AI当“好朋友”，压力大时会倾诉。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值