本文介绍了定积分的概念及其与物理学中位移的联系，通过推导证明了牛顿-莱布尼茨公式，即∫abf(t)dt=F(b)−F(a)，揭示了微积分的基础及其在各理工科学科中的广泛应用。学习微积分的重要性往往在多年后才能显现。
本文始发于个人公众号：TechFlow，原创不易，求个关注
今天是高等数学专题的第13篇文章，我们来看看定积分究竟应该怎么计算。
定积分的实际意义
通过之前的文章，我们基本上熟悉了定积分这个概念和它的一些简单性质，今天终于到了正题，我们要试着来算一算这个积分了。
我们先来回忆一下对定积分的直观感受，它可以代表一段曲形面积，比如：
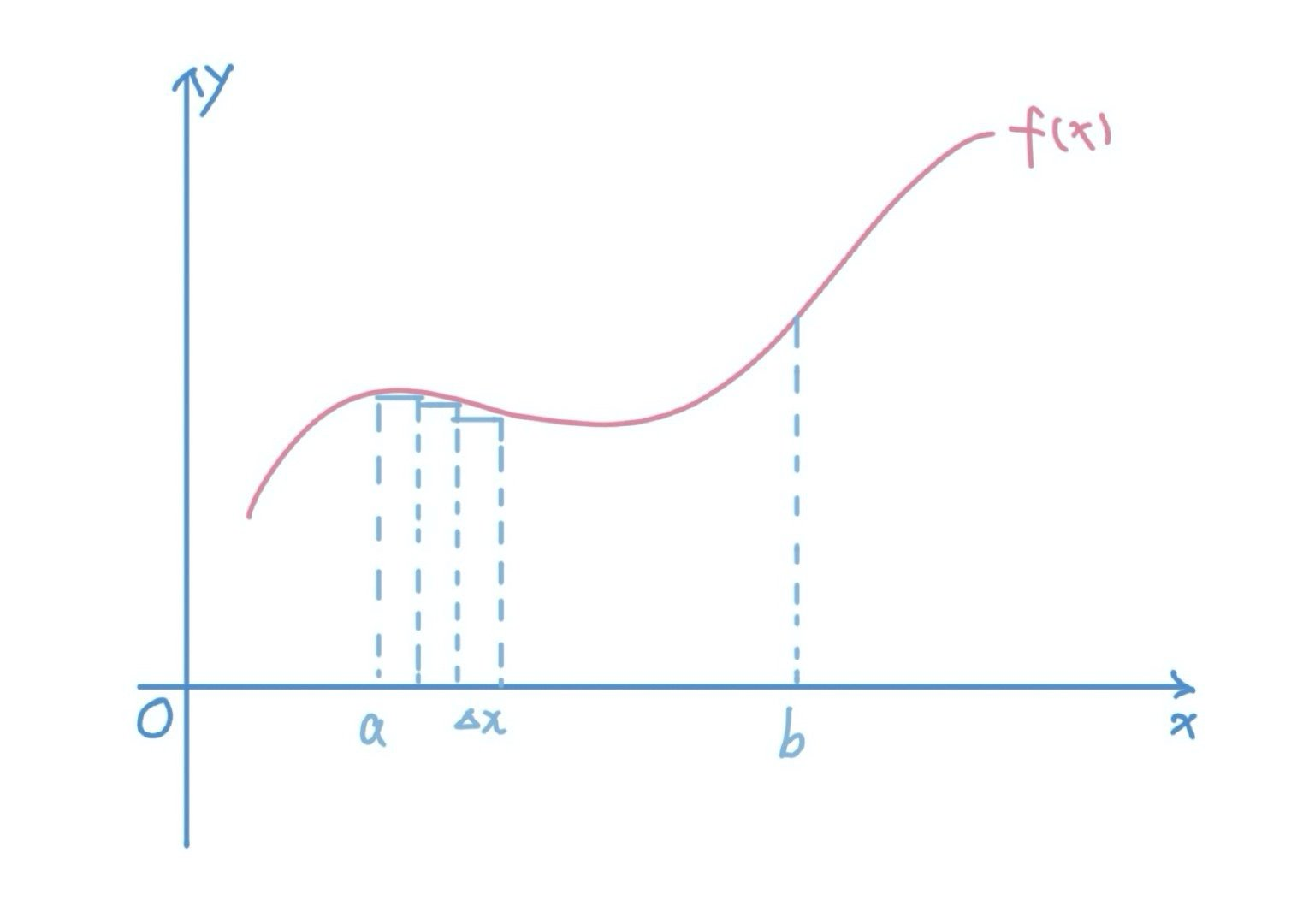
如果我们把上图当中的f(x)看成是速度函数，x轴看成是时间，那么f(x)就表示时刻x时物体运动的速度。那么我们把所有瞬时移动的距离累加，就得到了物体在某个时间段内的位移矢量，而这个位移长度恰好就是我们曲形的面积。我们把定积分和物理上的位移进行挂钩之后，很容易得出一个结论，在物理学上，一个物体发生的位移和时间也是一一映射的关系，所以这也是一个函数。
有了这个结论之后，我们就可以做一个假设，假设一个函数s(t)满足：
s ( t ) = ∫ a t f ( t ) d t s(t) = \int_a^t f(t)dt s(t)=∫atf(t)dt
其中的a是一个定值，我们可以认为是位移发生的起始时刻，s(t)就是物体位移和时间的函数。所以a到b这段时间内发生的位移就等于 s ( b ) − s ( a ) = ∫ a b f ( t ) d t s(b) - s(a) = \int_a^b f(t)dt s(b)−s(a)=∫abf(t)dt.
计算推导
当我们把定积分和物理位移挂钩的时候，我们距离求解它已经很接近了。
根据物理上的定义，物体的运动速度其实就等于位置矢量随时间的变化率，虽然不够严谨，但其实这是一个微分量，可以近似看成是位移函数的导数。当然这个只是直观的认识，我们还需要用严谨的数学语言来表达。
我们假设f(x)函数在区间[a, b]上连续，并且 Φ ( x ) = ∫ a x f ( t ) d t , ( a ≤ x ≤ b ) \Phi(x) = \int_a^x f(t)dt, (a \leq x \leq b) Φ(x)=∫axf(t)dt,(a≤x≤b)，我们试着证明 Φ ′ ( x ) = f ( x ) \Phi'(x) = f(x) Φ′(x)=f(x)。
我们取一个绝对值足够小的 Δ x \Delta x Δx，使得 x + Δ x ∈ ( a , b )
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
