【图解例说机器学习】逻辑回归 (Logistic Regression)

在我们日常生活中，我们经常会遇到使用到预测的事例，而预测的值一般可以是连续的，或离散的。比如，在天气预报中，预测明天的最高温，最低温(连续)，亦或是明天是否下雨(离散)。在机器学习中，预测连续性变量的模型称为回归(Regression)模型，比如标准的线性回归，多项式回归；预测离散型变量的模型称为分类(Classification)模型，比如这里要介绍的逻辑回归和以后要提到的支持向量机(SVM)等。

---

回归与分类的联系

根据上面的论述，回归与分类的区别在于预测的变量是否是连续的。具体来说，回归是求得一个函数$y_r=f(\mathrm{x})$进行输入变量 $\mathrm{x}$ 到连续型输出变量 $y_r$ 的映射；分类是是求得一个函数$y_c=f(\mathrm{x})$进行输入变量 $\mathrm{x}$ 到离散型输出变量 $y_c$ 的映射，可以将其看成是一个分段函数。

一个直觉的想法是，通过一个函数$y_c=g(y_r)$可以把回归模型转化为分类模型，即$y=g(f(\mathrm{x}))$。逻辑回归正是用到了这一思想：逻辑回归是在回归模型的基础上，将回归模型的输出$y_r$映射成离散输出$y_c$，我想这也是为什么取名逻辑回归而不是逻辑分类吧。 需要注意，逻辑回归是用来解决分类问题的。

---

一个例子

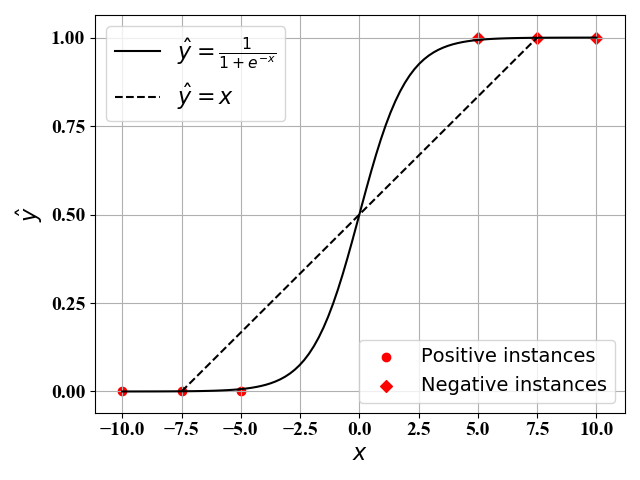
如图1所示，假定我们有6个样本点，3个正例($y=1$)和3个反例($y=0$)。我们对其进行线性回归。当使用最简单的线性回归模型(即$\hat{y}={\omega }_0+{\omega }_{1}x$)时，我们可以得到其最佳函数表达式为$\hat{y}=x$，如图中虚线所示。当我们使用复杂的回归模型时(比如考虑$x$的高阶项)时，此时我们可以得到一个十分接近$\hat{y}=\frac{1}{1+e^{-x}}$的函数表达式。显然，后者的效果更好，但是复杂度十分高。

图1

从分类问题的角度来看，我们并不关心每一个样例点的预测值，只是关心最终每个样例点属于哪一类。分类问题就是找到一个好的分段函数，使得输入$x$在不同区间的时候，输出$\hat{y}$分成不同类。比如图1中，当$x<0$时，判别为类别$0$；当$x>0$时，判别为类别$1$，于是我们有如下分段函数表达式：
$$\hat{y}=\{\begin{array}{l}0x<0\\ 1x>0\end{array}\text{\hspace{1em}(1)}$$
分段函数(1)虽然形式简单，但是在$x=0$处不可导，不利于后面使用梯度下降法。为此，一般通过图1中的Sigmoid函数$\hat{y}=\frac{1}{1+e^{-x}}$来近似。

模型描述

在逻辑回归中，输入 $\mathrm{x}$ 与输出 $\hat{y}$ 的函数表达式为
$$\hat{y}=g(h(\mathrm{x}))\text{\hspace{1em}(2)}$$
其中，$\mathrm{z}=h(\mathrm{x})={\omega }_0+{\mathrm{w}}^{\mathrm{T}}\varphi (\mathrm{x})$ 是线性回归的函数表达式，$g(\mathrm{z})=[1+e^{-\mathrm{z}}{]}^{-1}$ 是Sigmoid函数。

注意：Sigmoid函数$g(\mathrm{z})$的作用是将线性回归的输出$\mathrm{z}=h(\mathrm{x})$映射到$0$到$1$的取值范围。

---

误差函数

损失函数有很多种选择：在线性回归中，我们一般采用的是最小均方误差，即$E={\sum }_i({\hat{y}}_i-y_i{)}^2$ 。然而在逻辑回归中，使用最小均方误差后，误差函数$E$对于变量$\mathrm{w}$不一定是凸函数，不利于求解。为此，有人提出了使用交叉熵作为误差函数：
$$E=-\sum _{i=1}^N[y_i\log {\hat{y}}_i+(1-y_i)\log (1-{\hat{y}}_i)]\text{\hspace{1em}(3)}$$

---

问题求解

逻辑回归就是寻找一组参数 w ˉ = { ω 0 , w } \bar{\mathrm w}=\{\omega_0,\mathrm w\} wˉ={ω0​,w} 使得误差函数值最小，即：
$$\underset{\mathrm{w}}{\min }E=-\sum _{i=1}^N[y_i\log {\hat{y}}_i+(1-y_i)\log (1-{\hat{y}}_i)]\text{\hspace{1em}(4)}$$
这是一个凸优化问题，和线性回归类似，我们可以考虑的方法有正规方程法和梯度下降法。但是由于该函数表达式比较复杂，正规方程法一般无法得到其解析解。为此，下面我们采用梯度下降法进行求解。

梯度下降法

梯度下降法的一般表达式如下：
$${\bar{\mathrm{w}}}^{t+1}={\bar{\mathrm{w}}}^t-\eta \frac{\partial E}{\partial \bar{\mathrm{w}}}\text{\hspace{1em}(5)}$$
对于每一个训练样例${\mathrm{x}}_i$采用求导的链式法则，我们有：
$$\frac{\partial E}{\partial {\omega }_j}=\frac{\partial E}{\partial {\hat{y}}_i}\frac{\partial {\hat{y}}_i}{\partial z_i}\frac{\partial z_i}{\partial {\omega }_j}\text{\hspace{1em}(6)}$$
将公式(2)和(3)带入可得
$$\frac{\partial E}{\partial {\hat{y}}_i}=\frac{1-y_i}{1-{\hat{y}}_i}-\frac{y_i}{{\hat{y}}_i},\frac{\partial {\hat{y}}_i}{\partial z_i}={\hat{y}}_i(1-{\hat{y}}_i),\frac{\partial z_i}{{\omega }_j}=x_i^{(j)}\text{\hspace{1em}(7)}$$

$$\frac{\partial E}{\partial {\omega }_j}=({\hat{y}}_i-y_i)x_i^{(j)}$$

最终，逻辑回归问题的迭代表达式为
$${\omega }_j^{t+1}={\omega }_j^t-\eta \sum _{i=1}^N({\hat{y}}_i-y_i)x_i^{(j)}\text{\hspace{1em}(8)}$$

---

算法实现

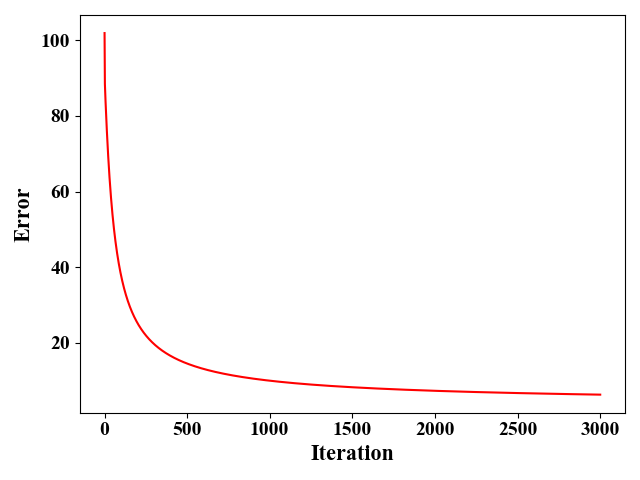
我们这里使用iris数据集(sklearn库中自带)，这里面有150个训练样例，4个feature, 总共分3类。我们只考虑了前2个feature，这么做是为了在二维图中展示分类结果。并且将类别2和类别3划分为同一类别，这样我们考虑的是一个二分类问题。图2给出了使用梯度下降法时，误差的收敛情况。这里我们假设学习率 $\eta =1e^{-3}$，算法差不多需要迭代3000次左右收敛。

图2

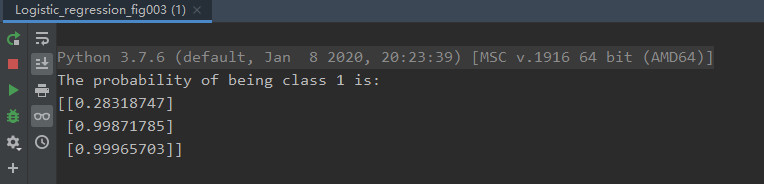
在这150个样例中，我们取出第25,75,125个样例作为测试样例(其label分别为0,1,1)，其他147个作为训练样例。下图为测试结果：

图3

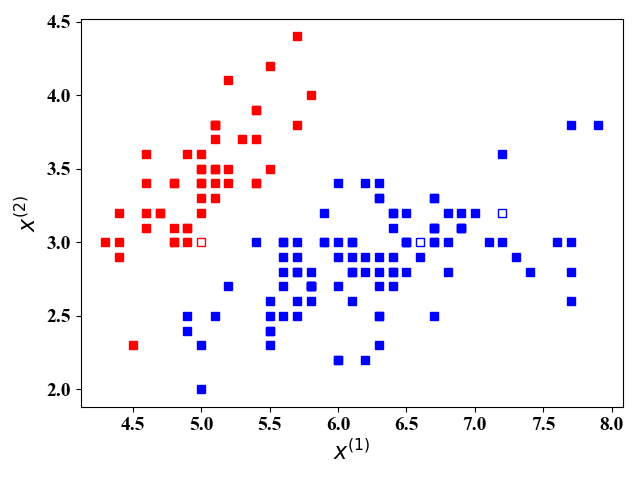
图4给出了这3三个测试样例的预测结果，其输出$\hat{y}$就是这3个测试样例属于类别 $1$ 的概率。当$\hat{y}>0.5$时，判别为$1$，否则判别为$0$。图5更加直观地显示了图4的判别结果。其中，空心方块即为我们要预测的点，颜色代表所处类别，红色为类别$0$，蓝色为类别$1$，可见，我们对于这个三个点的预测正确。

图4

---

附录：

这里我们给出图1-图4的Python源代码

图1：

# -*- coding: utf-8 -*-
# @Time : 2020/4/12 14:52
# @Author : tengweitw

import numpy as np
import matplotlib.pyplot as plt

# Set the format of labels
def LabelFormat(plt):
    ax = plt.gca()
    plt.tick_params(labelsize=14)
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    font = {'family': 'Times New Roman',
            'weight': 'normal',
            'size': 16,
            }
    return font

x=np.linspace(-10,10,100)
y=1/(1+np.exp(-x))

x_train0=np.array([-10,-7.5,-5])
y_train0=np.array([0,0,0])
x_train1=np.array([5,7.5,10])
y_train1=np.array([1,1,1])

plt.figure()


p1,=plt.plot(x,y,'k-')
p2,=plt.plot([-7.5,7.5],[0,1],'k--')
p3=plt.scatter(x_train0,y_train0,marker = 'o', color='r')
p4=plt.scatter(x_train1,y_train1,marker = 'D', color='r')

# Set the labels
font = LabelFormat(plt)
plt.xlabel('$x$', font)
plt.ylabel('$\hat y$', font)

plt.yticks([0,0.25,0.5,0.75,1.0])
plt.grid()
l1=plt.legend([p1,p2],['$\hat y=\\frac{1}{1+e^{-x}}$','$\hat y=x$'], loc='upper left',fontsize=16)

l2=plt.legend([p3,p4],['Positive instances','Negative instances'], loc='lower right',fontsize=14, scatterpoints=1)
plt.gca().add_artist(l1)
plt.show()

图2-图4：

# -*- coding: utf-8 -*-
# @Time : 2020/4/13 15:24
# @Author : tengweitw


import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import  datasets

# Create color maps for three types of labels
cmap_light = ListedColormap(['tomato', 'limegreen', 'cornflowerblue'])

# Set the format of labels
def LabelFormat(plt):
    ax = plt.gca()
    plt.tick_params(labelsize=14)
    labels = ax.get_xticklabels() + ax.get_yticklabels()
    [label.set_fontname('Times New Roman') for label in labels]
    font = {'family': 'Times New Roman',
             'weight': 'normal',
             'size': 16,
             }
    return font

# Plot the training points: different
def PlotTrainPoint(train_data,train_target):

    for i in range(0, len(train_target)):
        if train_target[i] == 0:
            plt.plot(train_data[i][0], train_data[i][1], 'rs', markersize=6, markerfacecolor="r")
        else:
            plt.plot(train_data[i][0], train_data[i][1], 'bs', markersize=6, markerfacecolor="b")


def PlotTestPoint(test_data,test_target,y_predict_test):
    for i in range(0, len(test_target)):
        if test_target[i] == 0:
            plt.plot(test_data[i][0], test_data[i][1], 'rs', markerfacecolor='none', markersize=6)
        else:
            plt.plot(test_data[i][0], test_data[i][1], 'bs', markersize=6, markerfacecolor="none")


def Logistic_regression_gradient_descend(train_data, train_target, test_data, test_target):
    # learning rate
    eta = 1e-3
    M = np.size(train_data, 1)
    N = np.size(train_data, 0)
    w_bar = np.zeros((M + 1, 1))

    # the 1st column is 1 i.e., x_0=1
    temp = np.ones([N, 1])
    # X is a N*(1+M)-dim matrix
    X = np.concatenate((temp, train_data), axis=1)
    train_target = np.mat(train_target).T

    iter = 0
    num_iter = 3000
    E_train = np.zeros((num_iter, 1))

    while iter < num_iter:
        # Predicting training data
        z = np.matmul(X, w_bar)
        y_predict_train = 1 / (1 + np.exp(-z))
        # Update w
        temp = np.matmul(X.T, y_predict_train - train_target)
        w_bar = w_bar - eta * temp

        # Training Error
        E=0
        for i in range(len(train_target)):
            # print(y_predict_train[i])
            E=E-train_target[i]*np.log(y_predict_train[i])-(1-train_target[i])*np.log(1-y_predict_train[i])
        E_train[iter] = E
        iter += 1

    # Predicting
    x0 = np.ones((np.size(test_data, 0), 1))
    test_data1 = np.concatenate((x0, test_data), axis=1)
    y_predict_test_temp = np.matmul(test_data1, w_bar)

    y_predict_test=1/(1+np.exp(-y_predict_test_temp))

    return y_predict_test,E_train,w_bar




# import dataset of iris
iris = datasets.load_iris()

# The first two-dim feature for simplicity
data = iris.data[:, :2]
# The labels
label = iris.target

# Group 2 and 3 as one group, and label them as 1
label[50:]=1

# Choose the 25,75,125th instance as testing points
test_data = [data[25, :], data[75, :], data[125, :]]
test_target = label[[25, 75, 125]]

data = np.delete(data, [25, 75, 125], axis=0)
label = np.delete(label, [25, 75, 125], axis=0)

train_data = data
train_target = label

y_predict_test,E_train,w_bar=Logistic_regression_gradient_descend(train_data, train_target, test_data, test_target)
print('The probability of being class 1 is: ')
print(y_predict_test)

plt.figure()
plt.plot(E_train, 'r-')
# Set the labels
font = LabelFormat(plt)
plt.xlabel('Iteration', font)
plt.ylabel('Error', font)

plt.show()

plt.figure()
PlotTrainPoint(train_data,train_target)
PlotTestPoint(test_data,test_target,y_predict_test)
font = LabelFormat(plt)
plt.xlabel('$x^{(1)}$', font)
plt.ylabel('$x^{(2)}$', font)
plt.show()