计算机科学导论笔记（十五）

thdwx

于 2023-03-20 18:10:41 发布

阅读量765

点赞数

分类专栏：计算机导论笔记文章标签：计算机科学导论

本文链接：https://blog.csdn.net/thdwx/article/details/129666683

版权

计算机导论笔记专栏收录该内容

15 篇文章 8 订阅

订阅专栏

十七、计算理论

在之前的章节中，我们把计算机看成一台问题求解机器。在这一章中，回答一些诸如此类的问题：哪些问题可以通过计算机解决？语言之间是否存在优劣？运行一个程序前，是否可以确定该程序会停止还是一直运行？

17.1 简单语言

我们可以仅用三条语句来定义一种语言，它们是：递增语句、递减语句和循环语句。在该语言中，只能使用非负整数数据类型。这里不需要其他数据类型，目标仅仅是说明计算理论中的一些思想。该语言只使用少数几个符号。

17.1.1 简单语句的威力

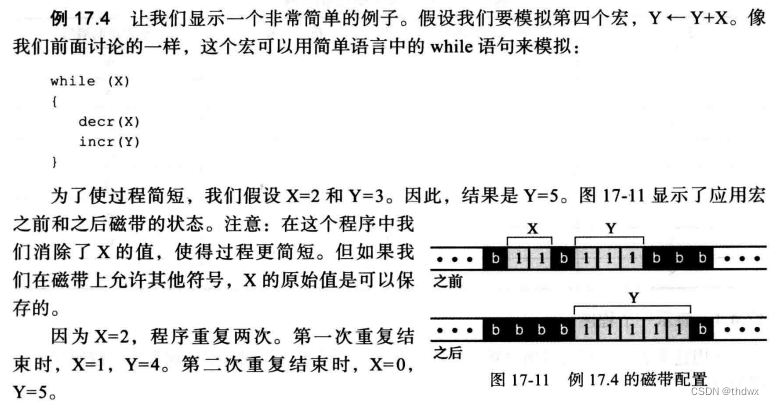
可以证明只使用这三种简单语句的简单程序设计语言和我们现在使用的任何一种复杂语言一样强大（虽然效率上不一定）。下面演示如何模拟当今流行语言中的一些语句。

1. 简单语言中的宏

我们把每次模拟称为一个宏，并且在其他模拟中使用时不需要再重复其代码。一个宏是高级语言中的一条指令，它等价于相同语言中的一条或多条指令的特定集合。

其他宏：显然我们需要更多的宏使简单语言与高级语言相匹配，建立其他宏是可能的，但是并不简单。

2. 输入和输出

在简单语言中，read X 语句可以使用 $X\leftarrow n$ 来模拟，我们也可以模拟输出，即假定程序中使用的最后一个变量保存将要打印的数据。简单语言不是实际语言，而是仅仅用来证明计算机科学中的一些定理。

17.2 图灵机

图灵机是1936年由Alan M. Turing提出用来解决可计算问题的。它是现代计算机的基础。我们将用一个非常简单的版本来说明它是如何工作的。

17.2.1 图灵机的组成部件

图灵机由三部分组成：磁带、控制器和读写头。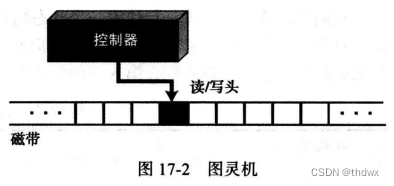

1. 磁带

虽然现代计算机中使用的随机存储设备的容量是有限的，但是我们假定图灵机中的内存是无限的。磁带任何时候只能保存一系列顺序字符，该字符来自计算机所能接收的字符集中。假设图灵机只能接收两个符号：空白（b）和数字1，并且图灵机处理正整数，如下图。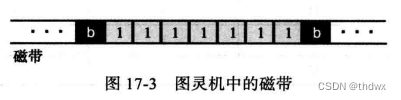

左边的空白定义了存储在磁带上非负整数的开始，一个整数由1构成的串表示（如1111表示整数4）。右手的空白定义了整数的结束。磁带上的为存储数据的其他部分保存了空白。如果磁带上有多个整数，那么它们至少用一个空白字符隔开。

2. 读写头

读写头总是指向磁带上的一个符号，称这个符号为当前符号，读写头每次在磁带上读写一个符号。每读写完一次，它向右移或者向左移或者停止。读写和移动都是在控制器指令下进行的。

3. 控制器

控制器是理论上功能类似于现代计算机的中央处理单元（CPU）的部件，它是一个有限状态自动机，即该机器有预定的有限个状态并能根据输入从一个状态转移到另一个状态，但任何时候它只能处于这些状态中的一种。

下图给出了简单控制器作为有限状态自动机控制器的状态转移图。在这个图中，自动机有三个状态（A、B和C），图中给出了读入字符后引起的状态转移。磁带上的符号只有空白和数字1，所以每个状态出去的路径只有两条：要么读到空白，要么读到1.线（称为转移线）的起点为当前状态，线的末端（箭头）显示的是接下来的状态。

根据上图可以建立一个每一行代表一个状态的状态转移表，并且能够创建这个机器的指令集。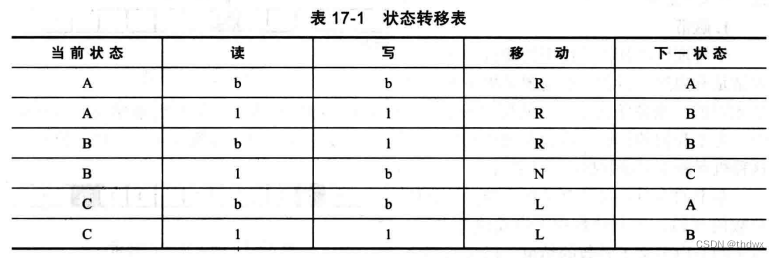

例如，第一条指令是说，当前状态为A，当读写头读到空白时，写入空白，并向右移到下一个符号上，机器的状态转移到A。

17.2.2 对简单语言的模拟

我们现在能根据上面描述的图灵机编写指令来实现简单语言的语句了。

1. 递增语句

下图显示了递增语句的图灵机。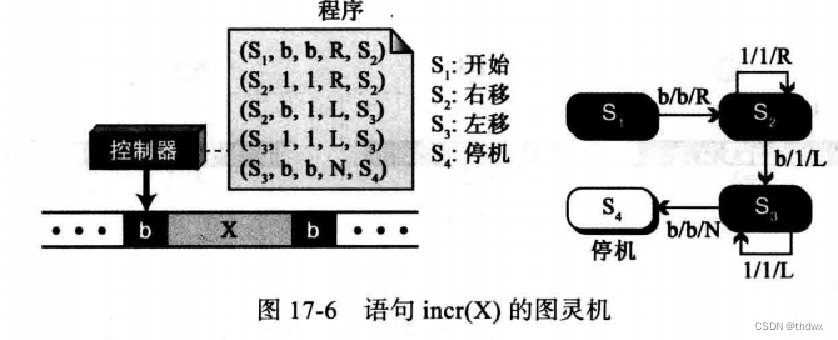

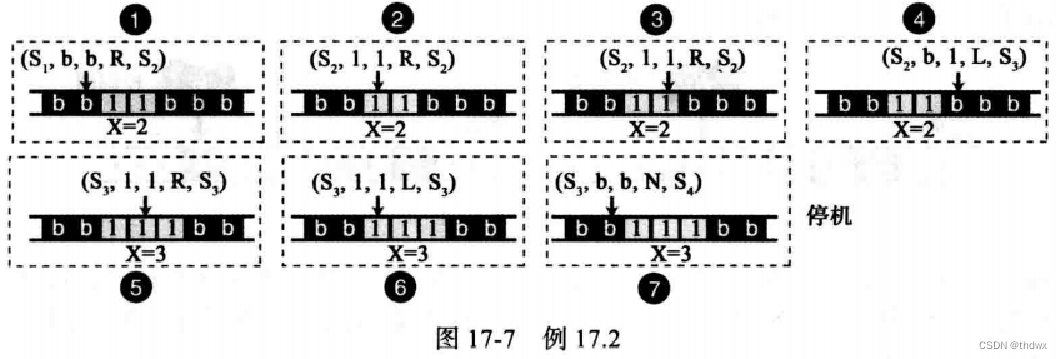
2. 递减语句

下图显示了递减语句的图灵机，在递减语句的实现中，需要有一个检查状态来检查磁带上的数据是否为0.

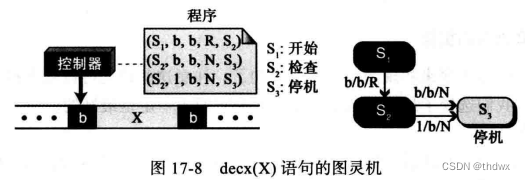
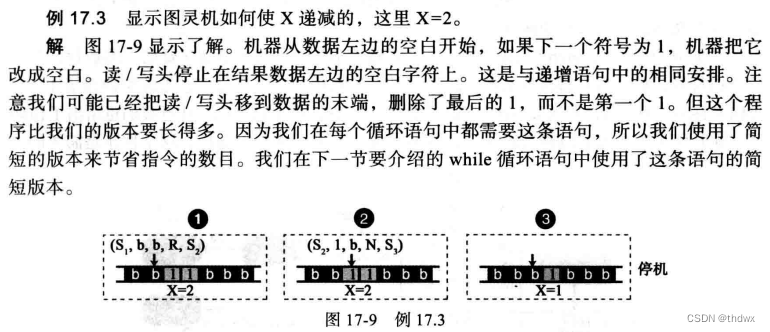
3. 循环语句

为了模拟循环语句，我们假定判断条件X和循环体处理的数据都在磁带上，并且中间有一个空白间隔。

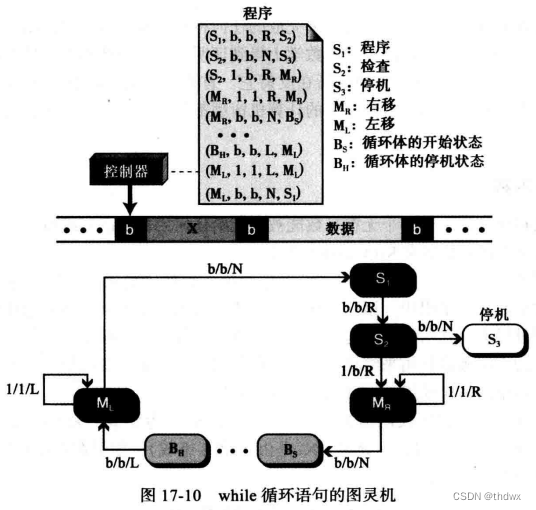
$M_{R}$ 在每次循环中将读写头移动到定义了数据开始位置的空白， $M_{L}$ 在每次数据处理后将读写头移动到定义了X开始位置的空白处。 $B_{S}$ 和 $B_{H}$ 中间是循环体处理指令。检查状态用于检查X是否为0，如果X为0，那么停机（退出循环）。

17.2.3 邱奇-图灵论题

如果存在一个能完成符号操纵任务（例如上述对空白符号和数字1操纵的算法）的算法，那么也存在一台完成这个任务的图灵机。

基于这样的观点，能用写一个算法来完成的任何任务也可以用图灵机完成。注意，这只是一个论题，并不是定理。定理可以在数学上得到证明，论题不能。但是现在有越来越多的证据都可以支持这个论题。首先，尚未发现有图灵机不能模拟的算法；其次，所有在数学上得到证明的计算机模型都与图灵机模型等价。

17.3 哥德尔数

在计算机科学理论中，一个无符号整数能被分配给任何用特定语言编写的程序，这个无符号整数通常称为哥德尔数。

这种分配有很多优点。首先，程序可以作为单一数据项输入给其他程序；其次，程序可以通过它的整数表示来引用；最后，该编号方式可以用来证明有一些问题计算机并不能解决，从而说明世界上的问题数量远远比编写的程序数量要多。

我们用一个简单的变换给简单程序语言编写的程序编号，假定简单语言仅使用15个标志符。

在这种语言中仅使用 $X_{1},X_{2},...,X_{9}$ 作为变量.为了将变量编码，将它看成是由 $X$ 和数字组成的两部分。

17.3.1 表示一个程序

运用这个表，我们可以通过唯一的正整数表示用简单语言编写的任何程序。按照以下步骤进行：

1. 将一个符号用表中所给的对应十六进制代码代替；

2. 将最后的结果（十六进制）转化为无符号整数。

17.3.2 翻译一个数字

为了证明编号方式是唯一的，用以下步骤来解释哥德尔数：

1. 将数字转换成十六进制数；

2. 根据表将每个十六进制数翻译成对应的符号（忽略0）。

虽然用简单语言编写的一切程序都能用数字表示，但是并不是所有的数字都能解释为合法程序。转换之后，如果符号不符合语法规则，这个数字就不是有效的程序。

17.4 停机问题

几乎所有的简单语言编写的程序都包含某种形式的重复（循环或递归函数）。一个重复结构可能永远都不会结束（停机）。这就引出了一个问题：我们能编写一个程序来测试任何可以用哥德尔数表示的程序是否会终止吗？现在已经证明这样的程序是不可能存在的。

17.4.1 停机问题是不可解的

1. 证明

下面给出一个测试程序不存在的非正式的证明。在这个过程中，使用了反证法。

第一步：假设存在一个测试程序，它能接收任何其他程序作为输入，当其他程序能终止，测试程序输出1，否则输出0.

第二步：我们创建另外一个程序，叫strange，它由两部分组成：测试程序和一个循环。当输入程序会终止，测试程序输出1，那么循环不会终止，也就是说strange不会终止；反之，输入程序不会终止，则strange会终止。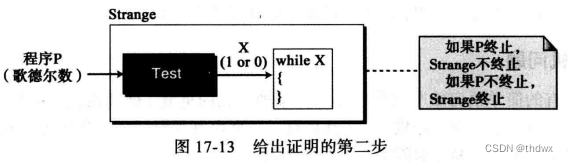

第三步：我们使用strange程序作为strange程序的输入，这是合法的，因为我们没有对输入程序做任何限制。书中这里描述的并不是很清楚，因为作为输入的strange也需要一个输入，否则这两个strange程序就不能当作同一个程序了（一个有输入一个无输入）。我的理解是，这是一个无限的递归过程，输入strange程序的输入是另一个strange程序（这个strange程序的输入又是一个strang程序），那么在这整个环节中，任取一个strange程序都与它的输入或是它输入的程序都是等价的。所以在这种情况下，矛盾就产生了。

2. 矛盾

假设测试程序存在，我们就得到了如下矛盾：

如果strange程序终止，那么strange程序不终止；

如果strange程序不终止，那么strange程序终止。

由反证法就可以得到测试程序不存在，也就是说：停机问题是不可解的。

停机问题的不可解性已经证明了许多其他问题是不可解的，因为如果它们可解，那么停机问题也可解，但停机问题不可解。

17.5 问题的复杂度

在计算机科学领域，一般来说问题可以分为两类：可解问题和不可解问题。可解问题又分为两类：多项式问题和非多项式问题。

17.5.1 不可解问题

要证明一个问题是无法解决的，方法是证明如果它可以解决，那么停机问题也可以解决，换句话说，证明一个问题无法解决就是要将它转化为停机问题。

17.5.2 可解问题

能够被计算机解决的问题无穷无尽，我们关心的是：计算机需要花多长时间去解决一个问题，或者，这个问题有多复杂？

问题的复杂度可以用不同的方法衡量，例如，运行时间、需要的内存等。

1. 可解问题的复杂度

衡量可解问题复杂度的一个方法是找出计算机运行该程序时要执行的运算数量。这样，复杂度问题不是依赖于运行程序的计算机速度，而是依赖于输入的数目。例如，如果程序在处理一个表，则复杂度依赖于该列表中元素的数目。

2. 大O表示法

对于如今计算机的速度，我们关心的是程序总体的数量级而不是精确的数字。例如，如果对两个程序，它们有相同的输入，一个执行15次运算，一次执行25次，它们都运行的很快，以至于看不出什么不同；如果一个执行15次，一个执行10000次，那么它们就有明显区别了。

时间（空间）效率的简化以大O表示法最为著名。这里只给出该表示法的思想并不研究它的定义和计算。在该表示法中，运算数量表示为输入量的函数。符号 $O(n)$ 表示有n个输入，执行n次运算；符号 $O(n^{2})$ 表示有 $n$ 个输入，执行 $n^{2}$ 次运算。

3. 多项式问题

如果程序的复杂度为 $O(logn),O(n),O(n^{2}),O(n^{3}),O(n^{4})$ 或 $O(n^{k}),k$ 为常数，则被称为多项式问题。以如今计算机的处理速度，对于一个有合理输入数量的多项式问题我们都能解决。

4. 非多项式问题

如果一个程序的复杂度远比多项式问题复杂，例如 $O(10^{n})$ 或 $O(n!)$ ，当输入很小时，这种问题可以解决。如果输入很大，则需要花费很长的时间去运算才能看到结果。但随着计算机处理速度的不断提高，我们也许能在更短的时间内解决非多项式问题。

thdwx

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
计算机科学导论笔记（十五）

我的理解是，这是一个无限的递归过程，输入strange程序的输入是另一个strange程序（这个strange程序的输入又是一个strang程序），那么在这整个环节中，任取一个strange程序都与它的输入或是它输入的程序都是等价的。对于如今计算机的速度，我们关心的是程序总体的数量级而不是精确的数字。例如，如果对两个程序，它们有相同的输入，一个执行15次运算，一次执行25次，它们都运行的很快，以至于看不出什么不同；虽然现代计算机中使用的随机存储设备的容量是有限的，但是我们假定图灵机中的内存是无限的。
复制链接

扫一扫