线性回归 Linear Regression

线性回归 Linear Regression

标签：数据挖掘学习

---

1. 什么是线性回归

回归：由一个或一组非随机变量来估计或预测某一个随机变量的观测值时，所建立的数学模型及所进行的统计分析，称为回归分析。

线性回归是一种对数值型的因变量 y (scalar dependent variable)与一个或多个解释变量 X（explanatory variables，或称为自变量）之间的关系，使用线性预测函数来进行建模的回归分析方法。¹

• 只有一个自变量时，称为简单线性回归 simple linear regression
• 有多个自变量时，称为多元线性回归 multiple linear regression

---

2. 简单的例子

假设有一组房价数据，描述了不同面积 $x$（$m^2$）房屋的总价 $y$（万元），如表（共15对数据，表格中省略了其中一部分）：

$x$ ($m^2$)	$y$ (万元)
95	389
68	323
79	340
69	295
…	…
101	461
74	358

x = 95  68  79  69  93  63  75 101  92  57 105  89  74  78  71
y = 389 323 340 295 388 234 355 461 397 269 452 393 358 338 302

我们的问题是，给定一个新的房屋面积 $x^{\prime }$，如何预测其总价 $y^{\prime }$。

在用线性回归来处理该房价预测的问题时，这是一个含有单一自变量的简单线性回归问题。这时我们将面积与总价看做线性相关，假设我们的估价函数为$h(x)$，那么该函数就可以表示为 $h(x)={\theta }_0+{\theta }_{1}x$ 。

2.1 数学表示

线性模型就用 ${\theta }_0$ 和 ${\theta }_1$ 实现了参数化，问题转化为根据样本数据来估计参数，即：

$$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

2.2 损失函数（cost function）

在使用 $h_{\theta }(x)$ 预测房价时，预测值并不一定完全等于真实的房价 $y$，会存在一定的误差 $h_{\theta }(x)-y$，容易想到，越理想的房屋估价函数，其预测结果的误差也越小。

现在我们引入损失函数来量化这个房屋估价函数在样本集上的平均总体误差，：

$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

其中，$m$ 为样本数，$(x^{(i)},y^{(i)})，i=1,2,..,m$ 为每个给定的样本

为使线性函数能够尽可能的拟合样本数据，我们的目标是选取合适的参数${\theta }_0$和 ${\theta }_1$使得误差最小，即损失函数$J$最小。

$$\underset{\theta }{\min }J(\theta )$$

通过损失函数，将参数估计问题，转化为了最优化问题。

• 平方是为了防止正负误差相互抵消，同时二次函数比更高阶的多项式函数简单易处理，而且还是凸函数，求得极小值也就求到了最小值。系数$\frac{1}{2}$是为了求导后方便。
• 不使用绝对值是因为绝对值函数不平滑，可导甚至N阶可导是非常重要的性质，因为转换为最优化问题时，经常不可避免的需要求导。
• 启示：未来我们会遇到很多的假设，在选取函数时，简单、易处理、平滑，这些都是很重要的原则。

3.3 梯度下降法（gradient desent)

现在选取参数 $\theta$ 使 $J_{\theta }$ 最小，在计算机中求解最优化问题通常使用迭代算法，这里引入的是梯度下降法。

梯度下降法：对函数$f(\theta )$，将变量按照梯度下降的方向变化 ${\theta }^{\prime }=\theta -\alpha f^{\prime }(\theta )$，经多次迭代后，最终会走到$f(\theta )$的极值点附近。其中 α > 0 称为步长或者学习速率。其理论依据是，函数沿梯度方向是下降最快。²

对于损失函数，梯度下降法的迭代公式为：
$${\theta }^{\prime }=\theta -\alpha \nabla J_{\theta }$$

其中，${\theta }^{\prime }$和$\theta$是相邻两次迭代的值，$\alpha >0$为常数学习速率，梯度$\nabla J_{\theta }=(\frac{\partial J}{\partial {\theta }_0},\frac{\partial J}{\partial {\theta }_1}{)}^T$

上式也可以写作矩阵的形式：

$$\left(\begin{array}{c}{\theta }_0^{\prime }\\ {\theta }_1^{\prime }\end{array}\right)=\left(\begin{array}{c}{\theta }_0\\ {\theta }_1\end{array}\right)-\alpha \left(\begin{array}{c}\frac{\partial J}{\partial {\theta }_0}\\ \frac{\partial J}{\partial {\theta }_1}\end{array}\right)$$

求解偏导数，根据链式法则：

$$\frac{\partial J_{\theta }}{\partial \theta }=\frac{\partial J_{\theta }}{\partial h_{\theta }}\frac{\partial h_{\theta }}{\partial \theta }=\frac{1}{2m}2\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\frac{\partial h_{\theta }}{\partial \theta }$$

而：

$$\frac{\partial h_{\theta }}{\partial \theta }=\frac{\partial ({\theta }_0+{\theta }_{1}x)}{\partial \theta }=>\{\begin{array}{c}\frac{\partial h_{\theta }}{\partial {\theta }_0}=1\\ \frac{\partial h_{\theta }}{\partial {\theta }_1}=x\end{array}$$

代入上式，可计算出：

$$\{\begin{array}{c}\frac{\partial J}{\partial {\theta }_0}=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})=\frac{1}{m}{\sum }_{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)})\\ \frac{\partial J}{\partial {\theta }_1}=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})x^{(i)}=\frac{1}{m}{\sum }_{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)})x^{(i)}\end{array}$$

得到最终迭代公式：

$$\{\begin{array}{c}{\theta }_0^{\prime }={\theta }_0-\alpha \frac{1}{m}{\sum }_{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)})\\ {\theta }_1^{\prime }={\theta }_1-\alpha \frac{1}{m}{\sum }_{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)})x^{(i)}\end{array}$$

附：生成数据及梯度下降的 R 程序

#!/usr/bin/Rscript
get_gradient <- function(x,y,theta0,theta1) {
    m = length(x)
    s = matrix(0,2,1)
    for (i in 1:m) {
        s[1,1] = s[1,1] + theta0 + theta1 * x[i] - y[i]
        s[2,1] = s[2,1] + (theta0 + theta1 * x[i] - y[i]) * x[i]
    }
    return(1/m*s)
}

J <- function(x,y,theta0,theta1){
    m = length(x)
    s = 0
    for (i in 1:m){
        s = s + (theta0 + theta1 * x[i] - y[i])^2
    }
    return(1/(2*m)*s)
}

x = c(round(runif(15,min=50,max=105)))
noise <- rnorm(15,0,20)
y = c(round(4.5*x + 5 + noise))
#x = c(95,68,79,69,93,63,75,101,92,57,105,89,74,78,71)
#y = c(389,323,340,295,388,234,355,461,397,269,452,393,358,338,302)
print(x) #显示样本集-面积
print(y) #显示样本集-售价
alpha = 0.0001  #这个值相对较合适。尝试了多个值，更大的alpha可能会使J过大而不收敛，更小的alpha可能收敛过慢
theta = matrix(1, 2, 1)
for (i in 1:100) { #迭代100次
    gradient = get_gradient(x,y,theta[1,1],theta[2,1])
    theta = theta - alpha * gradient
}
print(theta) #打印参数结果
print(J(x,y,theta[1,1],theta[2,1])) #打印cost funciton的值，可以从该值看出是否收敛

xx <- 40:120
yy <- theta[1,1]+theta[2,1]*xx

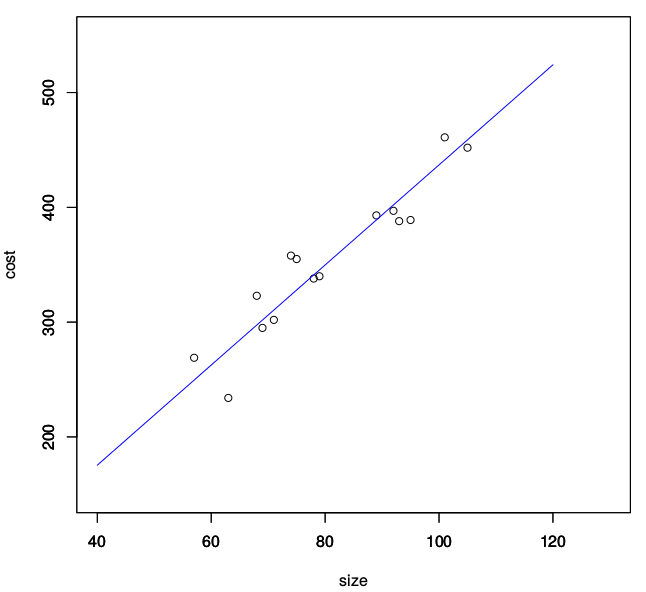
#画图，将散点图和回归直线画在一起
plot(x,y,xlab='size',ylab='cost',xlim=c(40,130),ylim=c(150,550))
par(new=TRUE)
plot(xx,yy,type="l",col="blue",xlab='',ylab='',xlim=c(40,130),ylim=c(150,550))

---

3.一般化的数学模型

上述的简单例子，是单变量的简单线性回归，可以将其推广到多变量的一般情况。

假设有 n 维特征， m 个样本，则：

样本集（m个样本）：

X = ( x ( 1 ) T x ( 2 ) T x ( 3 ) T . . . x ( m ) T ) = ( 1 x 1 (