Codeforces Contest 301D Yaroslav and Divisors —— 树状数组求一段区间内因倍数对数的个数

This way

题意：

给你n个数，m个询问，问你l到r区间内有多少对数互为因倍数：4 2就有3对，4,4和2,2和4,2。

题解：

蛮难想的。
我先处理出从1到每个位置有多少对数。可以从前往后做，也可以从后往前做，我是从后往前做，一开始所有个数可以算出来：
当区间范围是1-n的时候，1的倍数有n个，2的倍数有n/2个。。以此类推加起来
从后往前做的时候枚举每一个当前数的因子和倍数，看看它有没有被删除，没有被删除的话，前面一个位置的答案就-1。
之后我们按询问的左边界从小到大排序，这样的话可以保证只做一遍。在数列为1 3 2 4 5的时候，区间为3 4 的时候，我们维护一个pos表示删到哪了，一开始pos=1，发现l=3，>pos，那么我们找出删除1所能影响的所有位置，在树状数组里维护，再找删除3所能影响的所有位置，加入树状数组。那么答案就是

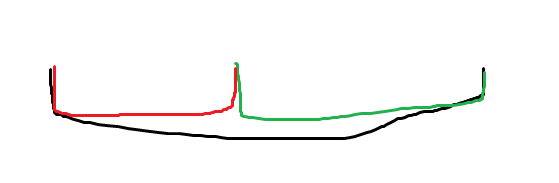
假设我们要查的是绿色的区间，那么就是1到绿色区间结尾的所有可能-1到红色区间结尾的所有可能-红色区间对绿色区间的影响。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+5;
ll pre[N];
int a[N],vis[N],pos[N];
struct node
{
    int l,r,id;
    bool operator< (const node& nod)const
    {
        return l<nod.l;
    }
}q[N];
ll sum[N],ans[N];
int lowbit(int x)
{
    return x&(-x);
}
void add(int x)
{
    for(int i=x;i<N;i+=lowbit(i))
        sum[i]++;
}
int query(int x)
{
    ll ans=0;
    for(int i=x;i;i-=lowbit(i))
        ans+=sum[i];
    return ans;
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    ll sum=n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]),pos[a[i]]=i;
        sum=sum+n/i-1;
    }
    pre[n]=sum;
    for(int i=n;i>=2;i--)
    {
        pre[i-1]=pre[i];
        for(int j=1;j<=sqrt(a[i]);j++)
        {
            if(a[i]%j==0)
            {
                if(!vis[j])
                    pre[i-1]--;
                if(a[i]/j!=j&&!vis[a[i]/j])
                    pre[i-1]--;
            }
        }
        for(int j=2;j*a[i]<=n;j++)
        {
            if(!vis[a[i]*j])
                pre[i-1]--;
        }
        vis[a[i]]=1;
    }
    memset(vis,0,sizeof(vis));
    for(int i=1;i<=m;i++)
        scanf("%d%d",&q[i].l,&q[i].r),q[i].id=i;
    sort(q+1,q+1+m);
    int p=1;
    for(int i=1;i<=m;i++)
    {
        while(p<q[i].l)
        {
            for(int j=1;j<=sqrt(a[p]);j++)
            {
                if(a[p]%j==0)
                {
                    if(!vis[j])
                        add(pos[j]);
                    if(a[p]/j!=j&&!vis[a[p]/j])
                        add(pos[a[p]/j]);
                }
            }
            for(int j=2;j*a[p]<=n;j++)
            {
                if(!vis[a[p]*j])
                    add(pos[a[p]*j]);
            }
            vis[a[p]]=1;
            p++;
        }
        ans[q[i].id]=pre[q[i].r]-pre[q[i].l-1]-query(q[i].r)+query(q[i].l-1);
    }
    for(int i=1;i<=m;i++)
        printf("%lld\n",ans[i]);
    return 0;
}