强化学习笔记

第四章

序列建模与概率图模型

序列建模是分析时间序列数据的一种方法，通常用于预测未来的事件。概率图模型是一种表示随机变量及其依赖关系的图形化模型。常见的概率图模型包括贝叶斯网络和马尔可夫随机场。

贝叶斯网络

贝叶斯网络（Bayesian Network）是一种有向无环图（DAG），用于表示随机变量之间的条件依赖关系。它通过节点表示随机变量，通过有向边表示变量之间的依赖关系。贝叶斯网络常用于概率推理和决策分析，能够高效地处理不完全数据和进行预测。

马尔可夫随机场

马尔可夫随机场（Markov Random Field，MRF）是一种无向图模型，用于表示一组随机变量之间的相互依赖关系。它假设每个变量在给定其邻居节点的情况下，与其他所有变量条件独立。

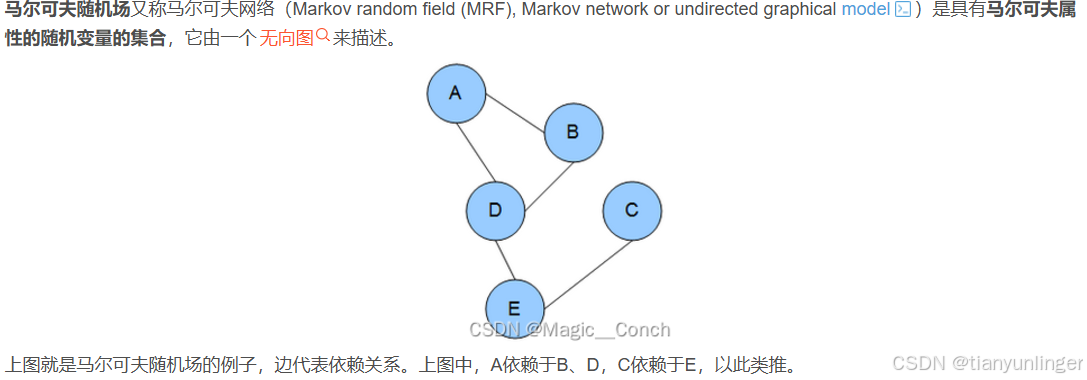
马尔可夫观测过程

马尔可夫观测过程是一种基于马尔可夫链的模型，用于描述系统的状态和观测之间的关系。它假设系统的未来状态只取决于当前状态，与过去的状态无关。

马尔可夫决策过程

马尔可夫决策过程 (MDP) 是一种用于决策优化的数学模型。它通过定义状态、动作、转移概率和奖励来描述一个智能体在环境中如何选择最佳策略。

马尔可夫奖励过程

马尔可夫奖励过程是马尔可夫决策过程的一部分，主要关注在给定状态和动作下的奖励。奖励函数通常用于表示某种效用或代价。

贝尔曼方程

贝尔曼方程是马尔可夫决策过程中的核心公式，用于递归地计算每个状态的价值。它表示当前状态的价值等于即时奖励加上未来状态的期望价值。

$$V(s)=\underset{a}{\max }\left[R(s,a)+\gamma \sum _{s^{\prime }}P(s^{\prime }|s,a)V(s^{\prime })\right]$$

第五章

动态回归（Dynamic Programming）

动态回归（Dynamic Programming, DP）是一种解决复杂问题的方法，通常用于优化问题。它通过将问题分解为子问题，并利用子问题的解来构建原问题的解。动态回归尤其适用于具有重叠子问题和最优子结构性质的问题。

策略迭代（Policy Iteration）

策略迭代是一种求解马尔可夫决策过程（MDP）的算法。它通过不断改进策略来找到最优策略，通常分为两个主要步骤：

策略评估（Policy Evaluation）：给定一个策略，计算每个状态的价值。

策略改进（Policy Improvement）：根据当前策略的价值，改进策略，使得新的策略能获得更高的价值。

该过程不断重复，直到策略不再改变，达到最优策略。

价值迭代（Value Iteration）

价值迭代是另一种求解马尔可夫决策过程（MDP）的算法。它通过反复更新每个状态的价值，直接找到最优价值函数。主要步骤包括：

值更新（Value Update）：根据贝尔曼方程，更新每个状态的价值。

策略提取（Policy Extraction）：一旦价值函数收敛，从中提取最优策略。

价值迭代通常比策略迭代更简单，但在某些情况下收敛速度较慢。

第六章

蒙特卡罗方法（Monte Carlo Methods）

这种方法基于随机采样来估计结果。常用于数值积分和优化问题。比如，模拟大量随机样本来估算一个复杂积分的值。

时序差分（Temporal Difference, TD）

这是一种用来评估某个策略的价值的方法。通过比较预测和实际结果的差异来调整估计值。TD方法结合了蒙特卡罗方法和动态规划的优点。

广义策略迭代（Generalized Policy Iteration, GPI）

GPI是指策略评估和策略改进的交替过程。这种方法是很多强化学习算法的基础，通过不断改进策略来优化行为。

Q学习（Q-Learning）

这是一种无模型的强化学习算法，用于找到最佳动作选择策略（即Q函数）。它通过更新Q值来逐步改善策略，不需要环境模型。

SARSA

SARSA也是一种强化学习算法，与Q学习类似。但它更新的是“实际路径”上的Q值，而不是估计最佳路径上的Q值。SARSA的更新规则基于当前状态-动作对、结果状态、结果动作对的五元组（State-Action-Reward-State-Action）。

例子：如果智能体在当前策略下选择了向右移动并获得了奖励，那么SARSA会根据实际向右移动后的状态和下一个实际动作来更新Q值。即使智能体在策略下向右移动，Q学习仍会根据假设最优的未来动作来更新当前Q值，而不一定是实际采取的动作。

第七章

深度Q网络（Deep Q-Network, DQN）

深度Q网络是一种将深度学习与强化学习结合的方法，用于解决复杂的决策问题。以下是DQN的关键点：

1. Q函数：
   Q函数（或动作价值函数）用于评估在给定状态下采取某个动作的价值。传统的Q学习直接更新Q值表，但在高维空间中，维护Q值表变得不可行。

2. 深度神经网络：
   DQN使用深度神经网络来估计Q值。网络的输入是状态，输出是每个可能动作对应的Q值。

3. 经验回放（Experience Replay）：
   DQN使用经验回放机制来提高样本效率和稳定性。在每个时间步，将经历（状态、动作、奖励、下一个状态）存储到经验回放缓冲区。从缓冲区中随机抽取小批量样本用于网络训练。

4. 目标网络（Target Network）：
   为了稳定训练过程，DQN引入了目标网络。这是一个周期性更新的副本网络，用于生成训练目标，从而减少了目标值的快速变化带来的不稳定性。

5. 损失函数：
   DQN的损失函数通常是时序差分误差的平方，如下所示：

$$L(\theta )=\mathbb{E}[(r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime };{\theta }^{-})-Q(s,a;\theta ){)}^2]$$

其中 $(\theta )$ 和$({\theta }^{-})$ 分别是当前网络和目标网络的参数，( r ) 是奖励，( s ) 和 ( s’ ) 是当前状态和下一个状态， ( a ) 和 ( a’ ) 是当前动作和下一个动作。

总结来说，DQN在解决高维决策问题时表现优异，通过结合深度学习和强化学习的优势，有效学习了复杂环境中的策略。

第八章

策略梯度（Policy Gradient）

策略梯度方法是一类直接优化策略（即行为决策规则）的强化学习算法。其核心思想是，通过梯度上升（或下降）的方法来找到一个最优策略，使得在给定环境中的长期累积回报最大化。

核心思想

1. 策略表示：

   • 策略是一种从状态到动作的映射，可以用一个参数化的函数表示，通常用神经网络实现，记作 $\pi (a|s;\theta )$，其中 $\theta$ 是策略的参数。

2. 目标函数：

   • 强化学习的目标是最大化累积回报 $J(\theta )$。策略梯度方法直接对这个目标函数求导，通过调整参数 $\theta$来优化策略。

3. 梯度估计：

   • 利用蒙特卡罗采样或时序差分方法估计梯度，以更新策略参数。

策略梯度原理

策略梯度定理给出了累积回报对策略参数的梯度公式：

$${\nabla }_{\theta }J(\theta )={\mathbb{E}}_{{\pi }_{\theta }}\left[{\nabla }_{\theta }\log {\pi }_{\theta }(a|s)Q^{\pi }(s,a)\right]$$

其中 (Q^\pi(s, a)) 是状态-动作值函数，表示在状态 (s) 下采取动作 (a) 时的预期回报。

蒙特卡罗策略梯度（Monte Carlo Policy Gradient）

蒙特卡罗策略梯度方法（如REINFORCE算法）通过完整的轨迹来估计策略梯度：

1. 采样轨迹：

   • 在策略 ${\pi }_{\theta }$下采样完整的状态-动作-回报轨迹。

2. 估计回报：

   • 对每个状态-动作对，计算从该状态-动作开始的累积回报$G_t$。

3. 更新策略：

   • 根据梯度公式更新策略参数：

$$\theta \leftarrow \theta +\alpha \sum _t{\nabla }_{\theta }\log {\pi }_{\theta }(a_t|s_t)G_t$$

其中 $\alpha$是学习率。

近端策略优化（Proximal Policy Optimization, PPO）

近端策略优化（PPO）是一种先进的策略梯度方法，通过引入一些优化技巧来提高训练的稳定性和效率。

1. 目标函数：
   • PPO引入了一个剪切的目标函数来限制策略更新的幅度：

$$L^{CLIP}(\theta )=\mathbb{E}\left[\min (r_t(\theta ){\hat{A}}_t,\text{clip}(r_t(\theta ),1-ϵ,1+ϵ){\hat{A}}_t)\right]$$

其中$r_t(\theta )=\frac{\pi }{{\pi }_{{\theta }_{\text{old}}}(a_t|s_t)}$