[leetcode 802] Find Eventual Safe States

In a directed graph, we start at some node and every turn, walk along a directed edge of the graph.  If we reach a node that is terminal (that is, it has no outgoing directed edges), we stop.

Now, say our starting node is eventually safe if and only if we must eventually walk to a terminal node.  More specifically, there exists a natural number K so that for any choice of where to walk, we must have stopped at a terminal node in less than K steps.

Which nodes are eventually safe?  Return them as an array in sorted order.

The directed graph has N nodes with labels 0, 1, ..., N-1, where N is the length of graph.  The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph.

Example:
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Here is a diagram of the above graph.

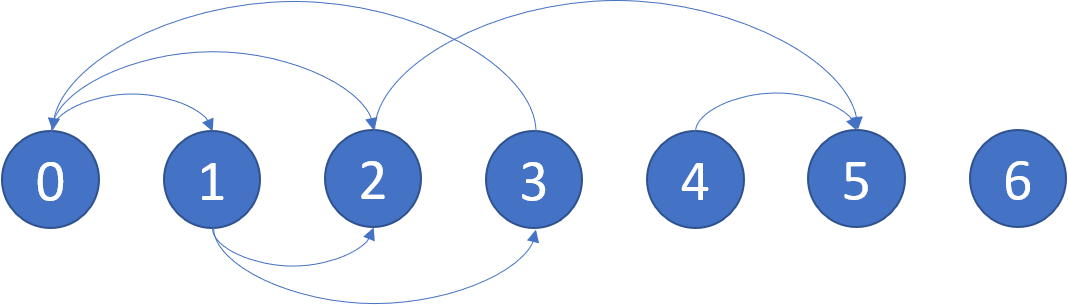
Note:

• graph will have length at most 10000.
• The number of edges in the graph will not exceed 32000.
• Each graph[i] will be a sorted list of different integers, chosen within the range [0, graph.length - 1].

/*
思路：
1）使用 3种不同的color 来表示 node 的状态。0 表示该node 没有被遍历过； 1 表示该node 为安全node；2 表示该node 为不安全node。
2）思路为，
#A, 初始各个node status为0， 当遍历node[i]时，node[i]设为2. 不断DFS node[i]所能够到达的结点。 如果node[i] 能够最终到达安全状态，则设为1.

#B, 依次遍历各个node做为start point。 DFS时，如果发现当前遍历到的node 为1， 则说明后面继续遍历的话，肯定为安全的status， 直接return true。
#C, 如果当前node 为2，则说明继续遍历，出现环， return false。
*/
class Solution {
    public List<Integer> eventualSafeNodes(int[][] graph) {
        List<Integer> res = new ArrayList<>();
        if(graph == null || graph.length == 0)  return res;
        
        int nodeCount = graph.length;
        int[] color = new int[nodeCount];
        
        for(int i = 0;i < nodeCount;i++){
            if(dfs(graph, i, color))    res.add(i);
        }
        
        return res;
    }
    public boolean dfs(int[][] graph, int start, int[] color){
        if(color[start] != 0)   return color[start] == 1;
        
        color[start] = 2;
        for(int newNode : graph[start]){
            if(!dfs(graph, newNode, color))    return false;
        }
        color[start] = 1;
        
        return true;
    }
}

参考： https://leetcode.com/problems/find-eventual-safe-states/discuss/119871/