CPP2022-13-结构体与枚举

已于 2022-11-10 08:15:06 修改
阅读量3.6k 收藏 14
点赞数 5
分类专栏： c++练习及考试 文章标签： c++ 算法 c语言
于 2022-11-09 20:43:03 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/timberman666/article/details/127777312
版权 

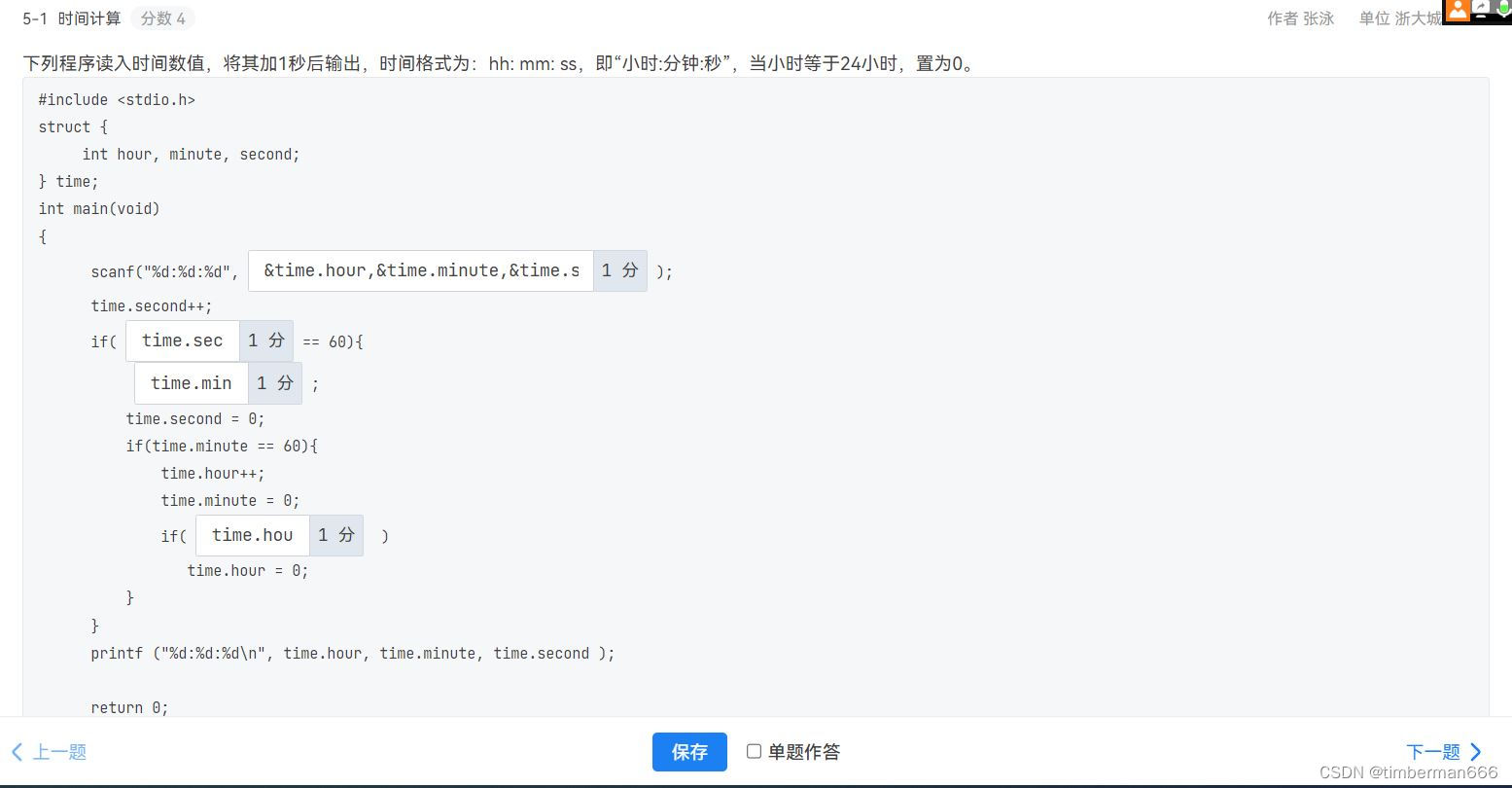
&time.hour,&time.minute,&time.second
time.second
time.minute++
time.hour==24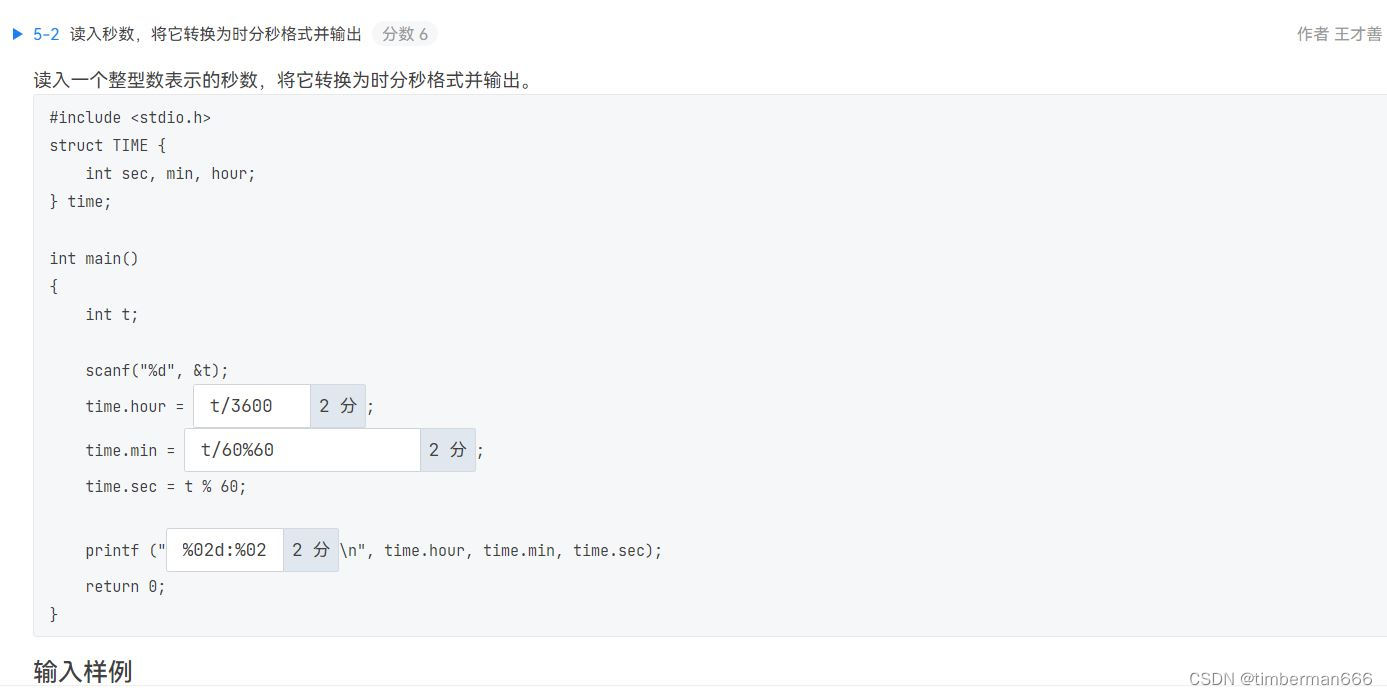

t/3600
t/60%60
%02d:%02d:%02d

6-1 计算两个复数之积

分数 10

全屏浏览题目

切换布局

作者 张泳

单位 浙大城市学院

本题要求实现一个计算复数之积的简单函数。

函数接口定义：

 

struct complex multiply(struct complex x, struct complex y); 
 

其中struct complex是复数结构体，其定义如下：
 

 

struct complex{ int real; int imag; }; 
 

裁判测试程序样例：
 

 

#include <stdio.h> struct complex{ int real; int imag; }; struct complex multiply(struct complex x, struct complex y); int main() { struct complex product, x, y; scanf("%d%d%d%d", &x.real, &x.imag, &y.real, &y.imag); product = multiply(x, y); printf("(%d+%di) * (%d+%di) = %d + %di\n", x.real, x.imag, y.real, y.imag, product.real, product.imag); return 0; } /* 你的代码将被嵌在这里 */ 
 

输入样例：
 

3 4 5 6

 

输出样例：
 

(3+4i) * (5+6i) = -9 + 38i
 

struct complex multiply(struct complex x, struct complex y)
{
    int real,imag;
    real=x.real*y.real-x.imag*y.imag;
    imag=x.imag*y.real+x.real*y.imag;
    struct complex ans={real,imag};
    return ans;
}

 

 

6-2 空间两点间的距离
 

分数 5
 

 

全屏浏览题目
 

 

切换布局
 

作者 庄波
 

单位 滨州学院
 

已知空间中两点 A(x1​,y1​,z1​) 和 B(x2​,y2​,z2​) 之间的欧氏距离定义为：(x1​−x2​)2+(y1​−y2​)2+(z1​−z2​)2​。
 

本题要求实现一个函数，计算平面上两点之间的欧氏距离，平面上点的坐标通过以下结构给出：
 

 

struct point { double x, y, z; }; 
 

函数接口定义：
 

 

// 计算并返回平面上两点 a 和 b 之间的欧氏距离 double distance(struct point a, struct point b); 
 

裁判测试程序样例：
 

 

#include <stdio.h> #include <math.h> struct point { double x, y, z; }; void read_point(struct point *p); double distance(struct point a, struct point b); int main(void) { struct point p1, p2; read_point(&p1); read_point(&p2); printf("%f\n", distance(p1, p2)); return 0; } void read_point(struct point *p) { scanf("%lf %lf %lf", &p->x, &p->y, &p->z); } /* 请在这里填写答案 */ 
 

输入样例：
 

在这里给出一组输入。例如：
 

0 0 0 3 0 4

 

输出样例：
 

在这里给出相应的输出。例如：
 

5.000000
 

double distance(struct point a, struct point b)
{
    double ans;
    ans=sqrt(pow(a.x-b.x,2)+pow(a.y-b.y,2)+pow(a.z-b.z,2));
    return ans;
}

 

 

7-1 复数运算
 

分数 5
 

 

全屏浏览题目
 

 

切换布局
 

作者 李军
 

单位 陕西理工大学
 

复数是由两个实数分别作为实部和虚部构成的一个复合数，从另一个角度来说复数就是由两个实数构成的有序对，在C语言中适合用结构类型来表示复数。现在要求用结构类型
 

 

typedef struct { float x; float y; } Comp; 
 

及其变量来表示与存储复数，编写程序实现复数的加减法运算。
 

输入格式:
 

在一行输入四个用空格分开的实数a1 b1 a2 b2分别表示复数c1 = a1 + b1i和c2 = a2 + b2i
 

输出格式:
 

复数的输出应符合数学上关于复数的表示习惯：实部与虚部都为零时只输出一个0.00； 有一个为零时，只输出非零的部分; 虚部为负时，例如3-4i，应输出为3.00-4.00i的形式，不要输出为3.00+-4.00i。实部与虚部均保留2位小数，例如3.00-4.00i
 输出在两行进行，第一行输出求和的结果，第二行输出求差的结果。
 

输入样例:
 

5.00 4.00 3.00 2.00

 

输出样例:
 

8.00+6.00i
2.00+2.00i
 

#include<bits/stdc++.h>
using namespace std;
struct complex_om
{
    double x;
    double y;
}com[2];
int main()
{
    double x1,y1,x2,y2;
    cin>>x1>>y1>>x2>>y2;
    com[0].x=x1+x2;
    com[0].y=y1+y2;
    com[1].x=x1-x2;
    com[1].y=y1-y2;
    for(int i=0;i<2;i++)
    {
        if(com[i].x==0&&com[i].y==0)
        {
            cout<<0.00<<endl;
        }
        else if(com[i].x==0)
        {
            cout<<fixed<<setprecision(2)<<com[i].y<<"i"<<endl;
        }
        else if(com[i].y==0)
        {
            cout<<fixed<<setprecision(2)<<com[i].x<<endl;
        }
        else if(com[i].y<0)
        {
            cout<<fixed<<setprecision(2)<<com[i].x<<fixed<<setprecision(2)<<com[i].y<<"i"<<endl;
        }
        else
        {
            cout<<fixed<<setprecision(2)<<com[i].x<<"+"<<fixed<<setprecision(2)<<com[i].y<<"i"<<endl;
        }
    }
    return 0;
}
 

 

7-2 结构体应用：计算总分及最高分
 

分数 10
 

 

全屏浏览题目
 

 

切换布局
 

作者 ww
 

单位 中国计量大学现代科技学院
 

本题目要求先输入正整数N，然后输入N个类型为结构体stud的数组元素，计算每个学生的总分，输出每个学生的学号、姓名、三门课的成绩及总分；计算全部成绩的平均分并输出；输出总分最高同学的各项信息。
 struct stud {
 int num; //学号
 char name[10]; //姓名
 int score[3]; //3门课成绩
 int sum; //总分
 };
 

输入格式:
 

先输入不超过10的一个正整数N，然后每行输入一个学生的信息（学号、姓名、三门课成绩）。学号在整数范围内，姓名长度小于10个字符。
 

输出格式:
 

首先输出每个学生的信息（包括学号、姓名、三门课成绩、总分），数据项之间空1格，每人一行；再输出全部成绩的平均分；最后输出总分最高（假设没有相同总分）同学的学号、姓名、三门课成绩及总分，数据项之间空1格。
 

输入样例:
 

在这里给出一组输入。例如：
 

4
1  张三  81  85  82
2  李四  82  78  74
3  王五  85  74  90
4  赵六  77  85  79

 

输出样例:
 

在这里给出相应的输出。例如：
 

1 张三 81 85 82 248
2 李四 82 78 74 234
3 王五 85 74 90 249
4 赵六 77 85 79 241
总平均分=81.000000
3 王五 85 74 90 249
 

#include<bits/stdc++.h>
using namespace std;
struct student
{
    int num;
    string name;
    int score[3];
    int sum;
};
int main()
{
    int sum_all=0;
    int n,max=-1;
    cin>>n;
    struct student information[100];
    for(int i=0;i<n;i++)
    {
        cin>>information[i].num>>information[i].name>>information[i].score[0]>>information[i].score[1]>>information[i].score[2];
        information[i].sum=information[i].score[0]+information[i].score[1]+information[i].score[2];
    }
    for(int i=0;i<n;i++)
    {
        cout<<information[i].num<<" "<<information[i].name<<" "<<information[i].score[0]<<" "<<information[i].score[1]<<" "<<information[i].score[2]<<" "<<information[i].sum<<endl;
    }
    for(int i=0;i<n;i++)
    {
        sum_all=sum_all+information[i].sum;
        if(information[max].sum<information[i].sum)
        {
            max=i;
        }
    }
    double avg;
    avg=(double)sum_all/(3*n);
    cout<<"总平均分="<<fixed<<setprecision(6)<<avg<<endl;
    cout<<information[max].num<<" "<<information[max].name<<" "<<information[max].score[0]<<" "<<information[max].score[1]<<" "<<information[max].score[2]<<" "<<information[max].sum;
}
 

 

7-3 2021-结构体-circle
 

分数 5
 

 

全屏浏览题目
 

 

切换布局
 

作者 gl
 

单位 西南石油大学
 

定义一个结构体类型表示一个圆（x,y,r），圆心坐标是(x,y)，圆半径是r。从键盘输入一个圆的圆心坐标和半径，坐标值和半径均为整型数据，输出这个圆的面积，面积为float。面积公式为area=3.14∗r∗r.
 

输入格式:
 

从键盘输入圆的圆心坐标和半径，之间用空格分隔
 

输出格式:
 

输出数据保留两位小数。
 

输入样例:
 

在这里给出一组输入。例如：
 

3 4 5

 

输出样例:
 

在这里给出相应的输出。例如：
 

78.50
 

#include<bits/stdc++.h>
using namespace std;
struct circle
{
    int x;
    int y;
    int r;
}circle;
int main()
{
    double ans;
    cin>>circle.x>>circle.y>>circle.r;
    ans=3.14*circle.r*circle.r;
    cout<<fixed<<setprecision(2)<<ans;
    return 0;
}
 

 

7-4 寻找最高分
 

分数 5
 

 

全屏浏览题目
 

 

切换布局
 

作者 李军
 

单位 陕西理工大学
 

  给定n(n⩾1)个学生的学号、姓名和3门课的考试成绩。编写程序找出总分最高的学生，并输出其学号、姓名和总分。如果有多个相同的最高分，则输出所有最高分学生的信息。
要求：
   存储学生信息及考试成绩的变量用如下结构类型来定义。
 

struct  Student
{
    char num[11];        //学号，最多10个字符
    char name[11];       //姓名, 最多10个字符
    int s1,s2,s3;        //三门课的考试成绩 
    int total;           //总成绩   
} ;
typedef struct Student Student;  //声明了一个结构类型Student类型

 

输入格式:
 

输入在一行中给出非负整数n(n⩾1)。随后n行，每行给出一个学生的信息，格式为学号 学号 姓名 成绩1 成绩2 成绩3，中间以空格分隔。
要求:
学号、姓名中不包括空白字符(空格、tab符)和空字符串。
 

输出格式:
 

在一行中输出总分最高学生的姓名、学号和总分，间隔一个空格。题目保证这样的学生是唯一的。
 

输入样例:
 

5
2109001 HuangJie 78 83 79
2109002 Liuhaipeng 79 80 77
2109003 Wangqiang 87 86 76
2109004 Liangfeng 92 89 79
2109005 Chengmeng 80 82 75

 

输出样例:
 

在这里给出相应的输出。例如：
 

2109004 Liangfeng 260
 

#include<bits/stdc++.h>
using namespace std;
struct  Student
{
    string num;
    string name;
    int score[3];
    int sum=0;
}student[100];
int main()
{
    int max=0;
    int n;
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>student[i].num>>student[i].name>>student[i].score[0]>>student[i].score[1]>>student[i].score[2];
        student[i].sum=student[i].score[0]+student[i].score[1]+student[i].score[2];
        if(max<student[i].sum)
        {
            max=student[i].sum;
        }
    }
    for(int i=0;i<n;i++)
    {
        if(max==student[i].sum)
        {
            cout<<student[i].num<<" "<<student[i].name<<" "<<student[i].sum<<endl;
        }
    }
    return 0;
}
 

 

7-5 平面向量加法
 

分数 10
 

 

全屏浏览题目
 

 

切换布局
 

作者 乔林
 

单位 清华大学
 

本题要求编写程序，计算两个二维平面向量的和向量。
 

输入格式:
 

输入在一行中按照“x1​ y1​ x2​ y2​”的格式给出两个二维平面向量v1​=(x1​,y1​)和v2​=(x2​,y2​)的分量。
 

输出格式:
 

在一行中按照(x, y)的格式输出和向量，坐标输出小数点后一位（注意不能输出−0.0）。
 

输入样例:
 

3.5 -2.7 -13.9 8.7

 

输出样例:
 

(-10.4, 6.0)
 

#include<bits/stdc++.h>
using namespace std;
struct ans
{
    double x;
    double y;
}ans[2];
int main()
{
    double x,y;
    cin>>ans[0].x>>ans[0].y>>ans[1].x>>ans[1].y;
    x=ans[0].x+ans[1].x;
    y=ans[0].y+ans[1].y;
    if(fabs(x)<=0.05)
    {
        x=0;
    }
    if(fabs(y)<=0.05)
    {
        y=0;
    }
    cout<<"("<<fixed<<setprecision(1)<<x<<", "<<fixed<<setprecision(1)<<y<<")"<<endl;
    return 0;
}
 

7-6 有理数比较
 

分数 10
 

 

全屏浏览题目
 

 

切换布局
 

作者 乔林
 

单位 清华大学
 

本题要求编写程序，比较两个有理数的大小。
 

输入格式：
 

输入在一行中按照“a1/b1 a2/b2”的格式给出两个分数形式的有理数，其中分子和分母全是整形范围内的正整数。
 

输出格式：
 

在一行中按照“a1/b1 关系符 a2/b2”的格式输出两个有理数的关系。其中“>”表示“大于”，“<”表示“小于”，“=”表示“等于”。
 

输入样例1：
 

1/2 3/4

 

输出样例1：
 

1/2 < 3/4

 

输入样例2：
 

6/8 3/4

 

输出样例2：
 

6/8 = 3/4
 

#include<bits/stdc++.h>
using namespace std;
struct ans
{
    int son;
    int mother;
}a[2];
int main()
{
    cin>>a[0].son;
    getchar();
    cin>>a[0].mother;
    cin>>a[1].son;
    getchar();
    cin>>a[1].mother;
    int mother=a[0].mother*a[1].mother/gcd(a[0].mother,a[1].mother);
    int son1=a[0].son*(mother/a[0].mother);
    int son2=a[1].son*(mother/a[1].mother);
    if(son1<son2)
    {
        cout<<a[0].son<<"/"<<a[0].mother<<" < "<<a[1].son<<"/"<<a[1].mother<<endl;
    }
    else if(son1>son2)
    {
        cout<<a[0].son<<"/"<<a[0].mother<<" > "<<a[1].son<<"/"<<a[1].mother<<endl;
    }
    else if(son1==son2)
    {
        cout<<a[0].son<<"/"<<a[0].mother<<" = "<<a[1].son<<"/"<<a[1].mother<<endl;
    }
    return 0;
}
 

7-7 有理数加法
 

分数 10
 

 

全屏浏览题目
 

 

切换布局
 

作者 乔林
 

单位 清华大学
 

本题要求编写程序，计算两个有理数的和。
 

输入格式：
 

输入在一行中按照a1/b1 a2/b2的格式给出两个分数形式的有理数，其中分子和分母全是整形范围内的正整数。
 

输出格式：
 

在一行中按照a/b的格式输出两个有理数的和。注意必须是该有理数的最简分数形式，若分母为1，则只输出分子。
 

输入样例1：
 

1/3 1/6

 

输出样例1：
 

1/2

 

输入样例2：
 

4/3 2/3

 

输出样例2：
 

2
 

#include<bits/stdc++.h>
using namespace std;
struct ans
{
    int son;
    int mother;
}a[2];
int main()
{
    cin>>a[0].son;
    getchar();
    cin>>a[0].mother;
    cin>>a[1].son;
    getchar();
    cin>>a[1].mother;
    int mother=a[0].mother*a[1].mother/gcd(a[0].mother,a[1].mother);
    int son1=a[0].son*(mother/a[0].mother);
    int son2=a[1].son*(mother/a[1].mother);
    int sum_son=son1+son2;
    if(sum_son%mother==0)
    {
        cout<<sum_son/mother<<endl;
    }
    else if(sum_son%mother!=0)
    {
        int g=gcd(sum_son,mother);
        cout<<sum_son/g<<"/"<<mother/g<<endl;
    }
    return 0;
}
 

 
 

7-8 有理数均值
 

分数 10
 

 

全屏浏览题目
 

 

切换布局
 

作者 乔林
 

单位 清华大学
 

本题要求编写程序，计算N个有理数的平均值。
 

输入格式：
 

输入第一行给出正整数N（≤100）；第二行中按照a1/b1 a2/b2 …的格式给出N个分数形式的有理数，其中分子和分母全是整形范围内的整数；如果是负数，则负号一定出现在最前面。
 

输出格式：
 

在一行中按照a/b的格式输出N个有理数的平均值。注意必须是该有理数的最简分数形式，若分母为1，则只输出分子。
 

输入样例1：
 

4
1/2 1/6 3/6 -5/10

 

输出样例1：
 

1/6

 

输入样例2：
 

2
4/3 2/3

 

输出样例2：
 

1
 

#include<bits/stdc++.h>
using namespace std;
int mother;
struct ans
{
    long long int son;
    long long int mother;
};
int main()
{
    long long int mother=1;
    long long int sum_son=0;
    int n;
    cin>>n;
    struct ans a[n];
    for(int i=0;i<n;i++)
    {
        cin>>a[i].son;
        getchar();
        cin>>a[i].mother;
    }
    for(int i=0;i<n;i++)
    {
        mother=mother*a[i].mother/gcd(mother,a[i].mother);
    }
    for(int i=0;i<n;i++)
    {
        sum_son=sum_son+(mother/a[i].mother)*a[i].son;
    }
    if(sum_son%mother==0)
    {
        cout<<sum_son/mother/n<<endl;
    }
    else if(sum_son%mother!=0)
    {
        sum_son=sum_son/n;
        long long int g=gcd(sum_son,mother);
        cout<<sum_son/g<<"/"<<mother/g<<endl;
    }
    return 0;
}
 

 
 

 

7-9 排列枚举
 

分数 10
 

 

全屏浏览题目
 

 

切换布局
 

作者 董卫萍
 

单位 绍兴文理学院元培学院
 

口袋里有红、蓝、黄、黑4种颜色的球若干，每次从口袋先后取出3个球，问得到3种不同颜色的球的可能取法，输出每种排列的情况。球只能是4种颜色之一，而且判断各球是否同色，可以用枚举类型变量处理。
 

输入格式:
 

无
 

输出格式:
 

输出所有排列。
 

输入样例:
 

在这里给出一组输入。例如：
 

无

 

输出样例:
 

在这里给出相应的输出。例如：
 

1 red blue yellow
2 red blue black
3 red yellow blue
4 red yellow black
5 red black blue
6 red black yellow
7 blue red yellow
8 blue red black
9 blue yellow red
10 blue yellow black
11 blue black red
12 blue black yellow
13 yellow red blue
14 yellow red black
15 yellow blue red
16 yellow blue black
17 yellow black red
18 yellow black blue
19 black red blue
20 black red yellow
21 black blue red
22 black blue yellow
23 black yellow red
24 black yellow blue
 

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int count=0;
    enum color{red,blue,yellow,black};
    string color_n[4]={"red","blue","yellow","black"};
    for(int i=red;i<=black;i++)
    {
        for(int j=red;j<=black;j++)
        {
            for(int k=red;k<=black;k++)
            {
                if(i!=j&&i!=k&&j!=k)
                {
                    count++;
                    cout<<count<<" "<<color_n[i]<<" "<<color_n[j]<<" "<<color_n[k]<<endl;
                }
            }
        }
    }
    return 0;
}
 

 

 

 

 

 

 

 

 

 

 

 


                

        

    

  



    



            

  



          




        



    





    



      

      

        
      

      





	

		评论	
	

	
	




  

    

      添加红包
      
    

    

      

        
        

          
          
        

        
请填写红包祝福语或标题

      

      

        
        

          
          个
        

        
红包个数最小为10个

      

      

        
        

          
          元
        

        
红包金额最低5元

      

      

        
        

          当前余额3.43元
          前往充值 >
        

      

      

        

          需支付：10.00元
        

        
        
      

    

  





  

    
    
  

  

    
    
  








  

    

      

        

          

            
            
成就一亿技术人!

          

          

        

        

          

          

            领取后你会自动成为博主和红包主的粉丝
            规则
          

        

      

      

        

          

            
              
            
            

              
hope_wisdom
 发出的红包
            

          

        

        

          

          

          

        

      

    

    

  



      
      

      
实付元

      
使用余额支付

      

        

          

            
            点击重新获取
          

        

        
扫码支付

      

      

        
          
            
          
          
        
      

      

        
        钱包余额
          0
          

            
            

              

                
抵扣说明：

                
 1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
 2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

              

            

          

      

      余额充值