Author:If
转载自:http://www.if-yu.info/2010/10/3/suffix-tree.html
1 Prologue
我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我我是意识流不要读我
俺(If)是不久之前才接触到后缀树这个概念的,而它实在是太迷人了,了解了它的概念之后,我心中曾有过的几个设想顿时都有见到了光明:
比如说, 我希望能做出一个程序,能找出 C 代码中出现次数 × 字串长度最大的 相似 序列,然后帮我#define 一下,好在 POJ 代码长度项上排到第一名;
再比如说, 我还希望做出一个管理自己源代码用的全文检索程序,能够自由的查找含有各种奇特符号的任意代码段 —— 而不是像倒排索引那样事先分好词;
如此这般。
虽然目前为止这些想法都还没有实现,但我已经看到路了。
另外请原谅我这里喜欢使用英文标题 —— 因为 rst2html 会把英文标题的锚点取名为标题本身,这让我看着比较爽一些。
2 Notations
-
T[ j .. i ]
- 字串 T 的 j 到 i 之间的子串。例如 T="hello", 那么 T[ 0 .. 3 ] = "hell"。 T[ j .. i ] 的路径
- T 的子串 T[ j .. i ] 在后缀树中从根节点开始的路径。 STree(T)
- 字符串 T 的后缀树。 “在后缀树中”
- 当我说 “字符串 S 在后缀树中” 时,我的意思其实是后缀树有一条从根节点开始的路径 S 。 阶段,扩展
- 构建后缀树的过程可以分为 n+1 个阶段,其中 n = |T|, 第 i 阶段有 i 次扩展(原始算法),在后面How To Build It 那一节再详细介绍。
3 What is a Suffix Tree
Suffix tree, 或 后缀树 ,是一种相当神奇的数据结构,它包含了字符串中的大量信息,能够用于解决很多复杂的字符串问题 —— 事实上,基本上目前为止俺遇到过的所有与字符串有关的问题都可以通过它解决。
我们以字符串 MISSISSIPPI 为例,先列出它所有的后缀:
1. MISSISSIPPI
2. ISSISSIPPI
3. SSISSIPPI
4. SISSIPPI
5. ISSIPPI
6. SSIPPI
7. SIPPI
8. IPPI
9. PPI
A. PI
B. I
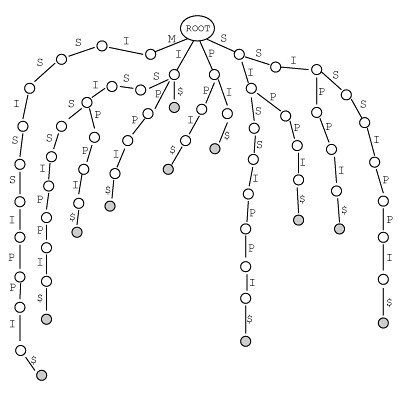
将它们分别插入到 字典树 中我们可以得到:
BTW, 树中的 $ 符号表示字符串结尾 —— 这里 I 是字符串 MISSISSIPPI 的结尾,而 I 又在其中间出现了,所以有必要使用一个特殊的符号标识出来,同理在后缀树中也需要有这样的一个符号;虽然 C 语言中有 '\0' ,但这里使用 $ 符号似乎属于约定俗成的事情了,咱这次也就从了它吧。
这样的一棵字典树已经具备了后缀树的功能 ——
比如说吧,你从根节点开始顺着这个字典树的随便一个树枝走 n 步,然后数一下再往下有几片叶子,就知道已经走过的这 n 个字符组成的字符串在原字符串中一共出现过多少次了 —— 由于你可以把某一节点下方的叶节点数目保存在该节点中,所以这个算法实际上是 O(n) 的,怎么样?
只是,你也看出来了,它的空间复杂度相当之高,实际上基本上没有谁会用这样一个数据结构。
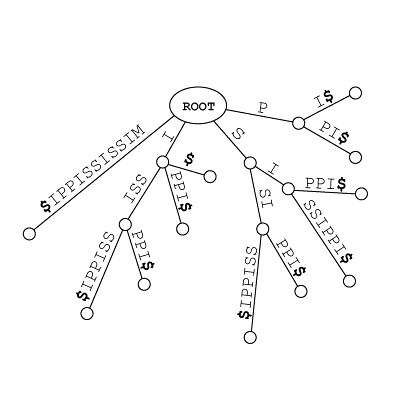
于是, 把所有最近两个有多个分支的节点之间的部分(它们每个节点各自仅有一个分支)合并起来 (参考:Patricia Trie 或曰 Radix Tree),我们可以得到:
这就是一棵后缀树了。
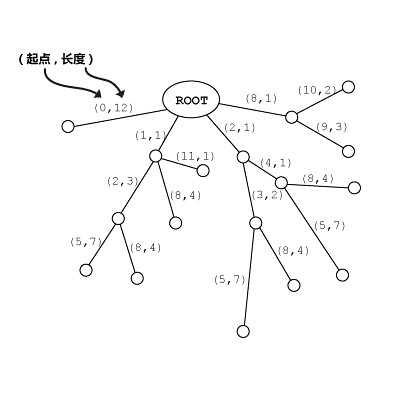
顺便提一句,虽然逻辑结构如上,但实际的数据结构中存储的东西大致是这样的:
这样,每一条边占用的空间为常数大小,于是后缀树 Tree(T) 的空间复杂度为 O(|T|),|T| 为字符串 T 的长度。 因为 :
- 从树根到树叶的每一条路径组成了一个后缀
- 所以树叶的数量等于后缀的数量
- 每个非叶子节点都有至少两条树枝
- 所以非叶节点的数量小于叶节点的数量
- 除去根节点,节点数等于边数
- 所以,后缀树的空间复杂度为: O(|T| + size(edge labels)) [1]
后缀树和 后缀 Trie 一样包含了整个字符串中所有子串的信息,又仅占用 O(|T|) 空间,而且 —— 后面会说到,它可以在 O(|T|) 时间内构造出来,这些特性使它成为了一个理论分析以及实际应用上都非常重要的数据结构。
4 What Can It Do
后缀树的用途是如此之广以至于 Dan Gusfield 在他的书中 [2] 花了七十多页来介绍,我在这里先挑几个自己看来比较好玩的例子说说,以期待激发读者的兴趣。
4.1 Longest Common Substring
Longest common substring - 即 最长公共子串 ,是指在两个字符串中都出现了的最长子串 —— 比如,superiorcalifornialives 和 sealiver 的最长公共子串为 alive 。
这是个很经典的例子,据说 1970 年,后缀树的概念还没有被提出来的时候,Knuth 爷爷曾无比确信找出两个字符串最长公共子串的线性算法是不存在的 [2] ;然而,在知道后缀树的概念之后,这个算法也显而易见了:
- 将两个字符串 T1, T2 加入到同一个后缀树,并在节点上标记该节点属于哪个字符串。
- 遍历后缀树(该后缀树中节点数目不大于 2(|T1|+|T2|),请参照后缀树空间复杂度的证明 ),找出最深的、同时属于两个字符串的节点。
- 从根节点到这个结点的路径就是它们的最长公共子串了。
4.2 Exact String Matching
-
当字符串 T 已知且固定不变,P 改变时:
我们可以用 O(|T|) 时间预处理 T,然后在 O(|P|) 时间内回答出 “P 在 T 中出现了几次?” 或是 “P 在 T 的哪些地方出现过?” 之类的问题:
预处理 T, 得到它的后缀树 —— 也可以把多个字符串 T1, T2 ... 放入同一个后缀树,然后查找 P 时只需要从这个后缀树的根开始顺着 P 往下走,然后读出保存在节点中的信息 (下方的树叶数量、出现地方 &etc.) 就行了。
而这也就意味着你可以把很大的文档进行 索引 ,然后快速的进行搜索。
-
当字符串 P 已知且固定不变时:
我们也可以用 O(|P|) 时间预处理模式串 P,然后用 O(|T|) 时间在 T 中找出 P —— 时间、空间复杂度的上界就和 KMP 算法或是 Boyer-Moore 算法一样。
这个可能看不明显,但是,这么说吧,KMP 算法中 Next 数组保存的所有信息、Boyer-Moore 算法中 Bad-Charactor 和 Good-Suffix 表的信息后缀树中都有。 由于实际操作上比较复杂,这里就不展开了,读者请自行参考 [2] 或者耐心等待 If (嗯,也就是本人) 心血来潮的那一天。
-
当 P 和 T 都已知的时候:
很明显,我们可以在 O(|T| + |P|) 时间内找出 P 在 T 中的出现,不说了。
4.3 Ziv-Lempel Compression
嗯,常说的 LZ77 指的就是 Lempel Ziv 1977。
Ziv-Lempel 压缩的主要思想是,将前方出现过的子串使用 (位置, 长度) 对 表示出来,例如aaaaaaaaaaaaaaaa 就可以表示为 a(1,1)(1,2)(1,4)(1,8) :
a(1,1) == aa
aa(1,2) == aaaa
aaaa(1,4) == aaaaaaaa
aaaaaaaa(1,8) == aaaaaaaaaaaaaaaa
真正的 LZ 编码方式和这里说的有点区别,但思想是一样的。
有了后缀树,LZ 压缩也简单了:
- 对要压缩的字符串 T 构造出后缀树 Tree(T) 。
- 遍历这棵树,在每个节点 v 上标出该节点下方的所有树叶中(位置)最小的值 C(v) 。
- 当需要知道位置 i 上的 (位置, 长度) 编码时:
- 顺着字符串 T[ i..m ] 的前缀走到 p 点。
- 设 v 是 p 下方的第一个节点(或者 p 本身,如果 p 是节点的话)。
- 设 d 是 p 的深度。
- 找出满足 d + C(v) <= i , d 尽可能大的 p 点,则此时从根节点到 p 的路径就是最长的、同时出现在了 T[ 1..i ] 中的 T[ i..m ] 的前缀。
- 即, T[ C(v)..C(v)+d ] == T[ i..i+d ] 。
- 于是, T[ i..i+d ] 就可以表示成 (C(v), d) 序列了。
以上查找 (位置, 长度) 序列的算法时间复杂度是 O(长度),于是压缩算法整体复杂度就是 O(|T|) 。
—— BTW,后面会说到,根据 Ukkonen 的算法 [3] ,后缀树本身可以 "On-line" 构造,即,每次加入一个字符,得到当前的后缀树;这样, Ziv-Lempel 压缩也可以仅用一次自左向右的扫描完成。
5 Few New Concepts
在继续讲如何构造后缀树之前,为了后面表述的方便,再提几个简单的概念:
-
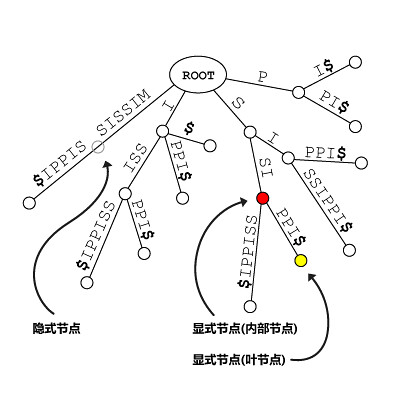
Explicit Node (显式节点) :
- 出现在后缀树里了的所有节点都可以称为 显示节点 。 Internal Node (内部节点) :
- 为了和叶节点区分开来,我们给不是叶节点的显式节点起个新名字,叫做 内部节点 。 Implicit Node (隐式节点) :
- 出现在了 后缀 Trie 中却没有出现在后缀树中的那些节点是 隐式节点 。 显式扩展 :
- 对后缀树做了点什么 隐式扩展 :
- 对后缀树实际上啥都没做
6 How To Build It
目前我只弄懂了 Ukkonen 的算法 [3] ,所以下面也只说这一种算法:
6.1 Native Approach
首先,我们观察发现,若 S 是一个非空字符串, c 是一个字符,则将 c 加到 S 的每个后缀(包括空后缀)后面,我们可以得到 Sc 的所有后缀。
Suffixes(a):
a
Suffixes(ab):
ab
b
Suffixes(abc):
abc
bc
c
Suffixes(abca):
abca
bca
ca
a
...
很显然,可以将这样的原理用于构建后缀树:假设 T[0..i-1] 的后缀树已经建好了,那么在 T[0..i-1] 的每个后缀 T[0..i-1], T[1..i-1] .. T[j..i-1] .. T[i-1..i-1] 的后面加上字符 T[i] 就可以得到 T[0..i] 的后缀树了。
具体到 “将 T[i] 加到后缀 T[j..i-1]” 的这个过程,则有可能遇到三种情况:
- 在后缀树中,T[j..i-1] 停在了树叶上。
这种情况下,只需要把 T[i] 加到该树叶的边上即可。 - 在后缀树中,T[j..i-1] 的后面紧跟着的字符的集合 {a,b,c ... } 中不包含 T[i]。
这种情况下,在 T[j..i-1] 的后面加上树叶 T[i]
(可能需要把隐式节点变换成显式节点)。 - 后缀树中已经有 T[j..i] 了。
这种情况下,我们什么都不用做。
于是,如果不加任何形式的优化,那么 Ukkonen 的算法就是这么回事:
令 n = |T|;
在 T 尾部加上终结符 $。
for i from 0 to n: // n+1 个阶段(包括加上终结符)
for j from 0 to i-1: // 每个阶段 i 次扩展
从后缀树的根顺着 T[ j..i-1 ] 走到节点 v (显式/隐式)
如果 v 下方节点中存在第一个字符为 T[i] 的,则什么都不用做。
否则如果 v 是隐式节点,那么:
将 v 改成显式节点。
在 v 下增加叶节点,从 v 到新节点的边标记为 T[i]。
若 v 是内部节点或根节点:
在 v 下增加叶节点,从 v 到新节点的边标记为 T[i]。
否则: (只能是叶节点了):
将 T[i] 加到边的尾部。
具体的,这里给出构建 MISSISSIPPI$ 的后缀树的全过程,如下:

6.2 Speed Up!
上面的原生态算法虽通俗易懂老少皆宜,但其时间复杂度相当之高 ( O(|T|3) ), 想要有实用价值必须得提高它的效率 —— 而正如前面提到过的,其实后缀树可以在 O(|T|) 时间内构造;这个 O(|T|) 的奇妙算法和上面的算法主体流程其实一样,下面就要介绍加速妙方了,请坐稳。
6.2.1 Stop When T[j..i] Exists
首先说最容易理解的:
很显然,如果后缀树 STree(T[0..i-1]) 中已经存在 T[j..i] 了,那么 T[j+1 .. i] 肯定也在其中, 因为 :
- T[0..i-1] 的所有后缀都在后缀树中。
- T[0..i-1] 的任意子串都可以表示为它的某一个后缀的前缀。
- 所以 T[0..i-1] 的所有子串都在后缀树中。
- T[j+1 .. i] 是 T[j..i] 的子串, T[j..i] 又是 T[0..i-1] 的子串,所以 T[j+1 .. i] 也是 T[0..i-1] 的子串。
- 所以后缀树中存在 T[j+1 .. i] 。
于是乎,碰到 T[j..i] 存在的情况,就不必继续傻乎乎的在树中查找 T[j+1 .. i-1], T[j+2 .. i-1] ... 了。
6.2.2 Opened Leaves
若知道了字符串的长度 l ,又知道了树叶的起点 d ,就可以知道这个树叶的边的长度为 l - d —— 所以首先,不记录树叶的边长并不影响功能。
而如果直接把所有的树叶都标记为开放的,做法例如令其长度为无穷大 —— 这样有一个好处:在对树叶的扩展中就什么都不用做了。
什么时候可以利用这个小技巧呢?我们看看将 T[i] 加入到 STree(T[0 .. i-1]) 的过程:
-
首先, T[0 .. i-1] 肯定停在树叶上。
-
假设 STree(T[0 .. i-1]) 有 n 片树叶,那么 T[1 .. i-1] T[2 .. i-1], T[n-1 .. i-1] 也都会停在树叶上,因为:
对于任何 j < i-1 如果 T[j .. i-1] 不在树叶上,那么 T[j+1 .. i-1] 更不可能在树叶上;
这又是因为, T[j+1 .. i-1] 是 T[j .. i-1] 的后缀,若 T[0 .. i-1] 有子串 S = T[j .. i-1]+'c' (因此 T[j .. i-1] 不在树叶上),那么 T[0 .. i-1] 肯定也有子串 S[1:] = T[j+1 .. i-1]+'c' (因此 T[j+1 .. i-1] 也不在树叶上)。
于是如果 STree(T[0 .. i-1]) 有 n 片树叶,那一定就对应着前 n 个后缀。
所以,已经有了 STree(T[0 .. i-1]) 的话,不必沿着 T[0 .. i-1], T[1 .. i-1] .. T[i-1 .. i-1] 所有这些路径将 T[i] 加入到后缀树;而只需要从 n 开始沿着路径 T[n .. i-1], T[n+1 .. i-1] .. T[i-1 .. i-1] 加入 T[i] 。
6.2.3 Count & Skip
再看从后缀树的根开始查找路径 T[j .. i-1] 的过程,不难发现:
某一条边上进行匹配时,不必一个字符一个字符的比较,而只需要比较第一个字符,跳过剩下来的部分、直接去下一个节点,因为:
- 一个节点每个分支的第一个字符都必定不相等(如果它们相等,则应该被放在上方的边上)。
- 另一方面,在对 STree(T[0 .. i-1]) 进行扩展,即将 T[i] 加到 T[0 .. i-1] 的每一个后缀后时, T[j .. i-1] (0 <= j <= i-1) 已经在树中了,因此顺着 T[j .. i-1] 查找下一次扩展的位置时,不可能遇到某一段边实际不匹配但第一个字符相等的情况。
6.2.4 Suffix Link
好了,接下来要讲最重要也是最难理解的话题:后缀链接了。
6.2.4.1 What is It
用汉语解释 Suffix link 的话,它就是某种显式节点之间的链接,其目的是简化顺着 T[j .. i-1] 找到下一次扩展的地方的过程。
根据 Count & Skip 的技巧,从根节点开始找到扩展点的算法复杂度已经只与下方的分支数有关了,如果能直接从某个很接近扩展点的显式节点开始查找,那么显然能够提高效率。
很巧的,我们发现,如果有某个内部节点的路径为 aS,其中 a 是一个字符、 S 是一个(可能为空的)字符串,那么肯定也会有一个路径为 S 的内部节点、即使没有,也会在下次扩展的时候产生。
因为: 如果 aS 停在一个内部节点上面,也就是 aS 后有分支,那么当前的 T[0 .. i-1] 肯定有子串 aS+c 以及aS+d ( c 和 d 是不同的两个字符) 这两个不同的子串,于是肯定也有 S+c 以及 S+d 两个子串了。至于“下次扩展时产生”的这种情况,则发生在已经有 aS+c 、 S+c ,刚加入 aS+d (于是产生了新的内部节点),正要加入 S+d 的时候。
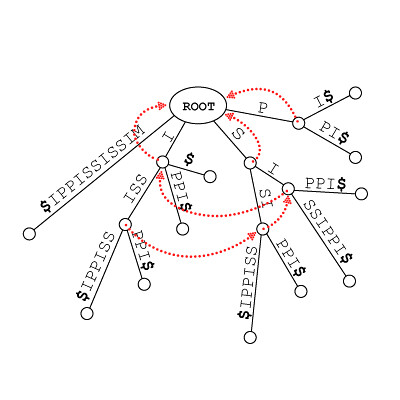
这样,我们将节点 aS 指向 S ,并把这样的一个指向关系称为 aS 的 后缀链接 。
见图中红色箭头:
6.2.4.2 How It Works
后缀链接有什么用呢?
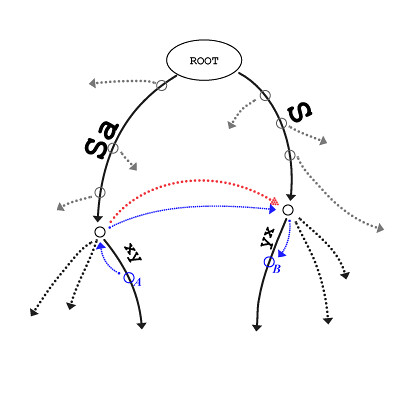
前面似乎提示过了,在 aS 后加上了 d 之后,下一个步骤便是在 S 之后加上 d ;于是同样,在 aSxy 后加上 z (步骤一)之后,下一个步骤是在 Sxy 后加上 z (步骤二)。如果 aS 停在了内部节点上,那么 S 也停在内部节点上,那么从步骤一到步骤二,通过后缀链接,可以直接找到路径为 S 的这个内部节点;然后通过Count & Skip 技巧,可以直接定位到 xy 后方的扩展点。
参考图中 A 节点到 B 节点的蓝色路径:
这里用 MISSISSIPPI 的例子来讲后缀链接似乎不太合适,参考它的构造过程图示,第九步之前树中一直只有一个内部节点,第九步没有利用后缀链接加速,而第九步之后,根据 Opened Leaves 技巧,只需要对 P开头的那一条边进行扩展……但这个例子绝对不意味着后缀链接没有用。
嗯,比如说,作为一个正面的案例,构建 MISSISSIPPIMISSIA 的后缀树的第 17 阶段(加入 'A' ),第 13、14、15 次扩展便是顺着后缀链接进行的( ISSI -> SSI -> SI -> I -> ROOT )。
6.2.4.3 How To Maintain It
那么如何建立和维护后缀链接呢?
依然根据上面提到的原理,我们发现:
在某一阶段中,前一次扩展访问到(或者建立)的内部节点到本次扩展访问到的地方要么已经有了一条后缀链接,要么就应该建立一条后缀链接。
因此,具体实现起来,我们可以保存一个最后访问的内部节点的指针 p ,访问到新的内部节点 node 的时候,将 p 的后缀链接指向 node ,再将 p 设为 node 即可。
6.3 Why O(n)
至于为什么这个算法是线性的,分析起来倒是不难:
设 n = |T|。
- 首先,对于每个阶段的隐式扩展,花费的都是常数时间,因此整体上是 O(n)。
- 然后,每次显式扩展都会产生新的树叶,而整个后缀树中有 n 个树叶;因此显式扩展一共会执行 n 次。 ([2] 中说是 2n 次,为什么?)
- 通过使用 Suffix Link + Count & Skip 技巧,在所有这 n 次显式扩展中,总共的节点访问次数为 O(n) 。这又是因为:
- 假设节点 A 的后缀链接指向节点 B ,A 的路径为 pa , B 的路径为 pb , A 上方有 x 个节点, B 上方有 y 个节点,则有 :
- x <= y + 1 (因为 pb 是 pa 的后缀,因此除了第一个字符之后的分支, pa 路径上的其他分支 pb路径上必然也有,反之则不然)。
- 因此,再看每次显式扩展的过程:从当前位置向下找到扩展点;完成扩展; 向上一个节点;跟随后缀链接来到下一个位置。其中除了“从当前位置向下找到扩展点”这一步之外,剩下的都只需要常数时间。
- 而“向下”查找一次之后,跟随后缀链接来到新的一个节点时最多只能使上方的节点数减少 2。
- 后缀树整体的深度不超过 n ,而总共又只有 n 次显式扩展,因此节点的访问次数为 O(n)
- 因此,显式扩展整体的时间复杂度也是 O(n)。
- 于是,算法的时间复杂度便是 O(n) 了。
6.4 C++ Code
最后,以下代码是我的实现,使用 boost license 以及 GPL v3 发布,需要用的话请自由选择~
使用模板一方面是因为字符的确有不同的类型,另一方面(更主要的)是方便把实现和定义放在同一个文件里,以减少链接的工作(我懒嘛),用 C 的童鞋,对不住了。
本人对下面程序的任何 bug 引起的任何后果不负任何责任,但是如果发现有 bug 请您务必与俺联系。
/*
* File: suffixtree.h
* Author: If
* Created on Sep/14th/2010, 14:02
*
* License: GPL v3 / Boost Software License 1.0
*/
/*
*update: Oct/17th/2010:
Record belongTo information on leaves only,
other works were left to `dfs`, `bfs` and `eachLeaf`
function.
*update: Oct/17th/2010:
Add `eachLeaf` function, for it's quite useful
*/
/*
Permission is hereby granted, free of charge, to any person or organization
obtaining a copy of the software and accompanying documentation covered by
this license (the "Software") to use, reproduce, display, distribute,
execute, and transmit the Software, and to prepare derivative works of the
Software, and to permit third-parties to whom the Software is furnished to
do so, all subject to the following:
The copyright notices in the Software and this entire statement, including
the above license grant, this restriction and the following disclaimer,
must be included in all copies of the Software, in whole or in part, and
all derivative works of the Software, unless such copies or derivative
works are solely in the form of machine-executable object code generated by
a source language processor.
THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE, TITLE AND NON-INFRINGEMENT. IN NO EVENT
SHALL THE COPYRIGHT HOLDERS OR ANYONE DISTRIBUTING THE SOFTWARE BE LIABLE
FOR ANY DAMAGES OR OTHER LIABILITY, WHETHER IN CONTRACT, TORT OR OTHERWISE,
ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER
DEALINGS IN THE SOFTWARE.
*/
/*
Copyright (C) 2010 If
This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation, either version 3 of the License, or
(at your option) any later version.
This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
GNU General Public License for more details.
You should have received a copy of the GNU General Public License
along with this program. If not, see <http://www.gnu.org/licenses/>.
*/
/* following code may cause permanent brain damage, read at your
own risk. */
#ifndef SUFFIXTREE_H
#define SUFFIXTREE_H
// #define HAS_BOOST
#include <functional>
#include <algorithm>
#include <stdexcept>
#include <iterator>
#include <iostream>
#include <vector>
#include <string>
#include <stack>
#include <queue>
#include <assert.h>
#include <stdio.h>
#ifdef HAS_BOOST
#include <boost/pool/object_pool.hpp>
#endif
using std::vector;
using std::basic_string;
#ifdef DEBUG_STREE
FILE* __streeLogFile=stderr;
#define dbg(...) \
do{ \
fprintf(__streeLogFile, __VA_ARGS__); \
fflush(__streeLogFile); \
} while(0)
#define dbg_puts(str, len) \
do{ \
for(int i=0;i<len;++i) \
fputc(str[i], __streeLogFile); \
fflush(__streeLogFile); \
} while(0)
#else
#define dbg(...) /*nothing at all*/
#define dbg_puts(s, l) /*nothing at all*/
#endif
template <class CharT, class Additional=void*>
struct Node
{
// Important members:
CharT const* str; // since edge-node has one-to-one correspondence
int len; // there is no need to separate them.
int startAt; // for the use of presenting an implicit node.
// it will then be the position of first different
// charactor.
Node * link; // suffix link.
Node * parent;
vector<Node*> branches;
int belongTo; // which string does this leaf belongs to.
// *only recorded on leaves*
// Misc members:
int leafNum; // leaf number ( nth suffix ).
int depth; // no need to explain.
Additional info; // some more information you need, depending on
// your application.
Node():
str(0),
len(0),
startAt(0),
link(0),
parent(0),
branches(),
belongTo(-1),
leafNum(0),
depth(0),
info()
{ }
Node(Node const& other):
str(other.str),
len(other.len),
startAt(other.startAt),
link(other.link),
parent(other.parent),
branches(other.branches),
belongTo(other.belongTo),
leafNum(other.leafNum),
depth(other.depth),
info(other.info)
{ }
~Node() { }
/*
static inline int matchFirst(Node const& node, CharT const val){
return node.str[0]==val? node.len : 0;
}
static inline bool ptrMatchFirst(Node const* node, CharT const val){
return node->str[0]==val? node->len : 0;
}
*/
struct MatchFirst {
CharT val;
MatchFirst(CharT v):
val(v)
{ }
inline bool operator()(Node const* node) const {
return node->str[0]==val;
}
};
};
template <class CharT=char, class T=void*>
class SuffixTree
{
protected:
typedef Node<CharT,T> NodeT;
typedef typename vector<NodeT*>::iterator
NodeIterator;
#ifdef HAS_BOOST
boost::object_pool<NodeT>
allNodes_;
#endif
NodeT* root_;
vector<NodeT*> leaves_;
vector<NodeT*> allLeaves_;
int nLeaves_;
vector<basic_string<CharT> >
strings_;
NodeT* latestInternalNode_;
NodeT* currentPos_;
int phase_;
int extension_;
protected:
NodeT* allocNode() {
#ifdef HAS_BOOST
return allNodes_.malloc();
#else
return new NodeT;
#endif
}
void freeNode(NodeT *& node) {
#ifdef HAS_BOOST
allNodes_.free(node);
#else
delete node;
#endif
node = 0;
}
/**
* following str[0:len], and then add str[len] to current tree.
*
* @return true if undone, false if str[0..len] already exists - which means
* extension process is done.
*/
bool extend (CharT const* str, int pos);
// follow path "str" from node down.
NodeT* jumpDown(CharT const* str, int len, NodeT* node, bool fromFront=0);
/**
* split one edge from its startAt position.
*
* @param edge: a node with startAt!=0
* @param leafLabel: label of the newly created leaf, with length==1
* @return newly created leaf.
*/
NodeT* splitEdge(NodeT* edge, CharT const* leafLabel);
void putEnd() {
int p = phase_+1;
int const nth = strings_.size()-1;
for(NodeIterator itr=leaves_.begin(),end=leaves_.end(); itr!=end; ++itr)
{
(*itr)->len = --p - (*itr)->depth;
allLeaves_.push_back(*itr);
}
}
#ifndef HAS_BOOST
inline void destroy(NodeT* node) {
for(NodeIterator itr=node->branches.begin(), end=node->branches.end();
itr!=end; ++itr)
destroy(*itr);
freeNode(node);
}
#endif
private:
SuffixTree(SuffixTree<CharT,T> const&); // complicated while useless,
// i've got no interest.
public:
inline SuffixTree();
inline SuffixTree(basic_string<CharT> const&);
#ifdef HAS_BOOST
~SuffixTree() { /*nothing to do*/ }
#else
~SuffixTree() { destroy(root_); }
#endif
void addString(CharT const * str, int len);
void addString(basic_string<CharT> const& str) {
addString(str.c_str(), str.length()); // to maintain a copy
}
NodeT const* root() {
return root_;
}
/*
void deleteString(CharT const * str, int len);
void deleteString(basic_string<CharT> const& str) {
deleteString(str.c_str(), str.length());
}
*/
// will call f(node) on each node of this tree, including root.
template <class Function>
void dfs(Function f) {
std::stack<NodeT*> todo;
todo.push(root_);
while(!todo.empty()) {
NodeT* node = todo.top();
todo.pop();
for(NodeIterator itr=node->branches.begin(),
end=node->branches.end();
itr!=end;
++itr) {
todo.push(*itr);
}
f(*node);
}
}
// will call f(node) on each node of this tree, including root.
template <class Function>
void bfs(Function f) {
std::queue<NodeT*> todo;
todo.push(root_);
while(!todo.empty()) {
NodeT* node = todo.front();
todo.pop();
for(NodeIterator itr=node->branches.begin(),
end=node->branches.end();
itr!=end;
++itr) {
todo.push(*itr);
}
f(*node);
}
}
template <class Function>
void eachLeaf(Function f) {
for(NodeIterator itr=allLeaves_.begin(), end=allLeaves_.end();
itr!=end; ++itr) {
f(**itr);
}
}
// human-readable json-like format output
void print(std::basic_ostream<CharT> * stream);
// machine-readable dot format output, can be used to
// generate graph using Graphviz
void dot(std::basic_ostream<CharT> * stream);
};
template <class CharT, class T>
SuffixTree<CharT,T>::SuffixTree():
root_(0),
leaves_(),
nLeaves_(0),
strings_(),
latestInternalNode_(0),
currentPos_(0),
phase_(0),
extension_(0)
{
root_ = allocNode();
root_->parent = root_; // for convenience
root_->link = root_;
root_->len = 0;
root_->str = 0;
root_->startAt = 0;
currentPos_ = root_;
}
template <class CharT, class T>
SuffixTree<CharT,T>::SuffixTree(basic_string<CharT> const& str):
root_(0),
leaves_(),
nLeaves_(0),
strings_(),
latestInternalNode_(0),
currentPos_(0),
phase_(0),
extension_(0)
{
root_ = allocNode();
root_->parent = root_; // for convenience
root_->link = root_;
root_->len = 0;
root_->str = 0;
root_->startAt = 0;
currentPos_ = root_;
this->addString(str);
}
template <class CharT, class T>
void SuffixTree<CharT,T>::addString(CharT const* str, int len)
{
strings_.push_back(basic_string<CharT>(str, str+len));
int whichString = strings_.size()-1;
CharT const* cstr = strings_.back().c_str();
dbg("adding string \"%s\" to suffix tree ... \n", cstr);
root_->len = 0;
root_->depth = 0;
leaves_ = vector<NodeT*>();
nLeaves_=0;
currentPos_=root_;
for(phase_=0; phase_<=len; ++phase_) { // there's a '\0' behind
bool undone = true;
latestInternalNode_ = 0;
for(int j=nLeaves_; j <= phase_ && undone; ++j) {
extension_ = j;
undone = extend( cstr+extension_, phase_-extension_ );
}
}
putEnd();
}
template <class CharT, class T>
typename SuffixTree<CharT,T>::NodeT*
SuffixTree<CharT,T>::
jumpDown(CharT const* str, int len, NodeT* node, bool fromFront)
{
dbg("# jumping down path len=%d str=\"", len);
dbg_puts(str,len);
dbg("\" from node %08x ... \n", node);
int i=0;
if(fromFront) {
if (node!=root_ && str[0]!=node->str[0]) {
dbg("!!! cannot find such path !!!\n");
throw(std::runtime_error("path not found"));
}
i = node->len != -1?
node->len:
phase_ - node->depth;
}
for(; i<len; ) {
NodeIterator itr =
std::find_if( node->branches.begin(),
node->branches.end(),
typename NodeT::MatchFirst(str[i]) );
if(itr == node->branches.end()) {
dbg("!!! cannot find such path !!!\n");
throw(std::runtime_error("path not found"));
} else {
dbg("> going into node %08x which begins with \'%c\', len=%d,"
" depth=%d\n",
*itr, (*itr)->str[0], (*itr)->len, (*itr)->depth );
node = *itr;
if( node->len != -1 ) // internal node
i += node->len;
else // leaf
i += phase_ - node->depth;
}
}
if( i != len ) { // implicit node
if(node->len != -1)
node->startAt = node->len - (i-len);
else
node->startAt = phase_ - node->depth - (i-len);
}
dbg("< done.\n");
return node;
}
template <class CharT, class T>
typename SuffixTree<CharT,T>::NodeT*
SuffixTree<CharT,T>::splitEdge(NodeT* node, CharT const* leafLabel /*len==-1*/)
{
/*
*
* \
* # <-- startAt
* \
* node
*
* => => => => => => =>
*
* \
* \
* newInternal
* / \
* / newLeaf (return value)
* node
*
*/
dbg("X spliting edge %08x \n", node);
NodeT* newLeaf = allocNode();
NodeT* newInternal = allocNode();
// newInternal->belongTo = node->belongTo;
newInternal->startAt = 0;
newInternal->len = node->startAt;
newInternal->str = node->str;
newInternal->parent = node->parent;
newInternal->link = root_;
newInternal->depth = node->depth;
newInternal->branches.push_back(node);
newInternal->branches.push_back(newLeaf);
*(std::find(newInternal->parent->branches.begin(),
newInternal->parent->branches.end(),
node)) = newInternal;
node->depth += node->startAt;
node->str += node->startAt;
node->parent = newInternal;
if(node->len != -1) {
node->len -= node->startAt;
}
node->startAt = 0;
newLeaf->str = leafLabel;
newLeaf->depth = node->depth;
newLeaf->link = root_;
newLeaf->len = -1;
newLeaf->parent = newInternal;
dbg(" new internal node = %08x ; \t new leaf = %08x\n",
newInternal, newLeaf);
return newLeaf;
}
template <class CharT, class T>
bool
SuffixTree<CharT,T>::extend(CharT const* str, int pos)
{
dbg("{{{ in phase %d, extension %d;\n", phase_, extension_);
dbg(" adding \'%c\' to suffix tree ... \n", str[pos]);
int const whichString = strings_.size()-1;
int skiped = currentPos_->depth;
NodeT *node = jumpDown(str+skiped, pos-skiped, currentPos_, true);
if (node->startAt != 0) { // implicit node
dbg(" got implicit node %08x starts at %d\n", node, node->startAt);
if(node->str[node->startAt] != str[pos]) {
NodeT *newLeaf = splitEdge( node, str+pos );
newLeaf->leafNum = extension_;
newLeaf->belongTo=whichString;
node = newLeaf->parent;
if(latestInternalNode_) {
latestInternalNode_->link = node;
dbg("-> creating suffix link from %08x to %08x\n",
latestInternalNode_,
node);
}
latestInternalNode_ = node;
currentPos_ = node->parent;
leaves_.push_back(newLeaf);
++nLeaves_;
} else {
dbg(" suffix already exists.\n}}} done.\n");
node->startAt = 0;
return false; // suffix already exists, all done.
}
} else { // explicit node
dbg(" got explicit node\n");
if(latestInternalNode_) {
latestInternalNode_->link = node;
dbg("-> creating suffix link from %08x to %08x\n",
latestInternalNode_,
node);
}
latestInternalNode_ = node;
if( std::find_if( node->branches.begin(),
node->branches.end(),
typename NodeT::MatchFirst(str[pos]) )
!= node->branches.end()) {
dbg(" suffix already exists.\n}}} done.\n");
currentPos_ = node;
return false; // all done.
} else if(node->branches.empty() && node!=root_) {
// a leaf created in the past, now it should be exdended.
node->belongTo=whichString;
node->str = str+pos-node->len;
node->len = -1;
currentPos_ = node->parent;
node->leafNum = extension_;
leaves_.push_back(node);
++nLeaves_;
} else {
// add a leaf to existing explicit node.
NodeT *newLeaf = allocNode();
dbg(" adding new leaf %08x to node %08x.\n", newLeaf, node);
newLeaf->parent = node;
newLeaf->link = root_;
newLeaf->str = str+pos;
newLeaf->len = -1; // leaf
newLeaf->belongTo=whichString;
newLeaf->depth = node->depth + node->len;
node->branches.push_back(newLeaf);
currentPos_ = node;
newLeaf->leafNum = extension_;
leaves_.push_back(newLeaf);
++nLeaves_;
}
}
dbg("-> following suffix link from %08x to %08x ...\n",
currentPos_,
currentPos_->link );
currentPos_ = currentPos_->link;
dbg("}}} done.\n");
return true;
}
static inline char* x08 (char* buf, void const * ptr) {
sprintf(buf, "%08x", ptr);
return buf;
}
template <class CharT, class T>
static void __printSuffixTreeNode(Node<CharT,T>* node,
int margin_left,
int padding_left,
std::basic_ostream<CharT> * stream)
{
int i,I;
char addr[16];
if( node->branches.empty()) {
for(i=0; i<margin_left; ++i)
*stream<<' ';
*stream << '\"';
for(i=0; i<node->len; ++i)
*stream<< node->str[i];
*stream << "\" " << x08(addr, node)
<< "[" << addr << "] ";
*stream << "\n";
} else {
for(i=0; i<margin_left; ++i)
*stream<<' ';
*stream << '\"';
for(i=0; i<node->len; ++i)
*stream<< node->str[i];
*stream << "\" " << x08(addr, node)
<< "[" << addr << "] ";
*stream << ": {\n";
for(i=0, I=node->branches.size(); i<I; ++i) {
__printSuffixTreeNode(node->branches[i],
margin_left+padding_left,
padding_left, stream);
}
for(i=0; i<margin_left; ++i)
*stream<<' ';
*stream << "} \n";
}
}
template <class CharT, class T>
void SuffixTree<CharT,T>::print(std::basic_ostream<CharT> * stream)
{
assert(!"function not supported");
}
template <>
void SuffixTree<char,void*>::print(std::ostream * stream)
// ||
// std::basic_ostream<char>
{
*stream<<"Root ";
__printSuffixTreeNode<char,void*>(root_, 0,2, stream);
}
template <class T>
static void __dotPrintNode(Node<char,T>const*node,std::ostream*stream)
{
char buf[16];
int i,I,j;
for(i=0,I=node->branches.size(); i<I; ++i) {
Node<char,T> const* p = node->branches[i];
*stream<<"node"<<x08(buf,p)<<" [label=\"\"";
if(p->branches.empty())
*stream<<" peripheries=2 width=0.1 height=0.1";
*stream<<"];\nnode"<<x08(buf,node);
*stream<<" -> node"<<x08(buf,p)
<<" [label=\"";
for(j=0;j<p->len;++j)
if(p->str[j])
*stream<<p->str[j];
else
*stream<<"$";
*stream<<"\"];\n";
__dotPrintNode(p,stream);
}
if(!node->branches.empty()) {
*stream<<"node"<<x08(buf,node);
*stream<<" -> node"<<x08(buf, (node->link))<<" "
<<"[color=red];\n";
}
}
template <class CharT, class T>
void SuffixTree<CharT,T>::dot(std::basic_ostream<CharT> *) {
assert(!"function not supported");
}
template <>
void SuffixTree<char,void*>::dot(std::ostream * stream)
{
char buf[16];
*stream<<"digraph stree {\n";
*stream<<"node"<<x08(buf, root_)<<" [label=\"root\"];\n";
*stream<<"node"<<buf<<" -> node"<<buf<<";\n";
*stream<<"node [width=0.2 height=0.2] \n";
__dotPrintNode<void*>(root_, stream);
*stream<<"}\n";
}
#endif /* SUFFIXTREE_H */
// vi:ts=4:foldmethod=marker
7 References
| [1] | : Esko Ukkonen, Suffix tree and suffix array techniques for pattern analysis in strings, Erice School 30 Oct 2005 |
| [2] | (1, 2, 3, 4) : Gusfield, Dan (1999) [1997]. Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology. USA: Cambridge University Press. ISBN 0-521-58519-8 |
| [3] | (1, 2) : E. Ukkonen, On-Line Construction of Suffix Trees, Algorithmica, 14 (1995), 249-260 |






















 273
273

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








