
来源:时序人
本文约2400字,建议阅读9分钟如何评估层级化的时间序列预测模型和算法在现实世界数据集上的稳健性呢?对于层级化的时间序列,普遍的做法是将较低层级的预测值汇总到较的高层级,比如跨国零售销售。目前对预测效果的评估往往局限于一组较小的基准数据集,仅能提供算法行为的片面视角。如何评估层级化的时间序列预测模型和算法在现实世界数据集上的稳健性呢?
来自葡萄牙大学的几位研究者提出了 RHiOTS,他们通过系统地改变现有数据集并修改单个序列及其相互关系的特征来弥补这一空白。RHiOTS 还包含了一个创新的可视化组件,将复杂的多维稳健性评估结果转化为直观、易于解释的可视化图像。
RHiOTS 为研究人员提供了一个全面了解预测算法细微行为的工具,为选择最适合给定问题的方法提供了更可靠的依据。

【论文标题】
RHiOTS: A Framework for Evaluating Hierarchical Time Series Forecasting Algorithms
【论文地址】
https://arxiv.org/abs/2408.03399
【论文源码】
https://github.com/luisroque/robustness_hierarchical_time_series_forecasting_algorithms
论文背景
如何评估层次化时间序列(Hierarchical Time Series, HTS)预测模型和算法的鲁棒性是非常重要的问题。层次化时间序列在多个领域中非常普遍,例如跨国零售销售数据,其中下层级的预测必须累加到上层级。现有的预测方法的实证评估通常限于少数基准数据集,这只能提供对算法行为的有限视角。
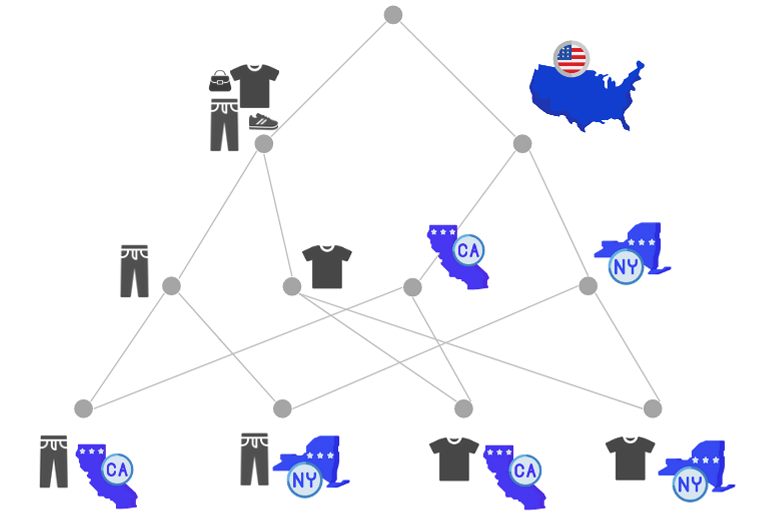
图1:层次化时间序列数据集的简单示例
传统的评估方法无法充分评估 HTS 预测算法在动态场景中的鲁棒性,这些场景中时间序列之间的关系和时间依赖性随时间变化。为了解决这个问题,研究者介绍了一个名为 RHiOTS(Robustness of Hierarchically Organized Time Series)的框架,旨在通过系统地改变现有数据集并修改个体序列及其相互关系的特征,来评估HTS 预测模型和算法在真实世界数据分布变化中的鲁棒性。RHiOTS 使用一系列可参数化的转换来模拟数据分布中的这些变化,并且包含了一个创新的可视化组件,将复杂的多维鲁棒性评估结果转化为直观、易于解释的视觉效果。
研究者对五种不同的 HTS 模型和算法的鲁棒性进行了实证研究,展示了 RHiOTS 作为新评估框架的有用性。
RHiOTS框架方法
01 RHiOTS框架总览
总体来说,RHiOTS 旨在实现两个主要目标:
提供对模型行为的全面理解,通过系统地对数据施加各种转换,然后评估模型的性能来实现这一目标。该过程有助于通过变换和强度来详细评估每个模型的鲁棒性,从而使从业人员能够针对其问题的独特方面和数据属性的潜在变化选择最有效的模型。
支持为特定预测任务选择合适的算法,通过分析不同算法在一系列变换后的数据集上的表现,提供关于哪些算法在不同条件下最具适应性和有效性的见解,这有助于更有效、更明智地比较算法,并提高泛化能力。
RHiOTS 对数据集中的每个个体时间序列应用转换,只对层次结构的叶节点上的时间序列进行转换。在转换后,层次结构的聚合级别会重新计算,即特定组的观察值的总和(或顶级序列)是基于转换后的个体序列计算的。
接下来,RHiOTS 通过将时间序列转换引入的变化与预测性能的变化联系起来,来评估 HTS 预测模型的鲁棒性。为了量化预测性能的变化,文中计算了模型在原始数据集和各种转换版本上预测误差。
02 时间序列转换
RHiOTS 应用基于随机的转换到原始时间序列,这些转换可以影响时间序列的个体组成部分以及数据集中多个时间序列之间的关系。这些转换应该是平滑且连续的,以保持原始和转换序列之间的有意义关系。论文介绍了四种转换:
抖动(Jittering):通过向时间序列的值添加随机噪声分量来定义,噪声的标准差是转换参数。
缩放(Scaling):涉及通过随机标量值修改序列的幅度,缩放因子的标准差定义了转换的参数。
幅度扭曲(Magnitude Warping):通过插值一个立方样条来实现时间序列数据的平滑、连续、非线性转换。
时间扭曲(Time Warping):通过在一组均匀间隔的时间点上插值立方样条来定义,时间扭曲可以拉伸或压缩时间序列的时间轴。
研究者强调,这些转换应该保持原始数据的整体结构和平滑性,以便在转换后的数据集中引入新的动态,同时保留原始数据的基本特征。
实验分析
文中实验的主要目的是展示在 HTS 预测的背景下,RHiOTS 如何用于分析模型和算法的鲁棒性。
文中的实验主要基于7个问题展开分析:
Q1:不同的变换如何影响数据集中时间序列之间的距离
Q2:不同类型的扰动对预测误差的影响
Q3:HTS 预测模型的预测误差如何随时间和序列间依赖性的操纵而变化
Q4:使用 RHiOTS 系统地比较了数据变换对不同算法排名的影响
Q5:使用评估预测性能的基准方法来比较算法的性能
Q6:使用 RHiOTS 来评估时间序列之间依赖性对算法性能的相关性
Q7:确定给定应用领域中最适合的鲁棒算法
文中使用 RHiOTS 进行的实证研究证实,模型和算法的性能会根据应用于数据的扰动而变化,并提供了基于扰动类型的预期效果洞察。
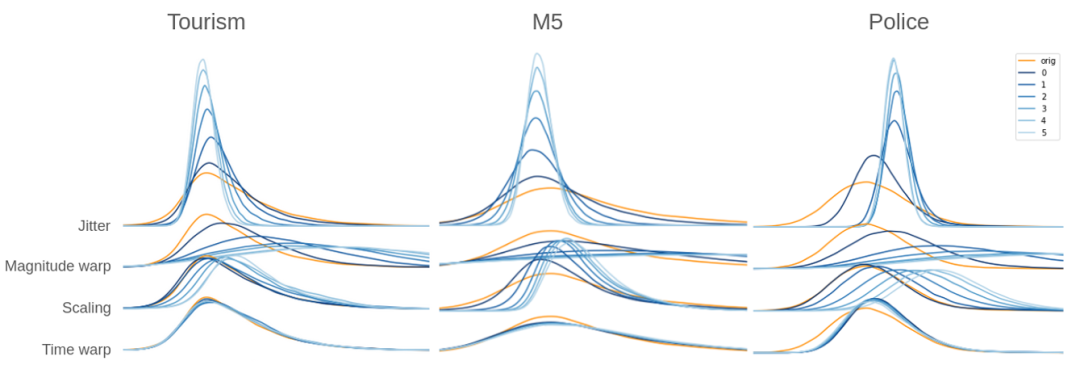
图2:数据集中每个数据集(列)、转换(行)和参数集之间的DTW分布
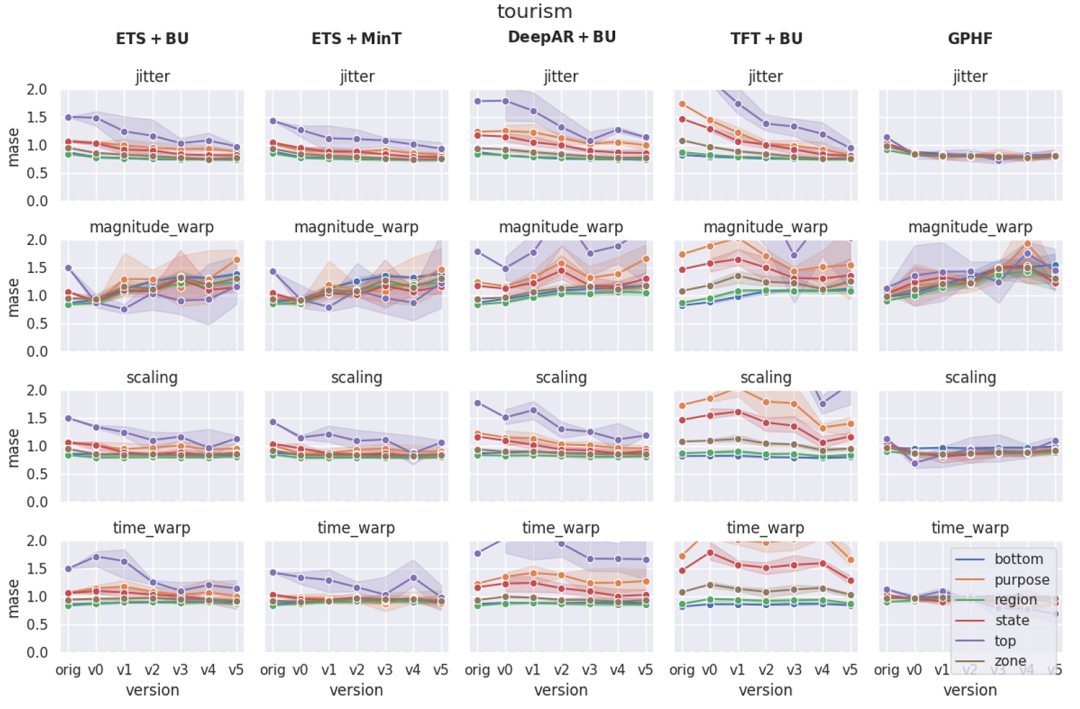
图3:在层次时间序列预测中,使用MASE评估的各种数据变换下的模型性能
首先,实验展示了 RHiOTS 在时间序列之间的相关性方面创建了原始数据集的丰富变化。在评估模型时,预测性能会根据所应用的转换而有很大差异。随着幅度的增加,在幅度扭曲等转换中,性能会迅速下降,而在抖动等情况下则会改善。
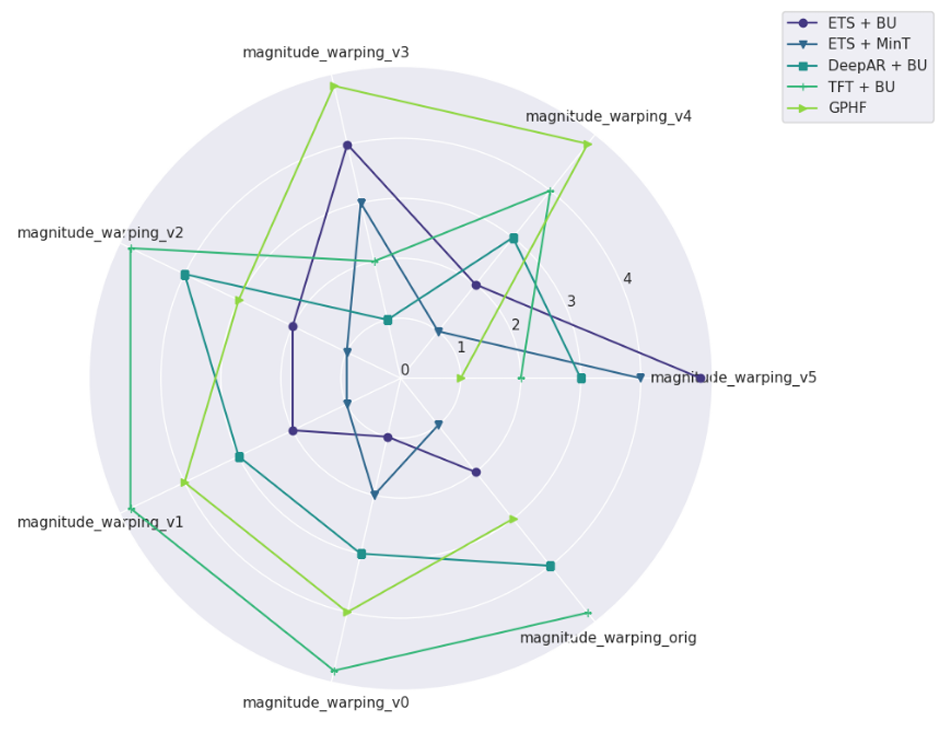
图4:旅游数据集在幅度扭曲变换下,预测方法性能的排名,从原始数据到最强烈的变换
在评估算法时,首先应用传统的基准分析,即比较三个数据集之间的预测性能。由于结果不明确,文中将该方法扩展到使用 RHiOTS。一个收获是,在应用特定的协调方法(如MinT)时,并没有看到鲁棒性方面的有意义差异。
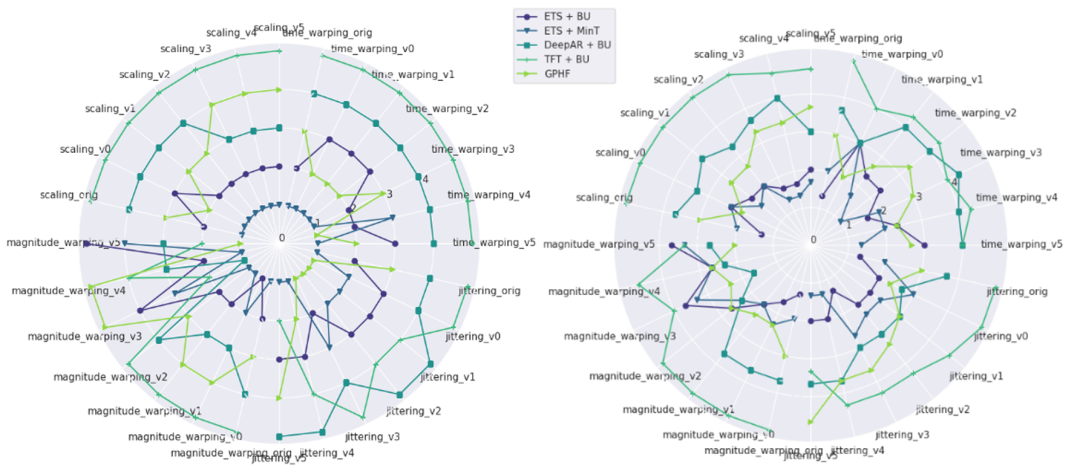
图5:左图为旅游数据集在不同变换下预测算法的性能;右图为所有数据集预测算法性能排名的平均值
第二个是经典算法比更复杂的深度学习算法更鲁棒。深度学习算法仅在转换高度破坏性(如高强度幅度扭曲)时才显示出更强的鲁棒性。
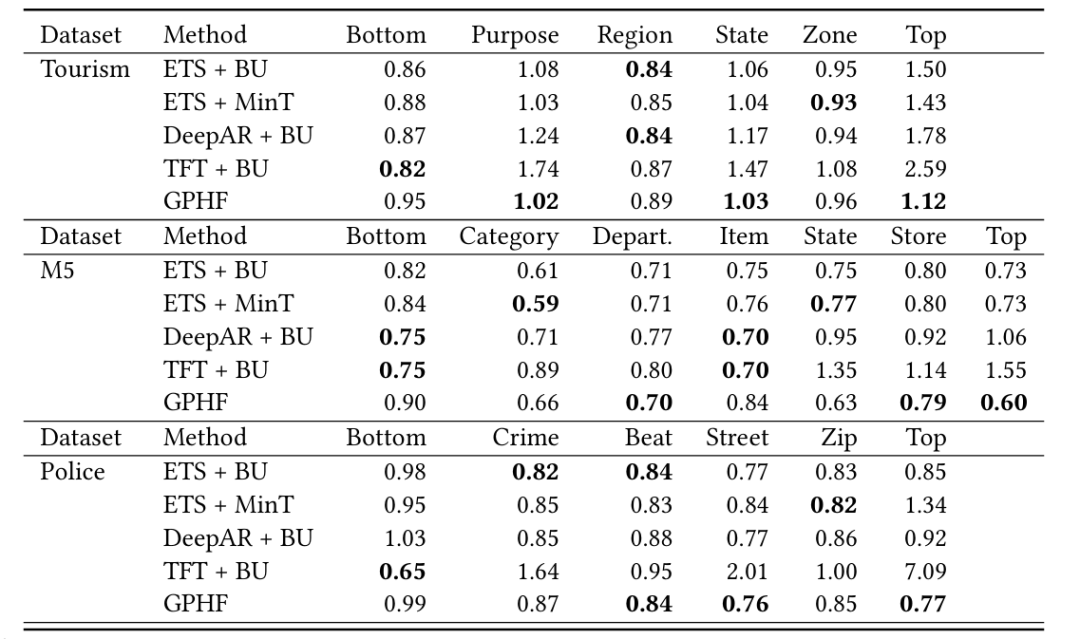
表1:实验中考虑的原始数据集的结果(MASE)
可视化和分析汇总结果表明,如果必须在没有先验知识的情况下从数据集中选择单个模型来避免潜在的失真,那么 ETS 模型是最稳健的选择。
编辑:黄继彦
关于我们
数据派THU作为数据科学类公众号,背靠清华大学大数据研究中心,分享前沿数据科学与大数据技术创新研究动态、持续传播数据科学知识,努力建设数据人才聚集平台、打造中国大数据最强集团军。

新浪微博:@数据派THU
微信视频号:数据派THU
今日头条:数据派THU
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








