I strongly recommend you to read the three articles below first.
Power up C++ with STL: Part I (introduction, vector)
Power up C++ with STL: Part II (string, set, map)
Power up C++ with STL: Part III (more on STL)
Armed with STL, let's go on to the most interesting part of this tutorial: how to implement real algorithms efficiently.
Depth-first search (DFS)
I will not explain the theory of DFS here – instead, read this section of gladius's Introduction to Graphs and Data Structures tutorial – but I will show you how STL can help.
At first, imagine we have an undirected graph. The simplest way to store a graph in STL is to use the lists of vertices adjacent to each vertex. This leads to the vector< vector<int> > W structure, where W[i] is a list of vertices adjacent to i. Let’s verify our graph is connected via DFS:
Notice on for_each: the last argument of this algorithm can be almost anything that “can be called like a function”. It may be not only global function, but also adapters, standard algorithms, and even member functions. In the last case, you will need mem_fun or mem_fun_ref adapters, but we will not touch on those now.
One note on this code: I don't recommend the use of vector<bool>. Although in this particular case it’s quite safe, you're better off not to use it. Use the predefined ‘vi’ (vector<int>). It’s quite OK to assign true and false to int’s in vi. Of course, it requires 8*sizeof(int)=8*4=32 times more memory, but it works well in most cases and is quite fast on TopCoder.
A word on other container types and their usage
Vector is so popular because it's the simplest array container. In most cases you only require the functionality of an array from vector – but, sometimes, you may need a more advanced container.
It is not good practice to begin investigating the full functionality of some STL container during the heat of a Single Round Match. If you are not familiar with the container you are about to use, you'd be better off using vector or map/set. For example, stack can always be implemented via vector, and it’s much faster to act this way if you don’t remember the syntax of stack container.
STL provides the following containers: list, stack, queue, deque, priority_queue. I’ve found list and deque quite useless in SRMs (except, probably, for very special tasks based on these containers). But queue and priority_queue are worth saying a few words about.
Queue
Queue is a data type that has three operations, all in O(1) amortized: add an element to front (to “head”) remove an element from back (from “tail”) get the first unfetched element (“tail”) In other words, queue is the FIFO buffer.
Breadth-first search (BFS)
Again, if you are not familiar with the BFS algorithm, please refer back to this TopCoder tutorial first. Queue is very convenient to use in BFS, as shown below:
There is an interesting application of queue and map when implementing a shortest path search via BFS in a complex graph. Imagine that we have the graph, vertices of which are referenced by some complex object, like:
Priority_Queue
Priority queue is the binary heap. It's the data structure, that can perform three operations:
Dijkstra
In the last part of this tutorial I’ll describe how to efficiently implement Dijktra’s algorithm in sparse graph using STL containers. Please look through this tutorial for information on Dijkstra’s algoritm.
Consider we have a weighted directed graph that is stored as vector< vector< pair<int,int> > > G, where
Many thanks to misof for spending the time to explain to me why the complexity of this algorithm is good despite not removing deprecated entries from the queue.
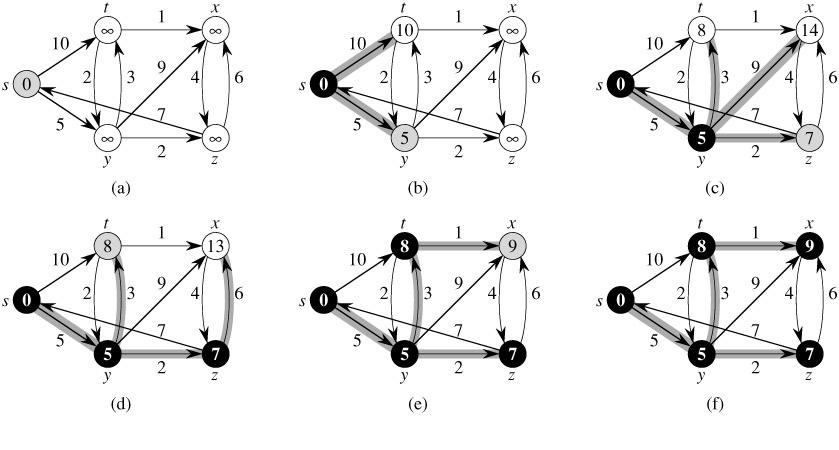
Dijkstra via set
Petr gave me this idea when I asked him about efficient Dijkstra implementation in C#. While implementing Dijkstra we use the priority_queue to add elements to the “vertices being analyzed” queue in O(logN) and fetch in O(log N). But there is a container besides priority_queue that can provide us with this functionality -- it’s ‘set’! I’ve experimented a lot and found that the performance of Dijkstra based on priority_queue and set is the same.
So, here’s the code:
I’ve spent a lot of time to understand why the code that removes elements from queue (with set) works as fast as the first one.
These two implementations have the same complexity and work in the same time. Also, I’ve set up practical experiments and the performance is exactly the same (the difference is about ~%0.1 of time).
As for me, I prefer to implement Dijkstra via ‘set’ because with ‘set’ the logic is simpler to understand, and we don’t need to remember about ‘greater<int>’ predicate overriding.
What is not included in STL
If you have made it this far in the tutorial, I hope you have seen that STL is a very powerful tool, especially for TopCoder SRMs. But before you embrace STL wholeheartedly, keep in mind what is NOT included in it.
First, STL does not have BigInteger-s. If a task in an SRM calls for huge calculations, especially multiplication and division, you have three options:
Nearly the same issue arises with the geometry library. STL does not have geometry support, so you have those same three options again.
The last thing – and sometimes a very annoying thing – is that STL does not have a built-in string splitting function. This is especially annoying, given that this function is included in the default template for C++ in the ExampleBuilder plugin! But actually I’ve found that the use of istringstream(s) in trivial cases and sscanf(s.c_str(), …) in complex cases is sufficient.
Those caveats aside, though, I hope you have found this tutorial useful, and I hope you find the STL a useful addition to your use of C++. Best of luck to you in the Arena!
Note from the author: In both parts of this tutorial I recommend the use of some (macro) templates to minimize the time required to implement something. I must say that this suggestion should always be up to the coder. Aside from whether (macro) templates are a good or bad tactic for SRMs, in everyday life they can become annoying for other people who are trying to understand your code. While I did rely on them for some time, ultimately I reached the decision to stop. I encourage you to weigh the pros and cons of templates and to consider this decision for yourself.
width="728" scrolling="no" height="90" frameborder="0" align="middle" src="http://download1.csdn.net/down3/20070601/01184120111.htm" marginheight="0" marginwidth="0">
Power up C++ with STL: Part I (introduction, vector)
Power up C++ with STL: Part II (string, set, map)
Power up C++ with STL: Part III (more on STL)
Armed with STL, let's go on to the most interesting part of this tutorial: how to implement real algorithms efficiently.
Depth-first search (DFS)
I will not explain the theory of DFS here – instead, read this section of gladius's Introduction to Graphs and Data Structures tutorial – but I will show you how STL can help.
At first, imagine we have an undirected graph. The simplest way to store a graph in STL is to use the lists of vertices adjacent to each vertex. This leads to the vector< vector<int> > W structure, where W[i] is a list of vertices adjacent to i. Let’s verify our graph is connected via DFS:
That’s all. STL algorithm 'for_each' calls the specified function, 'dfs', for each element in range. In check_graph_connected() function we first make the Visited array (of correct size and filled with zeroes). After DFS we have either visited all vertices, or not – this is easy to determine by searching for at least one zero in V, by means of a single call to find()./*
Reminder from Part 1:
typedef vector<int> vi;
typedef vector<vi> vvi;
*/
int N; // number of vertices
vvi W; // graph
vi V; // V is a visited flag

void dfs( int i) {
if(!V[i]) {
V[i] = true;
for_each(all(W[i]), dfs);
}
}

bool check_graph_connected_dfs() {
int start_vertex = 0;
V = vi(N, false);
dfs(start_vertex);
return (find(all(V), 0) == V.end());
}

Notice on for_each: the last argument of this algorithm can be almost anything that “can be called like a function”. It may be not only global function, but also adapters, standard algorithms, and even member functions. In the last case, you will need mem_fun or mem_fun_ref adapters, but we will not touch on those now.
One note on this code: I don't recommend the use of vector<bool>. Although in this particular case it’s quite safe, you're better off not to use it. Use the predefined ‘vi’ (vector<int>). It’s quite OK to assign true and false to int’s in vi. Of course, it requires 8*sizeof(int)=8*4=32 times more memory, but it works well in most cases and is quite fast on TopCoder.
A word on other container types and their usage
Vector is so popular because it's the simplest array container. In most cases you only require the functionality of an array from vector – but, sometimes, you may need a more advanced container.
It is not good practice to begin investigating the full functionality of some STL container during the heat of a Single Round Match. If you are not familiar with the container you are about to use, you'd be better off using vector or map/set. For example, stack can always be implemented via vector, and it’s much faster to act this way if you don’t remember the syntax of stack container.
STL provides the following containers: list, stack, queue, deque, priority_queue. I’ve found list and deque quite useless in SRMs (except, probably, for very special tasks based on these containers). But queue and priority_queue are worth saying a few words about.
Queue
Queue is a data type that has three operations, all in O(1) amortized: add an element to front (to “head”) remove an element from back (from “tail”) get the first unfetched element (“tail”) In other words, queue is the FIFO buffer.
Breadth-first search (BFS)
Again, if you are not familiar with the BFS algorithm, please refer back to this TopCoder tutorial first. Queue is very convenient to use in BFS, as shown below:
More precisely, queue supports front(), back(), push() (== push_back()), pop (== pop_front()). If you also need push_front() and pop_back(), use deque. Deque provides the listed operations in O(1) amortized./*
Graph is considered to be stored as adjacent vertices list.
Also we considered graph undirected.

vvi is vector< vector<int> >
W[v] is the list of vertices adjacent to v
*/

int N; // number of vertices
vvi W; // lists of adjacent vertices


bool check_graph_connected_bfs() {
int start_vertex = 0;
vi V(N, false);
queue<int> Q;
Q.push(start_vertex);
V[start_vertex] = true;
while(!Q.empty()) {
int i = Q.front();
// get the tail element from queue
Q.pop();
tr(W[i], it) {
if(!V[*it]) {
V[*it] = true;
Q.push(*it);
}
}
}
return (find(all(V), 0) == V.end());
}

There is an interesting application of queue and map when implementing a shortest path search via BFS in a complex graph. Imagine that we have the graph, vertices of which are referenced by some complex object, like:
Consider we know that the path we are looking for is quite short, and the total number of positions is also small. If all edges of this graph have the same length of 1, we could use BFS to find a way in this graph. A section of pseudo-code follows:pair < pair < int , int > , pair < string , vector < pair < int , int > > > >
( this case is quite usual: complex data structure may define the position in
some game, Rubik’s cube situation, etc…)

If the edges have different lengths, however, BFS will not work. We should use Dijkstra instead. It's possible to implement such a Dijkstra via priority_queue -- see below.// Some very hard data structure

typedef pair < pair < int , int > , pair < string , vector < pair < int , int > > > > POS;

// ...

int find_shortest_path_length(POS start, POS finish) {

map<POS, int> D;
// shortest path length to this position
queue<POS> Q;

D[start] = 0; // start from here
Q.push(start);

while(!Q.empty()) {
POS current = Q.front();
// Peek the front element
Q.pop(); // remove it from queue

int current_length = D[current];

if(current == finish) {
return D[current];
// shortest path is found, return its length
}
tr(all possible paths from 'current', it) {
if(!D.count(*it)) {
// same as if(D.find(*it) == D.end), see Part I
// This location was not visited yet
D[*it] = current_length + 1;
}
}
}

// Path was not found
return -1;
}
// ...


Priority_Queue
Priority queue is the binary heap. It's the data structure, that can perform three operations:
- push any element (push)
- view top element (top)
- pop top element (pop)
Dijkstra
In the last part of this tutorial I’ll describe how to efficiently implement Dijktra’s algorithm in sparse graph using STL containers. Please look through this tutorial for information on Dijkstra’s algoritm.
Consider we have a weighted directed graph that is stored as vector< vector< pair<int,int> > > G, where
- G.size() is the number of vertices in our graph
- G[i].size() is the number of vertices directly reachable from vertex with index i
- G[i][j].first is the index of j-th vertex reachable from vertex i
- G[i][j].second is the length of the edge heading from vertex i to vertex G[i][j].first
Dijstra via priority_queuetypedef pair < int , int > ii;
typedef vector < ii > vii;
typedef vector < vii > vvii;

Many thanks to misof for spending the time to explain to me why the complexity of this algorithm is good despite not removing deprecated entries from the queue.
I will not comment on the algorithm itself in this tutorial, but you should notice the priority_queue object definition. Normally, priority_queue<ii> will work, but the top() member function will return the largest element, not the smallest. Yes, one of the easy solutions I often use is just to store not distance but (-distance) in the first element of a pair. But if you want to implement it in the “proper” way, you need to reverse the comparison operation of priority_queue to reverse one. Comparison function is the third template parameter of priority_queue while the second paramerer is the storage type for container. So, you should write priority_queue<ii, vector<ii>, greater<ii> >.
vi D(N, 987654321 );
// distance from start vertex to each vertex

priority_queue < ii,vector < ii > , greater < ii > > Q;
// priority_queue with reverse comparison operator,
// so top() will return the least distance
// initialize the start vertex, suppose it’s zero
D[ 0 ] = 0 ;
Q.push(ii( 0 , 0 ));
// iterate while queue is not empty
while ( ! Q.empty()) {
// fetch the nearest element
ii top = Q.top();
Q.pop();

// v is vertex index, d is the distance
int v = top.second, d = top.first;
// this check is very important
// we analyze each vertex only once
// the other occurrences of it on queue (added earlier)
// will have greater distance
if(d <= D[v]) {
// iterate through all outcoming edges from v
tr(G[v], it) {
int v2 = it->first, cost = it->second;
if(D[v2] > D[v] + cost) {
// update distance if possible
D[v2] = D[v] + cost;
// add the vertex to queue
Q.push(ii(D[v2], v2));
}
}
}
}


Dijkstra via set
Petr gave me this idea when I asked him about efficient Dijkstra implementation in C#. While implementing Dijkstra we use the priority_queue to add elements to the “vertices being analyzed” queue in O(logN) and fetch in O(log N). But there is a container besides priority_queue that can provide us with this functionality -- it’s ‘set’! I’ve experimented a lot and found that the performance of Dijkstra based on priority_queue and set is the same.
So, here’s the code:
One more important thing: STL’s priority_queue does not support the DECREASE_KEY operation. If you will need this operation, ‘set’ may be your best bet.vi D(N, 987654321 );
// start vertex
set < ii > Q;
D[ 0 ] = 0 ;
Q.insert(ii( 0 , 0 ));

while ( ! Q.empty()) {
// again, fetch the closest to start element
// from “queue” organized via set
ii top = *Q.begin();
Q.erase(Q.begin());
int v = top.second, d = top.first;

// here we do not need to check whether the distance
// is perfect, because new vertices will always
// add up in proper way in this implementation
tr(G[v], it) {
int v2 = it->first, cost = it->second;
if(D[v2] > D[v] + cost) {
// this operation can not be done with priority_queue,
// because it does not support DECREASE_KEY
if(D[v2] != 987654321) {
Q.erase(Q.find(ii(D[v2],v2)));
}
D[v2] = D[v] + cost;
Q.insert(ii(D[v2], v2));
}
}
}

I’ve spent a lot of time to understand why the code that removes elements from queue (with set) works as fast as the first one.
These two implementations have the same complexity and work in the same time. Also, I’ve set up practical experiments and the performance is exactly the same (the difference is about ~%0.1 of time).
As for me, I prefer to implement Dijkstra via ‘set’ because with ‘set’ the logic is simpler to understand, and we don’t need to remember about ‘greater<int>’ predicate overriding.
What is not included in STL
If you have made it this far in the tutorial, I hope you have seen that STL is a very powerful tool, especially for TopCoder SRMs. But before you embrace STL wholeheartedly, keep in mind what is NOT included in it.
First, STL does not have BigInteger-s. If a task in an SRM calls for huge calculations, especially multiplication and division, you have three options:
- use a pre-written template
- use Java, if you know it well
- say “Well, it was definitely not my SRM!”
Nearly the same issue arises with the geometry library. STL does not have geometry support, so you have those same three options again.
The last thing – and sometimes a very annoying thing – is that STL does not have a built-in string splitting function. This is especially annoying, given that this function is included in the default template for C++ in the ExampleBuilder plugin! But actually I’ve found that the use of istringstream(s) in trivial cases and sscanf(s.c_str(), …) in complex cases is sufficient.
Those caveats aside, though, I hope you have found this tutorial useful, and I hope you find the STL a useful addition to your use of C++. Best of luck to you in the Arena!
Note from the author: In both parts of this tutorial I recommend the use of some (macro) templates to minimize the time required to implement something. I must say that this suggestion should always be up to the coder. Aside from whether (macro) templates are a good or bad tactic for SRMs, in everyday life they can become annoying for other people who are trying to understand your code. While I did rely on them for some time, ultimately I reached the decision to stop. I encourage you to weigh the pros and cons of templates and to consider this decision for yourself.
width="728" scrolling="no" height="90" frameborder="0" align="middle" src="http://download1.csdn.net/down3/20070601/01184120111.htm" marginheight="0" marginwidth="0">
























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








