c++LCA(最近公共祖先）

• LCA是什么

LCA就是在一棵树上求出两个点的最近公共祖先。

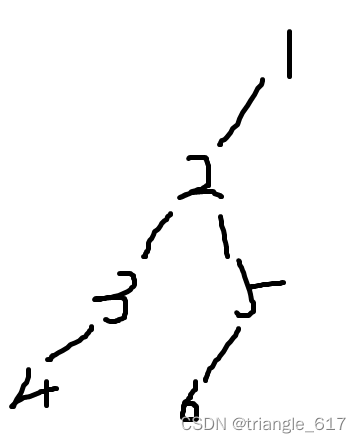
如图，4和6的最近公共祖先为2。

• LCA的求法

先使两个点的深度相等，如果此时两点所表示的数相同，则这个数就是这两个点的最近公共祖先，不然将它们不断上移，并保持它们表示的数不同，最后输出这两个移出的节点的父亲点。

• 代码实现

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5e5 + 110;
int d[N], jump[N][21];//d表示深度，jump[i][j]表示i往上跳2^j步
vector<int> v[N];//树
void dfs(int x, int fa, int sum) {
	jump[x][0] = fa;
	d[x] = sum;
	for (int i = 0; i < v[x].size(); i++)
		if (v[x][i] != fa)
			dfs(v[x][i], x, sum + 1);
}//求父亲点和深度
int lca(int x, int y) {
	if (d[x] < d[y]) swap(x, y);//使x点的深度最大
	for (int i = 20; i >= 0; i--)
		if (d[jump[x][i]] >= d[y])
			x = jump[x][i];//使x,y的深度相等
	if (x == y)
		return x;
	for (int i = 20; i >= 0; i--)
		if (jump[x][i] != jump[y][i])
			x = jump[x][i], y = jump[y][i];
	//将它们不断上移，并保持它们表示的数不同
	return jump[x][0];
}
signed main() {
	int n, m;
	cin >> n >> m;
	for (int i = 1; i < n; i++) {
		int x, y;
		cin >> x >> y;
		v[y].push_back(x);
		v[x].push_back(y);
	}//建树
	dfs(1, 0, 1);
	for (int i = 1; i <= 20; i++)
		for (int j = 1; j <= n; j++)
			jump[j][i] = jump[jump[j][i - 1]][i - 1];
	int a, b;
	cin >> a >> b;
	cout << lca(a, b);
	return 0;
}