豆瓣8.9，这本数学科普书值得出现在国内每一所图书馆里！

转载于 2025-06-03 11:01:23 发布

· 35 阅读

版权

原文链接：https://mp.weixin.qq.com/s?__biz=MjM5Njc0MjIwMA==&mid=2649835660&idx=1&sn=81033ceffdd2fcf8b27712dd8d63de29&chksm=bf3a78d90e8b62cbd7459b26420579645341240990d36f14fe1da3f39d1df8b15cf8a72461e1&scene=126&sessionid=0

去年7月的时候，图灵上市了《数学的雨伞下：理解世界的乐趣》，这本书是法国巴黎高等师范学院概率学博士米卡埃尔·洛奈的著作，全书没有用一个公式，却讲清楚了数学思维到底是什么。

一上市，就受到了科普圈的热烈追捧，更是获得了第十九届文津图书奖科普类提名图书、2023年度《环球科学》·最美科学阅读榜单、清华大学阅读推荐等，被读者称为“读过的最丝滑数学科普书，没有之一”。

同时这本书也受到了读者的广泛喜爱，豆瓣上9的高分，微信读书上也是好评如潮。毫不夸张的说，这本是值得出现在国内每一所图书馆里！

如果你不愿意读复杂繁琐的数学公式，却又希望领略数学之美的乐趣，那么这本书就是最好的选择。

《数学的雨伞下：理解世界的乐趣》

作者：[法] 米卡埃尔•洛奈（Mickaël Launay）

译者：欧瑜

对数之桥

位于苏格兰爱丁堡中心地段的墨奇斯顿住宅区通常比较安静。这里宁静的街道旁矗立着一眼望不到头的大型住宅和整齐排列的小花园，在距离首都中心仅几分钟路程的地方笼罩着一派宁静而单调的氛围。幼发拉底河热闹喧腾的河岸和苏格兰气氛之间的文化差异直闯眼帘。

回首过去，我总会生出某种感怀，我瞥见了科学历史和数学历史的恢宏接力，而每一个民族，无论在它与其他民族之间可能横亘着什么，都为这接力做了一份贡献。是的，故事就在这里继续。就是在这里，美索不达米亚的书吏找到了他们的继承者。

我们的下一个约定地点就在几条街之外。

向南朝莫宁赛德前行，我们来到龙比亚大学（Napier University），每年都有 25 000 多名学生在这里学习计算机、戏剧或犯罪学。当你在校园里四处走动的时候，用 20 世纪的混凝土建造的、只点缀着几块现代感十足的玻璃幕墙的校园建筑会让你感到有些沮丧。

但是，如果你大起胆子走到建筑物的里面，你就会发现这所大学的瑰宝。在树有围栏的建筑物中央，耸立着好像深嵌其中、几乎被新近建筑物吞噬的墨奇斯顿塔楼。

这是一幢方形建筑，古老的石块上布满岁月的痕迹，几扇窄而深的窗户不规则地镶嵌在上面。锯齿形的屋顶犹如一顶王冠，让塔楼在不知曾多少次濒临坍塌的墙壁的掩映下，露出一副自豪而高贵的身姿。以前，这座塔楼曾是一座小城堡的一部分。

1550 年，约翰·纳皮尔（John Napier）就出生在墨奇斯顿城堡（图 1.16），他的名字被冠在一所大学和一种彻底改变了科学的数学运算之上。约翰·纳皮尔是一个奇异的人物。

就像那个时代的许多学者一样，他涉猎各类学科，从神学到天文学，还有数学。关于他，坊间流传着一件逸事，尽管跟数学没有什么关系，却可以让我们从中窥见几分他的性格。

纳皮尔有个叫罗斯林（Roslin）的邻居，邻居养的鸽子每天飞到纳皮尔的院子里吃谷粒。纳皮尔很生气，警告邻居说，如果管不住这些鸟，他就要直接把它们没收了。那个叫罗斯林的人对他嗤之以鼻，说他尽管可以去追捕那些鸽子。

第二天早上，邻居惊讶地看到这位数学家手里拿着个大袋子，正轻而易举地捉着他所有的鸽子，而那些鸽子甚至都没有挣扎着逃走。头天晚上，纳皮尔在自家院子里撒满了浸泡过白兰地的谷粒。到了早晨，吃了谷粒的鸽子全都酩酊大醉，无法飞翔，一只只束手就擒。

图 1.16　约翰·纳皮尔，墨奇斯顿城堡

这个故事很可能只是传闻，但它告诉我们一件事：纳皮尔擅长用意想不到的办法去解决问题。有时候，你只需要改变视角就能找到解决办法。如果找到了正确的视角，最棘手的情况也会变得易如反掌。如果你不如鸽子灵巧，那就让鸽子变得不如你灵巧。解决重大问题并不总是得更聪明、更强大或更迅速。最重要的是找到窍门。

纳皮尔后来把这种出其不意的思维方式用在了数学上：他发明了一种革命性的绝妙运算。这种运算将令几代科学人的生活更加便利，直至 20 世纪末。这种运算能够将乘法变成加法。

为此，他想到把一根乘法轴和一根加法轴平行放置。在乘法轴上，每个分度对应前一个分度乘以 2；在加法轴上，每个分度对应前一个分度加 1（图 1.17）。

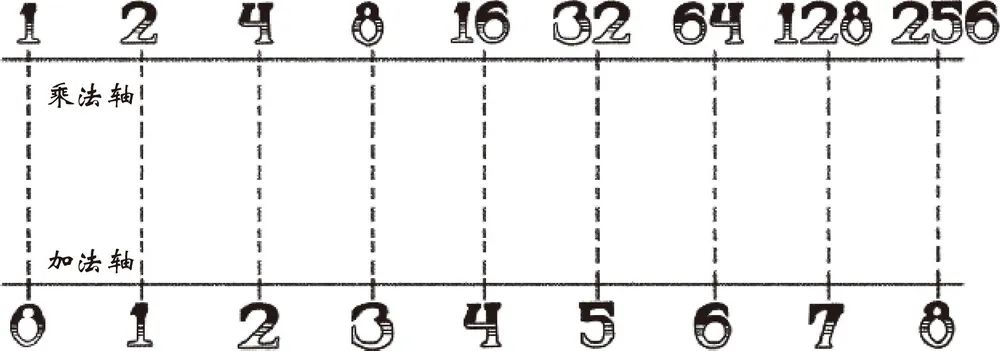
图　1.17

通过这种平行对照，这位苏格兰数学家在加法世界和乘法世界之间架起了一座桥梁。借助这一简单的图表，从加法穿梭到乘法的旅行在一瞬间成为可能，两者之间的界限突然消失了。顶部的 8 对应底部的 3，底部的 5 对应顶部的 32，依此类推。而顶部的乘法则对应底部的加法。

为了让你能够清楚地理解这一原理，我们来举个例子。假设你想进行 8×16 的乘法运算，那么算法就是下面这个样子。

把这个算法带入加法的世界：8×16 变成了 3+4；
计算：3+4=7；
把你的结果重新带回乘法的世界：7 变成了 128。

你得到的结果是：8×16=128。从图上来看，推理过程遵循的是以下路径（图 1.18）。

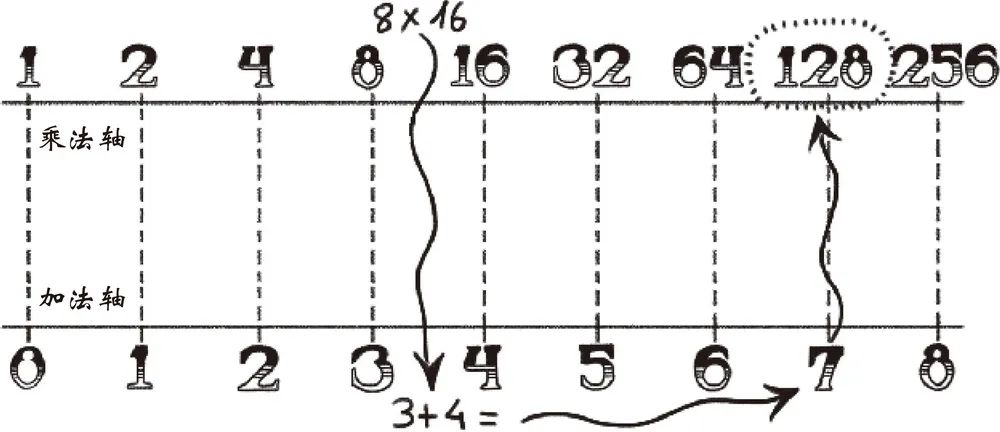
图　1.18

这看起来就像是魔术！这种简单的匹配似乎完美得不像是真的，但效果却很好。8 和 16 没有什么特别之处，你可以用其他数试一试，约翰·纳皮尔的方法适用于所有的乘法计算。

那么当然了，这个例子是最基本的示例，因为 8 和 16 是很简单的数。但假设你要对复杂得多的数进行乘法运算，比如 2.43 乘 78.35。再假设你的书桌上放着一本加法 / 乘法对照表，这本对照表远比我们在上文中画的那两根轴要完整得多。

通过在表中查找数，你把乘法2.43×78.35 变成了加法 1.281+6.292。你在几秒之内算出了和：7.573。然后，你把这个结果带回到乘法中，积约为：190.4。你刚刚在不到 30 秒里完成了乘法运算。如果没有这本目录，你很可能需要一分多钟才能得出乘法的结果。

纳皮尔花了二十多年才发展出这一理论并制定出加法 / 乘法表。他当然是在没有计算器的情况下进行的。所有的计算都是他手工完成的。他在 1614 年发表了一部名为《奇妙的对数表的描述》（Mirifici logarithmorum canonis descriptio）的作品，并借机发明了“对数”4 这个词，用来指称乘法世界和加法世界之间的那座桥梁。

更确切地说，对数是从乘法轴到加法轴的通道：8 的对数是 3，16 的对数是 4，依此类推。

4这个词是由意为“关系”的希腊语词根“λόγος”（lógos）和意为“数字”的希腊语词根“ἀριθμός”（arithmos）构成的。

纳皮尔在书的前半部分介绍了这一理论，详细说明了对数的定义及其数学特性，而后半部分则完全由所占篇幅达近百页的数字表构成。这些数字表是对数表，也就是你计算所需的加法 / 乘法对照表。

纳皮尔在第一个版本中罗列了 5400 个数。你在寻找某个对数吗？你只需翻看这些纸页就能在几秒内找到它。

老实说，我们必须承认，使用纳皮尔对数表获得的结果只是近似值，因为它给出的对数只精确到小数点后三或四位。如果你想获得误差范围更小的结果，这就会是个问题。但对于当时大部分天文学或建筑学中的计算来说，这个精确度已经绰绰有余。

但是，至于这个对数表能否良好运转，可能会有人提出异议，因为数存在无限性。不过，无论纳皮尔的对数表有多么可观，它都无法囊括数量无限的对数——对数表被限制在一定数量的纸页内，并在某处打住。因此，这种方法似乎不可能涵盖所有可能的和可以想见的乘法。

其实，这是有可能的。就在此时，美索不达米亚书吏们那引人入胜的不变量冲破时间的暗夜，回到了舞台上。想要完成所有的乘法运算，你并不需要所有数的对数。比如，你只需要知道 1 到 1000 的所有对数就足够了，然后抛却零和小数点进行计算。

假设你需要对 1.28 和 2500 做乘法。把零和小数点去掉，这两个数就可以进入你的对数表所覆盖的范围之内，变成 128 和 25。现在，你可以使用对数表来查找乘法的运算结果：32（依然没有零和小数点）。然后，你只需要判断结果的数量级，就可以把小数点和零放在正确的位置上了。1.28×2500=3200。只要稍加练习，这种技术就能让你在片刻之间完成所有的乘法。

在计算机和电子计算器的时代，似乎很难想象对数在纳皮尔那个时代产生的影响。对我们而言，加法和乘法之间的这座桥梁可能很稀罕，它是一种看待事物的方式，非常有趣，甚至很有启发性，但没有太大的意义。

然而，在问世之后的几年中，这些对数表以极快的速度在整个科学界传播开来，并成为各个领域学者的主要工具之一。这些对数表还被科学界以外需要进行流水线式计算的众多行业的从业者所使用，比如建筑师、会计师和行政人员。直到 20 世纪下半叶，大多数小学生仍须把这些对数表带在书包里。

继纳皮尔之后，又有几位数学家着手计算并发布了更为精确和更为完整的对数表。卡米耶·布瓦尔（Camille Bouvart）和阿尔弗雷德·拉蒂尼（Alfred Ratinet）在 19 世纪末制定的新对数表有过 70 多个版本，并在不到一个世纪内成为数学史上最畅销的读物之一。

想要知道为什么这些新对数表会如此成功，我们就必须认识到当时的科学家需要处理的海量计算。我所说的并不是需要长时间思考、需要一定程度创新和研究的智力型计算。不是那样的，我说的是蠢笨而惹人厌烦的计算。这些计算毫无挑战可言，你从一开始就知道怎么去做，但仍然需要耗费海量的时间。

所有的数学家都知道如何计算 2.35847×78.3564。没有任何悬念，但算式很长。如果你研究的是天文学，那你可能需要把数十种乃至数百种同类型的乘法运算串联起来，才能获得想要的结果。

今天，负责进行这些计算的是计算机。在纳皮尔的时代，一切都必须手动完成！计算得用纸和笔，有时会借助算盘。你可以想见对数表的出现可以让这些人节省多少时间。对数表使耗费一整天的烦琐计算减少到只需两或三小时成为可能！

18 世纪末，当时最伟大的数学家之一——皮埃尔 - 西蒙·拉普拉斯（Pierre-Simon Laplace）断言，对数让天文学家免于和冗长计算密不可分的错误和厌倦，从而在某种程度上使得他们的生命延长了一倍。

到了 20 世纪末，电子机器问世，对数最终失去了其首要的用途。而在今天，再也没有人会使用纳皮尔的对数表去进行冗长的计算了。但是，对数犹如一只在数学领域浴火重生的凤凰，找到了其他的应用领域。在那以后，问题不再是技术，而是理解。

如我们所见，这个环绕着我们的宇宙主要是以乘法的方式构建而成的，而科学仍然常常需要从乘法的世界转入加法的世界。每一次需要这么做时，科学就会重新启用这座由纳皮尔在四百多年前搭建的古老的对数之桥，而这座桥梁被使用的频率丝毫不逊从前。

因此，按照对数标度来对事物进行排列往往是有益之举。衡量地震强度的里氏震级就是一个很好的例子。在里氏震级中，标度每增加一度，代表现实中的振幅增加 10 倍。照此，7 级地震的振幅就比 6 级地震的振幅要大 10 倍。

人类有史以来记录到的最强烈的地震是 1960 年 5 月 22 日发生在智利瓦尔迪维亚的地震。这一地震震级为 9.5 级，其振幅要比人类几乎感觉不到的 3.5 级普通地震大一百万倍（图 1.19）。

图　1.19

因此，使用对数标度可以让我们从整体上更好地了解所测地震的振幅差异。如果把这些地震振幅放到一根加法轴上，我们会发现，1 到 7 级的振幅全都缩到了一个点上，读数也变得费力很多（图 1.20）。

图　1.20

在众多以对数标度来测量的物理现象中，我们会看到各种不同的例子，比如以分贝为单位的声音强度、以 pH 为单位的溶液酸度，或是天空中恒星的星等。

另一种常见的情况就是音阶。音符的特征是其在空气中传播的振动频率。因此，你可以在钢琴琴键上演奏不同音高的 la，它们依次具有每秒振动 55、110、220、440、880、1760 和 3520 次的频率。

你会发现，每两个音符之间相隔一个八度音程，音高较高的音符，其振动频率是音高较低者的两倍。当你观察吉他琴颈上的品位时，音符的这种乘法就会尤为明显。这些品位不是按照固定音差排列的，而是按照乘法递增排列的，离琴头越近，音差就越大（图 1.21）。

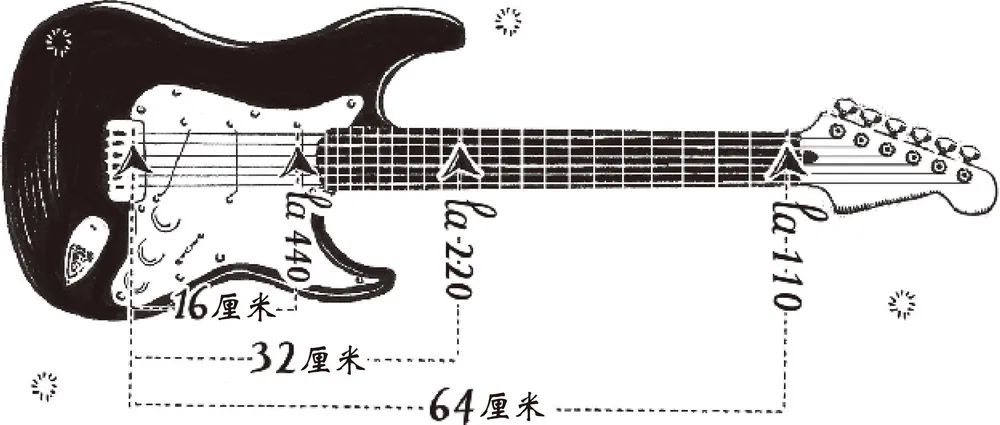
图　1.21

如果你在同一根弦上弹奏相差一个八度音程的两个不同音符，那么弹奏出最低音的品位与琴桥的距离，就是弹奏出最高音的品位与琴桥的距离的两倍。照此，在第五根弦上，“振动频率为 110Hz 的 la”就会在距离琴桥 64 厘米的位置上，而“振动频率为 220Hz 的 la”就会在距离琴桥 32 厘米的位置上，即 64 厘米的一半。

而要在同一根弦上奏出“振动频率为 440Hz 的 la”，就要把手指按在距离琴桥 16 厘米处的品位上，“振动频率为 880Hz 的 la”则在距离琴桥 8 厘米的品位上。不管怎样，从理论上来讲，由于这些动作做起来很复杂，因此在实际操作中，我们会在同一根弦上弹奏这两个 la。

尽管约翰·纳皮尔的思维方式极尽创意，但在发表研究成果时，他本人很可能从未料到自己那些奇妙的对数会对这个世界产生如此广泛的影响。

对于这些不同的例子，需要补充的一点是，随着对数的出现，我们就拥有了需要用来理解本福特定律的所有数学拼图块了。剩下的就是等待一个天才的头脑来把它们拼接起来。而我们调查的终章将在美国上演。

推荐阅读