非负矩阵分解中基于L1和L2范式的稀疏性约束

L1、L2范式

    假设需要求解的目标函数为：

                    E(x) = f(x) + r(x)

    其中f(x)为损失函数，用来评价模型训练损失，必须是任意的可微凸函数，r(x)为规范化约束因子，用来对模型进行限制，根据模型参数的概率分布不同，r(x)一般有:L1范式约束(模型服从高斯分布)，L2范式约束(模型服从拉普拉斯分布)；其它的约束一般为两者组合形式。

    L1范式约束一般为：

        

    L2范式约束一般为:

            

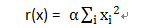
     L1范式可以产生比较稀疏的解，具备一定的特征选择的能力，在对高维特征空间进行求解的时候比较有用；L2范式主要是为了防止过拟合。

稀疏性约束

    在文章Non-negative Matrix Factorization With Sparseness Constraints中，将L1范式和L2范式组合起来形成新的约束条件，用稀疏度来表示L1范式和L2范式之间的关系：

                    

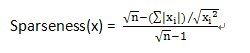
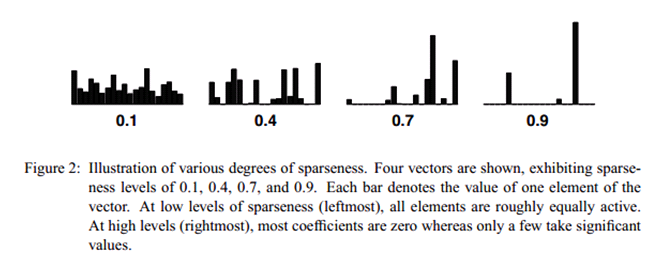
    当向量x中只有一个非零的值时，稀疏度为1，当所有元素非零且相等的时候稀疏度为0。n表示向量x的维度。不同稀疏度的向量表示如下：

                   

    NMF with Sparseness Constraint

    目标函数：

                   

    算法流程如下：

                                    

    算法中一个很重要的步骤是投影算法，即给定向量x和L2、L1值，找到给定稀疏度的投影向量。投影算法如下：

                           

      算法至多迭代dim(x)次就会收敛，因为每次迭代的时候至少会产生一个新的非零值，所以速度还是很快的。算法的matlab代码在 http://www.cs.helsinki.fi/patrik.hoyer/上，投影部分的python代码如下：

[python]  view plain copy

1. #!/usr/bin/python  
2. #-*-coding:utf-8-*-  
3.   
4. from __future__ import division  
5. import math  
6. import sys  
7. #import numpy  
8.   
9.   
10.   
11. """desiredsparseness can be set [0.1,0.2,0.3,0.4,0.5]"""  
12. def l1sparse(dimension,desiredsparseness):  
13.     return math.sqrt(dimension) - (math.sqrt(dimension)-1)*desiredsparseness  
14.   
15.   
16. def vsum(vector):  
17.     sum = 0  
18.     for v in vector:  
19.     sum += v  
20.     return sum  
21. def v2sum(vector):  
22.     sum = 0  
23.     for v in vector:  
24.     sum += v*v  
25.     return sum  
26.   
27. def vadd(vector,factor):  
28.     vresult = []  
29.     for v in vector:  
30.     v += factor  
31.     vresult.append(v)  
32.     return vresult  
33.   
34. def vmultip(vector,factor):  
35.     vresult = []  
36.     for v in vector:  
37.     v = v*factor  
38.     vresult.append(v)  
39.     return v  
40.   
41. def ones(dimension,num):  
42.     v = []  
43.     for i in xrange(dimension):  
44.     v.append(num)  
45.     return v  
46.   
47. def vdec(svector,dvector):  
48.     vresult = []  
49.     for i in xrange(len(svector)):  
50.     t = svector[i]-dvector[i]  
51.     vresult.append(t)  
52.     return vresult  
53.   
54. def vaddv(svector,dvector):  
55.     vresult = []  
56.     for i in xrange(len(svector)):  
57.     t = svector[i] + dvector[i]  
58.     vresult.append(t)  
59.     return vresult  
60. """This should inverse svector first 
61.    svector:N*1 
62.    dvector 1*N"""  
63.   
64. def vmultipv(svector,dvector):  
65.     sum = 0  
66.     for i in xrange(svector):  
67.     sum += svector[i]*dvector[i]  
68.     return sum  
69.   
70. def checknon(svector):  
71.     valid = True  
72.     for v in svector:  
73.     if v<0:  
74.         valid = False  
75.         break  
76.     return valid  
77.   
78. def findne(svector):  
79.     vresult = []  
80.     for i in xrange(len(svector)):  
81.     if svector[i]<0:  
82.         vresult.append(i)  
83.     return vresult  
84.   
85. """ This function solves following : 
86.     Given a vector svector,find a vector k which  
87.     having sum(abs(k))=l1norm;sum(k,2)=l2norm ; 
88.     and is closest to svector in euclidian distance 
89.     if nn is set to 1 ,and the elements of k is 
90.     restricted to non-nagative"""  
91.   
92. def projfuc(svector,l1norm,l2norm,nn):  
93.     N = len(svector)  
94.     sum = vsum(svector)  
95.     factor = (l1norm-sum)/N  
96.     v = vadd(svector,factor)  
97.     zerov = []  
98.     j = 0#iter times  
99.     while 1:  
100.         p = ones(N,1)  
101.     factor = l1norm/(N-len(zerov))  
102.     midpoint = vmultip(p,factor)  
103.     for vp in zerov:  
104.         midpoint[vp] = 0  
105.     w = vdec(v,midpoint)  
106.     a = v2sum(w)  
107.     b = vmultipv(w,v)*2  
108.     c = v2sum(v)-l2norm  
109.     alphap = (-b+float(math.sqrt(b*b-4*a*c)))/(2*a)  
110.     v1 = vmultip(w,alphap)  
111.     vnew = vaddv(v1,v)  
112.     valid = checknon(vnew)  
113.     if valid:  
114.         j +=1  
115.         v = vnew  
116.         break;  
117.     j+=1  
118.     zerov = findne(vnew)  
119.         for vp in zerov:  
120.         vnew[vp] = 0  
121.     sum = vsum(vnew)  
122.         factor = (l1norm-sum)/(N-len(zerov))  
123.         v = vadd(vnew,factor)  
124.         for vp in zerov:  
125.         v[vp] = 0  
126.       
127.     return