一.映射与函数

一.映射

映射: 用于反应非空集合之间数据的对应关系。
定义: 存在两个A、B为非空集合,A中的任意元素即任意x∈A,都有唯一确定的y∈B与之对应。对应关系为y=f(x)

1.单射

单射: y=f(x)的映射集合A,B中,x1,x2∈A，x1≠x2，都有f(x1)≠f(x2)。即集合A中没有两个元素在映射后产生相同的输出值

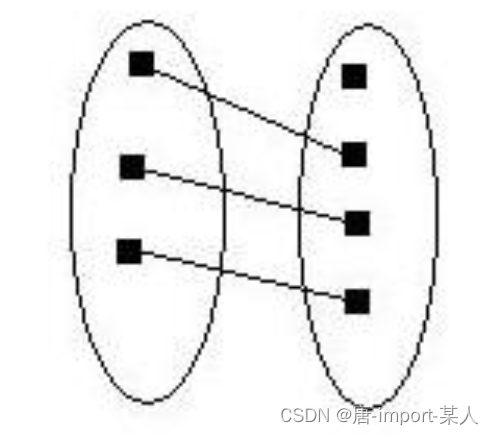
2.满射

满射: y=f(x)的映射集合A,B中,x∈A，f(x)都能在集合B中找到落点。即集合A中映射的输出值覆盖了整个集合B。

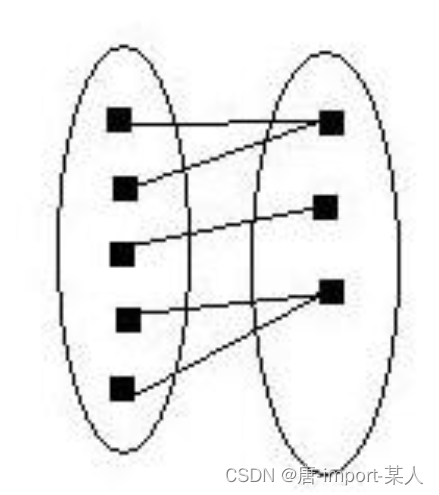
3.双射

双射: y=f(x)的映射集合中,即满足单射,有满足双射。

4.平行传递

平行传递: X与集合Y双射,Y与Z双射。可推导X与Z双射

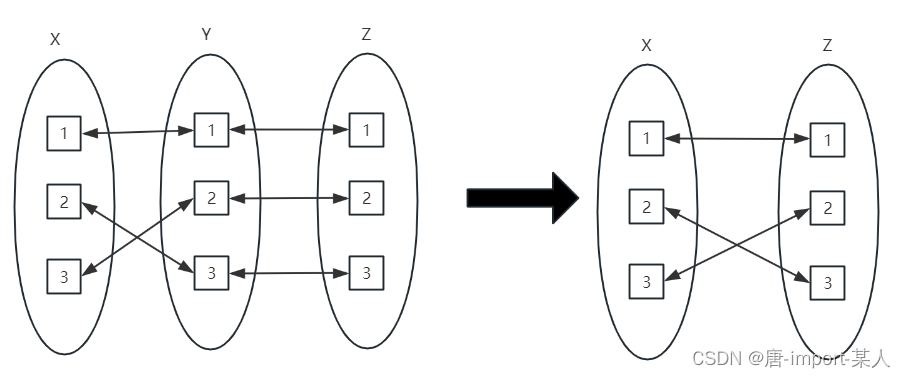
二函数

1.领域

设δ>0. 实数集 U δ ( X 0 ) = { X ∣ ∣ X − X 0 ∣ < = δ } U_δ(X_0)=\{X||X-X_0|<=δ\} Uδ​(X0​)={X∣∣X−X0​∣<=δ}称为$X_0$的δ某领域

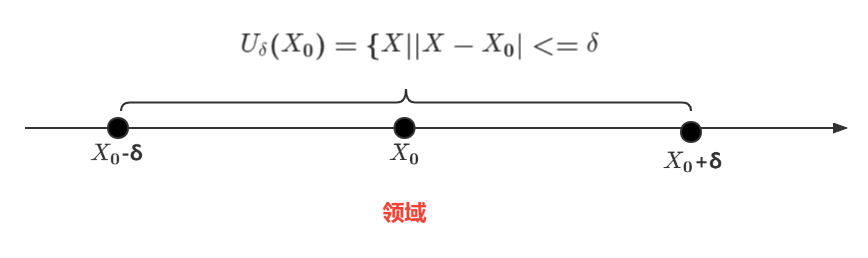
1.1.去心领域

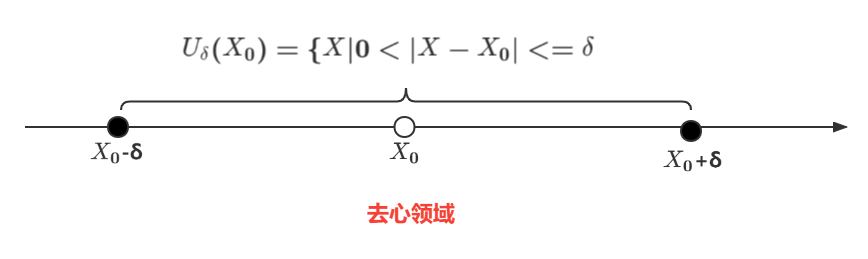
1.2.左领域

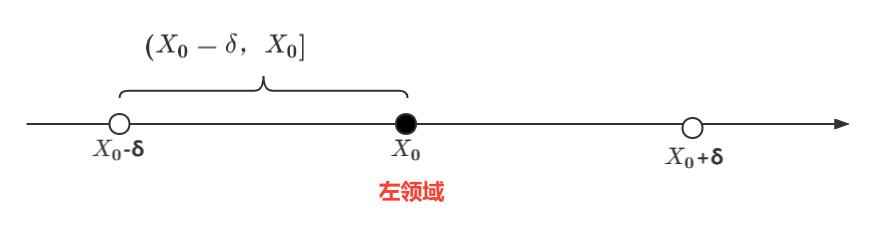
1.3.左空心领域

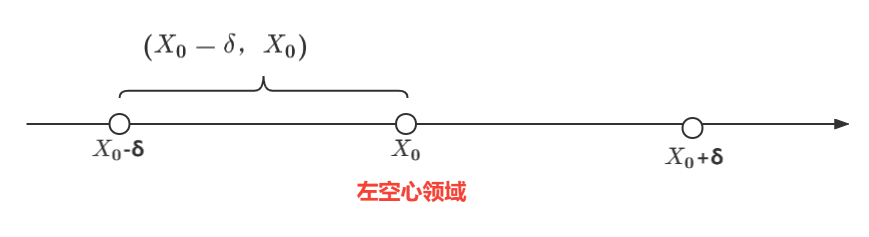
1.4右领域

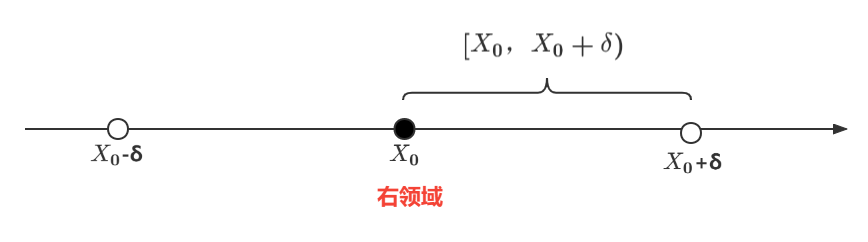
1.5右空心领域

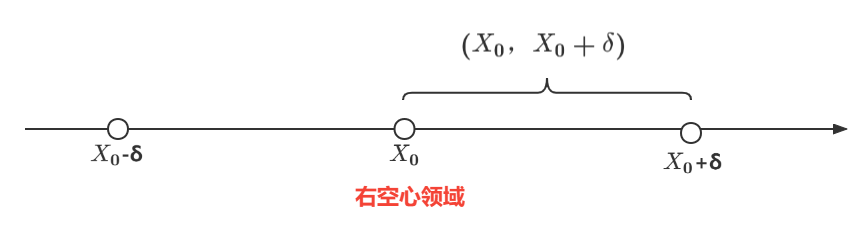
2.函数

设有两个变量x,y。X是非空实数集,每一个x属于X,记为x∈X,存在规则f,x与y有唯一确定的对应的实数。x是自变量,X是定义域,y是因变量,Y是值域,f表示映射规则
Y = { y ∣ y = f ( x ) , x ∈ X } Y=\{y|y=f(x),x∈X\} Y={y∣y=f(x),x∈X}

2.1.绝对值函数

$$y=|x|=\{\begin{array}{l}x,x>0\\ 0,x=0\\ -x,x<0\end{array}$$

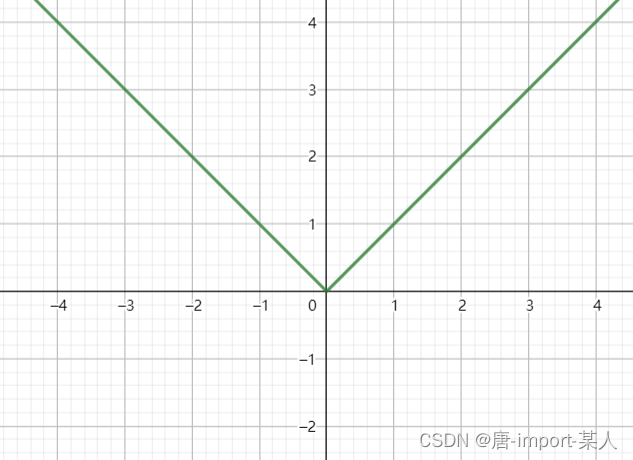
2.2.符号函数

$$y=sgnx=\{\begin{array}{l}1,x>0\\ 0,x=0\\ -1,x<0\end{array}$$

2.3.取整函数

$$
y=[X]

$$

2.4.狄里克函数

$$D(x)=\{\begin{array}{l}1,x为有理数\\ 0,x为无理数\end{array}$$

2.5.隐函数

明确存在一个函数关系F,这个F无法求出精确的解,可以确$y=F(x),x\in X,y\in Y中$

2.6.参数示表示的函数(映射的平行传递)

$x=x(t),y=y(t),x\in X,y\in Y,t\in T$,若在实数集X内每取一个值时,X与T,Y与T双射映射。则确定了Y与X有映射关系,可构成函数$y=f(x)$

三函数特有特性

1.函数的单调性

前提: $f(x)$在实数集$X$上有定义,对任意$x_1,x_2\in X,x_1<x_2$一定存在

• 单调递增(递减)
  $$f(x_1)\le f(x_2),f(x_1)\ge f(x_2)$$
• 严格单调递增(递减)
  $$f(x_1)<f(x_2),f(x_1)>f(x_2)$$

2.函数奇偶性

前提: $f(x)$在实数集$X$上有定义,$x\in X$

• 偶函数(y对称)
  $$f(-x)=f(x)$$
• 奇函数(原点对称)
  $$f(-x)=-f(x)$$

3.函数周期性

前提: $f(x)$在实数集$X$上有定义,$x\in X$,存在常数$T>0,x\pm T\in X$
$$f(x+T)=f(x)$$
周期为：$T$

4.函数有界性

前提: $f(x)$在实数集$X$上有定义,$x\in X$,存在常数$M,m$

• 有上界M
  $$f(x)\le M$$
• 有下界m
  $$f(x)\ge m$$
• 无上界
  $$f(x)\le +\infty$$
• 无下界
  $$f(x)\ge -\infty$$

5.反函数

前提: $y=f(x),x\in X,y\in Y$中集合X与Y的关系是双射
存在Y到X的映射关系$x=g(y)$,表示集合Y到X的映射,则$y=f(x)$存在反函数$y=f^{-1}(x)$即$x=g(y)$

• 推到关系： $y=f(f^{-1}(y))$,$x=f(f^{-1}(x))$
• 价值: 在复杂函数求解中,可以凑出反函数来逃脱寻找具体函数

6.复合函数

前提: 有函数$y=f(x),x\in F_X,y\in F_Y$和$g=G(x),x\in G_X,g\in G_Y$,若$R_g$。若$F_X\cap G_X\ne \varnothing$
$y=f(g(x))$为复合函数,定义域$F_X\cap G_X$,$g(x)$为中间变量,$x$为自变量

四.奇偶公式

$$奇函数\ast 奇函数=偶函数$$
$$偶函数\ast 偶函数=偶函数$$
$$奇函数\ast 偶函数=奇函数$$
$$奇函数复合奇函数=奇函数$$
$$偶函数复合偶函数=偶函数$$
$$偶函数复合奇函数=偶函数$$
$$有对称原点的函数必可分解成一奇一偶$$

五.函数有界充要条件

1.$x->x_0^{-}$有界

• $若存在\underset{n->x_0^{-}}{\lim }f(x)有界$,当x从小于$x_0$的数趋近于$x_0$时f(x)趋近一个常数
• 数学表达:$\exists M(\forall \sigma (\sigma <0\wedge \sigma <x-x_0<0)\Rightarrow f(\sigma )<M)$
  • 存在数M,存在一个从小于$x_0$方向趋近于$x_0$的变量$\sigma$使得$f(\sigma )<M$

2.$x->x_0^{+}$有界

• $若存在\underset{n->x_0^{+}}{\lim }f(x)有界$,当x从大于$x_0$的数趋近于$x_0$时f(x)趋近一个常数
• 数学表达:$\exists M(\forall \sigma (\sigma >0\wedge 0<x-x_0<\sigma )\Rightarrow f(\sigma )<M)$
• 存在数M,存在一个从大于$x_0$方向趋近于$x_0$的变量$\sigma$使得$f(\sigma )<M$

3.$x->x_0$有界

• $若存在\underset{n->x_0}{\lim }f(x)有界$,当x从任意方向趋近于$x_0$时f(x)趋近一个常数
• 数学表达:$\exists M(\forall \sigma (\sigma >0\wedge 0<|x-x_0|<\sigma )\Rightarrow f(x)<M)$
• 存在数M,存在一个任意方向趋近于$x_0$的变量$\sigma$使得$f(\sigma )<M$

4.$x->\infty$有界

• $若存在\underset{n->\infty }{\lim }f(x)有界$,当x趋近于$\infty$时f(x)趋近一个常数
• 数学表达:$\forall X(X>0\wedge |x|>X)\Rightarrow f(x)<M$
• 任意存在大于0的数X,无论x取多少总有值大于或小于它的X存在,使得满足$f(x)<M$

5.最值有界

$f(x)$值域上有最值,则$f(x)$有界