hdu 4556

最新推荐文章于 2024-11-15 17:31:15 发布

u010074900

最新推荐文章于 2024-11-15 17:31:15 发布

阅读量210

点赞数

分类专栏：数论文章标签： c/c++ 数据结构与算法

本文链接：https://blog.csdn.net/u010074900/article/details/84434095

版权

数论专栏收录该内容

3 篇文章 0 订阅

订阅专栏

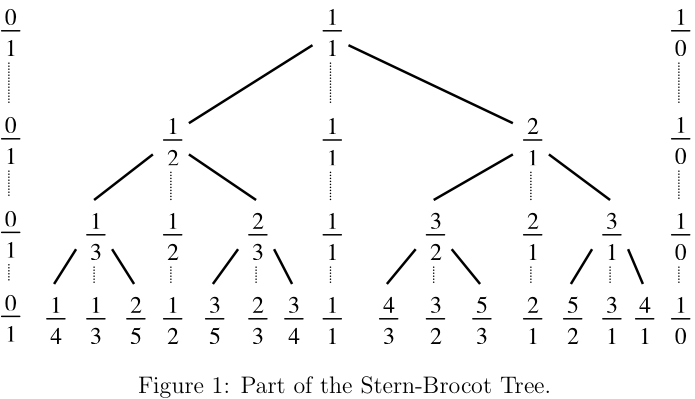
题目大意：求出第n行的符号要求的元素总数。

首先需要明确两个概念：

1.法里数列：n阶法里数列表示从0到1之间分母不大于n的最简分数集合。

同时对于法里数列的长度我们有如下计算公式

$|F_n| = |F_{n-1}| + \varphi(n)$ 。

其中φ(n)表示欧拉函数。

2.欧拉函数：

欧拉函数表示小于或等于n的正整数中于n互质的数的个数，例如φ(8)= 4 ={1,3,5,7}；

求欧拉函数的模板如下：

long long eular(int n)
{
    Eular[1]=1;
    for(int i=2;i<=n;i++)
    if(!Eular[i])
        for(int j=i;j<=n;j+=i)
        {
            if(!Eular[j])
                Eular[j]=j;
            Eular[j]=Eular[j]/i*(i-1);
        }
}

本题的Stern-Brocot Tree 实际上就是一个对称的数据结构，他的左半边是法里数列的结构，因此用对称的观点就能解决了。

#include <cstdio>
#include <iostream>
#define My_Max 1000011
using namespace std;

long long Eular[My_Max];
long long res[My_Max];

long long eular(int n)
{
    Eular[1]=1;
    for(int i=2;i<=n;i++)
    if(!Eular[i])
        for(int j=i;j<=n;j+=i)
        {
            if(!Eular[j])
                Eular[j]=j;
            Eular[j]=Eular[j]/i*(i-1);
        }
}

void Pre()
{
    eular(My_Max-1);
    res[1]=2;
    res[2]=3;
    for(int i=3;i<My_Max;i++)
        res[i]=res[i-1]+Eular[i];
}

int main()
{
    int n;
    Pre();
    while(scanf("%d",&n)!=EOF)
    {
        long long s=(res[n]-2)*2+3;
        cout<<s<<endl;
    }

    return 0;
}

这题错了2次，原因还在于一个概念的问题。

64位整数可以使用int64和longlong两种表示，但是有的oj只识别longlong表示方法，输出上I64d和lld都行，但是有的编译器如codeblocks和mingw只支持I64d输出。比赛前应该弄懂这些信息，当然如果使用cin，cout就没问题了，但是速度相对C语言会慢一点。