汉诺塔问题——从分析到编码

——日记伴我成长

原始问题：有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆：

　　1. 每次只能移动一个圆盘；

2. 大盘不能叠在小盘上面。

大家看图：

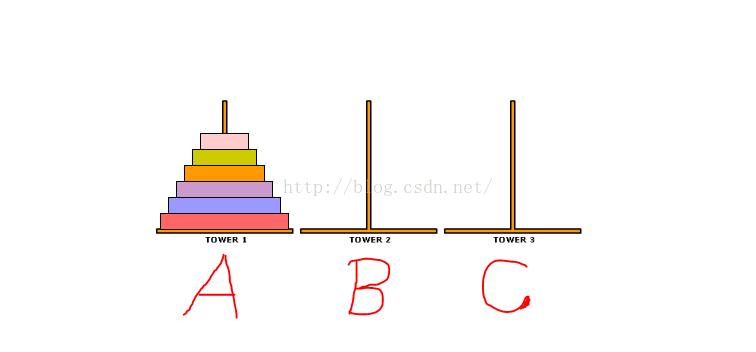
提示：可将圆盘临时置于B杆，也可将从A杆移出的圆盘重新移回A杆，但都必须遵循上述两条规则。

 

汉诺塔的题意比较容易理解，我们首先来分析下当A塔上有1,2,3个圆盘时，盘子的移动情况：

1.  当A塔中只有1个圆盘时，可将一个圆盘直接从A移动到C，移动步为1；

2.  当A塔中有2个圆盘时，可先将第一个移动到B，然后将第二个移动到C，然后再将B上的盘移动到时，移动完成。移动步数为3；

3.  当A塔中有3个圆盘时，这时情况将变得比较复杂。为了简化模型，可将A上的第一个圆盘和第二个圆盘考虑成一个圆盘，这时移动过程和A塔中有2个圆时是一样的。事实上，当A塔中圆盘数为3时，具体的移动步骤如下图所示，移动步数为7。

分析：当A塔中有3个圆盘时，为了将最大的圆盘移动到C塔里，需要借用B塔，此时，三个盘A、B、C分别为原塔，借用塔和目标塔。在将最大的圆盘移动到C 塔后，此时三个塔的状态为：A塔中无盘，B塔中有两个，从上到小为一小一大圆盘，C塔上为原A塔上最大的盘。为了将B塔中的两个圆盘移动到C塔上，需要借用A塔，此时三个盘A、B、C分别为借用盘，原盘和目标塔。当A借中原始盘数足够大时，A塔与B塔总在借用塔与原塔之间进行角色转换，即为了将A塔上n个圆盘移动到目标塔上，需要将n-1个圆盘先移动到借用盘上。

 

编码

汉诺塔的经典解法是利用递归的思想，即，为了将A塔（源塔）上n个圆盘移动到目标塔上，需要将n-1个圆盘先移动到借用塔上，然后再将A塔（源塔）上的第n个圆盘（也就是最大那个）移动到目标塔上。这样，编码就相对简单了。代码如下：

#include <stdio.h>
#include<stdlib.h>
#define _CRT_SECURE_NO_WARNINGS
int i = 1;//记录步数  
void move(int n, char from, char to) //将编号为n的盘子由from移动到to  
{
	printf_s("第%d步:将%d号盘子%c---->%c\n", i++, n, from, to);
}

//第2,3,4个参数代表的意义为源塔，借用塔和目标塔 
void hanoi(int n, char A, char B, char C)//这里的A、B、C分别为源塔，借用塔和目标塔 
{
	if (n == 1)
		move(1, A, C);//只有一个盘子是直接将源塔上的盘子移动到目的塔 
	else
	{
		hanoi(n - 1, A, C, B);//先将源塔（这时为A）的前n-1个盘子借助借用塔（此时为C）移动到目标塔（此时为C）上  
		move(n, A, C);              //将源（这时为A）塔上的最后一个圆盘移动到目标（此时为C）塔上，可以见到，C塔总是作为目标塔。
		hanoi(n - 1, B, A, C);//最后将移动到借用塔上的n-1个盘子移动到目的塔上，此时B是源塔（上一步为借用塔），A为借用塔（上一步为源塔），参数的位置有变化，但相对位置的意义没有变
	}
}
int main()
{
	printf_s("请输入盘子的个数:\n");
	int n;
	scanf_s("%d", &n);
	char x = 'A', y = 'B', z = 'C';
	printf_s("盘子移动情况如下:\n");
	hanoi(n, x, y, z);
	getchar();
	getchar();
	return 0;
}