KMP算法

前言

今天做一道简单的字符串匹配题目，用了一个naive的方法结果TLE了，虽然最终优化了一下过了但还是不满意。于是复习了一下KMP算法，发现很多以前学过的，理解的东西长时间不看又忘记了，想着正好今天没事，干脆记录一下吧。啰嗦了几句，本文为笔者对KMP算法的一点理解。

KMP算法是一个模式匹配算法（模式串匹配目标串），是由Knuth，Morris，Pratt共同提出的，其特点就是可以在线性时间内完成。它利用一个跳转表，在每次匹配错误的情况下目标串都不用回溯。构造这个跳转表（next数组）就是KMP算法的核心所在。

1. 明确问题

给定两个字符串，一个为m串,也称为目标串，长度为x，一个为n串，也称为模式串，长度为y（x>=y），问题是找出n串在m串中出现的下标。

最容易想到的naive的方法就是遍历m串，一旦发现m[i]==n[0]，就继续比较m[i+1]与n[1]，如果直到n串结束，那自然就找到了。如果中途n[j]!=m[i+j]，则这次匹配是失败的，回溯到m[i+1]继续与n[0]比较。当m串剩余的长度小于n串时可以停止比较，这种算法的复杂度为O(xy)。

2. 子串覆盖

仔细考虑一下，那种naive的算法是有冗余的，考虑下面的情况：
m串：abcabcabcd
n串：abcd
第一次匹配，发现n串和m串前三个元素都相同，第四个不同，只好从m[1]继续，这时n[0]又和m[1]不匹配，到m[2]，发现m[2]和n[0]也不匹配。

KMP算法发现，这两次不匹配其实是可以预知的。为什么呢，因为第一次匹配已经匹配到n[3]了，这意味着m[0,2]==n[0,2]，所以m[1]，m[2]和n[1]，n[2]是相同的，所以这两次比较其实是在与自身比较。这意味着模式串本身蕴藏着一些信息，如果我们早点研究一下模式串，发现n[0]与n[1]，n[2]不匹配那么我们就不用进行上面的尝试了。

这个问题我称之为“子串覆盖”问题。子串覆盖就是说在一个字符串中有两个子串是相同的，如abcdabc，发现abc这个子串出现了两次。正是根据字符串的这个特性，KMP算法构造了跳转表。跳转表是利用字符串这个特性的一种方式，它需要的是寻找字符串中最长的首尾匹配。举个例子：

如图，设这是字符串n，n[0,i]==n[j-i,j]，且没有更长的子串可以做到首尾覆盖。即n[0,i+1]!=n[j-i-1,j]。则对于n[j]而言，它的最长覆盖长度就是i+1，到下标i为止。如果在某次匹配时，n[j+1]与m[k]发生匹配错误，此时我们不需要对m串进行回溯，可以直接把n串[0,i]移到[j-i,j]的位置，让n[i+1]与m[k]比较。

为什么可以这么做？难道n串的0位置就不可能出现在i到j-i之间并且匹配成功吗？看下图：

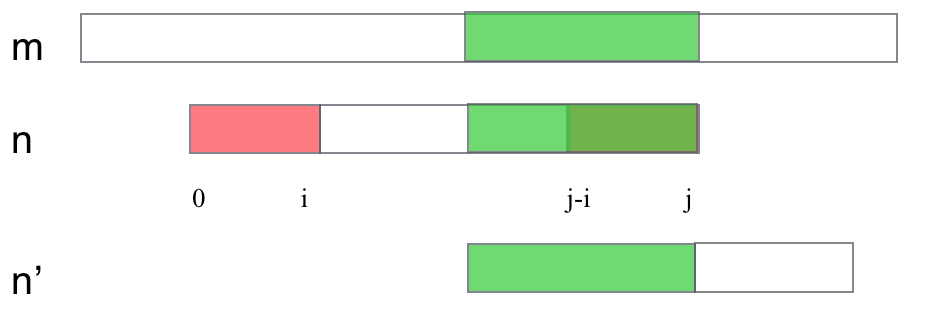
如果n最后移到了n’的位置并且和m串匹配成功（n’中n[0]在i和j-i之间），那么意味着n串中绿色的部分应该是相同的，因为都与m的同一段匹配。显然绿色的部分比红色的长，所以与之前红色的是最长子串覆盖是矛盾的，所以即使最后匹配，n的0下标只可能从红色段开始。

发现了这一点就好办了，我们只要计算出n串中每个字符的最长匹配，记录在一个数组next中，在匹配失败的时候就可以用该数组中的数据，移动n串，而不必再对m串进行回溯了。

3. 计算next值

那么next数组怎么计算呢？其实对于这个数组的具体含义是因人而异的，此处的含义，next[i]，表示的是n[0,i]中最长的子串覆盖，覆盖到的下标。
明确含义后，发现计算next值有两种情况。假设我们要计算next[i]，此时next[i-1]已经知道了，即n[0,next[i-1]]==n[i-1-next[i-1],i-1]。
1、若n[i]==n[next[i-1]+1]，那么next[i]就等于next[i-1]+1
2、若n[i]！=n[next[i-1]+1]，那么需要在n[0,next[i-1]]中继续寻找一个更小的子串。怎么找？与之前类似，我们考察n[next[i-1]]的子串覆盖。
如果n[next[next[i-1]]+1]==n[i]，那么next[i]等于next[next[i-1]]+1，如果不等则重复第二步。
由于next值的含义是最长子串覆盖覆盖的下标，所以若没有子串覆盖其值为-1，n[0]=-1
计算next值的Python代码如下：

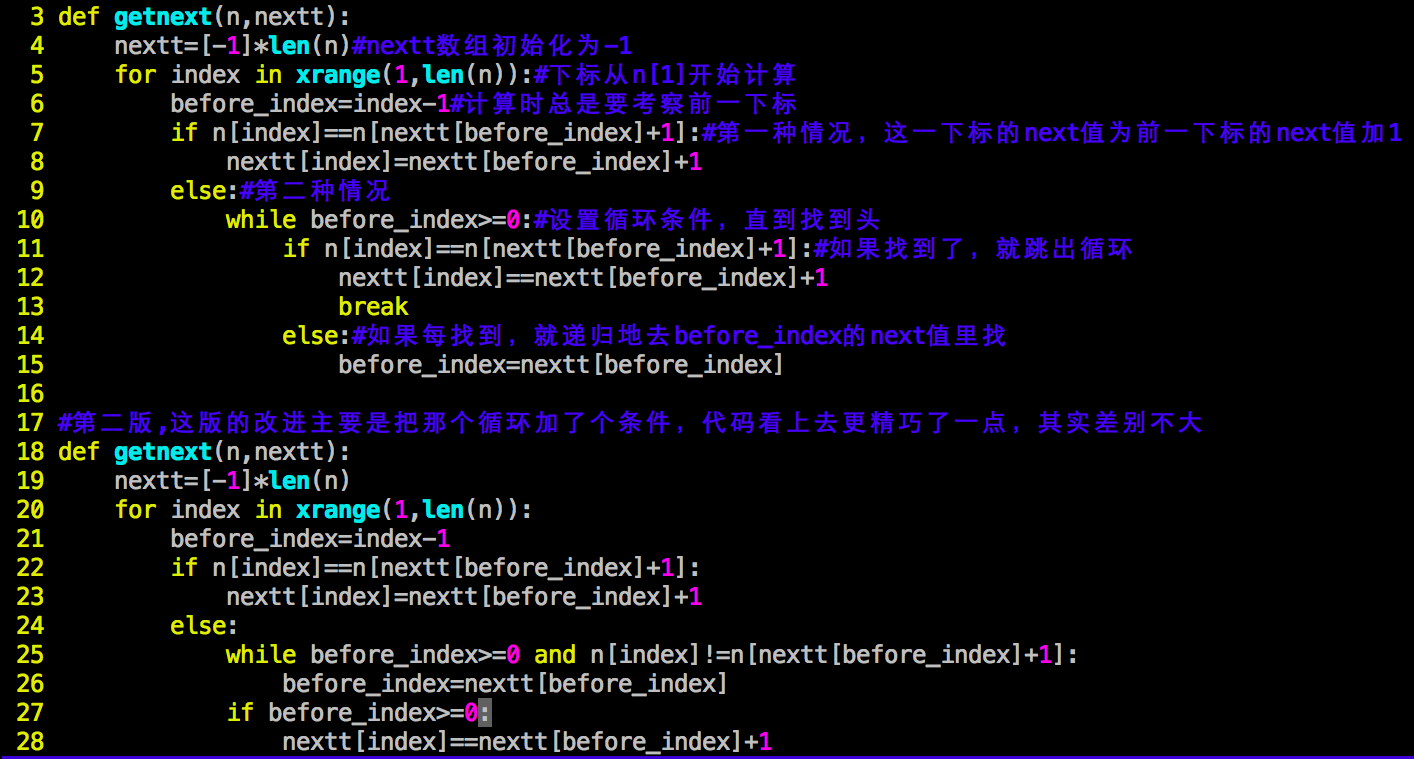
代码中已附注释，不再赘述。其实第一种和第二种情况也是可以进一步合并的，代码可以继续简化，但我觉得这样更利于理解。

4. KMP算法

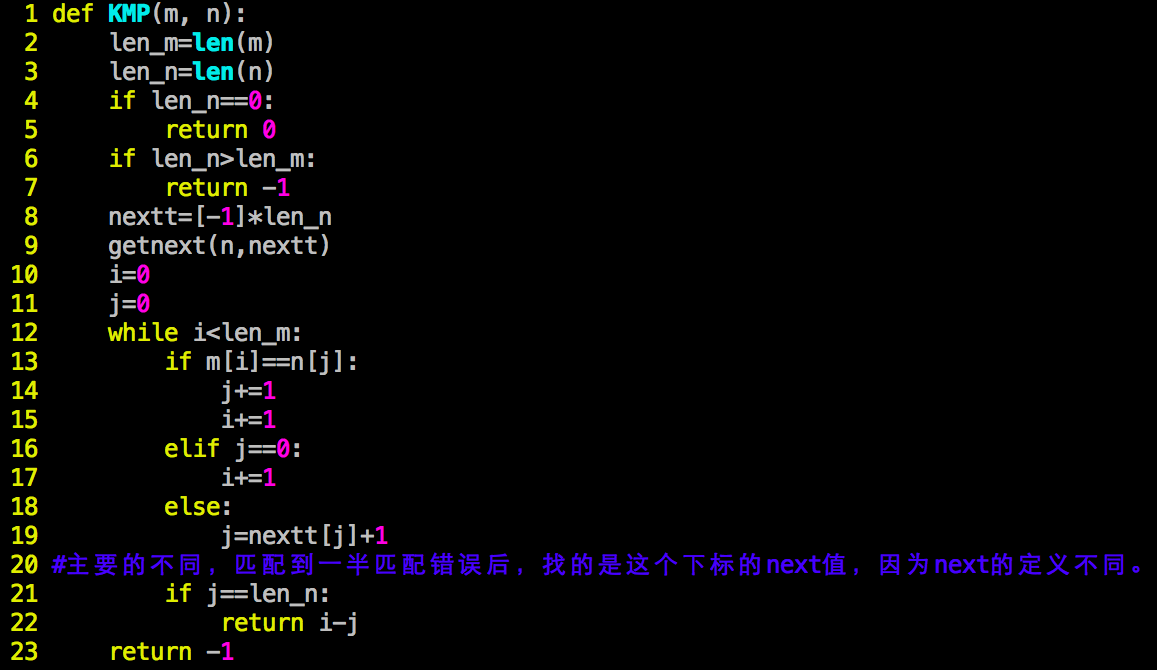
获得了next值之后，再进行kmp算法就简单了，其python代码如下：

可以发现，KMP算法的复杂度是O(x+y)的，比naive得算法有较大提高。

5. 总结

KMP算法其实就是对模式串进行预处理，发现其本身蕴含的信息，然后在匹配的过程中避免了目标串的回溯。KMP算法的精髓就是next数组的构造。但next数组的（细节）具体含义其实是因人而异的。我这里的next[i]是指在n[0,i]之间最长的子串覆盖的下标，这里其实还可以进一步优化。

假设n[i+1]匹配失败，那么n串会从n[next[i]+1]继续匹配，但这里如果n[next[i]+1]与n[i+1]相同的话，那么n[next[i]+1]肯定也会匹配失败的，我们之前的算法并没有考虑这一点。其实我们可以收集这个信息的，因此，还有一套稍微复杂一点的对next数组的理解。

6. 思路2-next定义2

新的定义：next[i]是指在n[0,i-1]中最长的子串覆盖到的下标，并且n[i]!=n[next[i-1]+1]。如果等于的话应该继续考虑n[0,next[i-1]]的子串覆盖。还是以上面出现的一张图为例：

上图中n[j+1]!=n[i+1]，且n[0,i]==n[j-i,j]，此时我们称next[j+1]=i，这样的话如果n[j+1]匹配失败，下一步将n[next[j+1]+1]继续匹配，n[next[j+1]+1]与n[j+1]是确定不相等的，此时这个常识才是更“有意义的”

7. next定义2的求解

这里的next会相对难求一些，我们可以定义f数组，这个数组不考虑是否相等。也就是说，上图中不管n[j+1]与n[i+1]是否相等，f[j+1]=i，这个f数组是比较易求的，方法和前面第一种思路的next是类似的。

在得到f数组后再求next数组就好办多了，也分两种情况：
1、n[j+1]!=n[i+1]，那么next[j+1]=f[j+1]
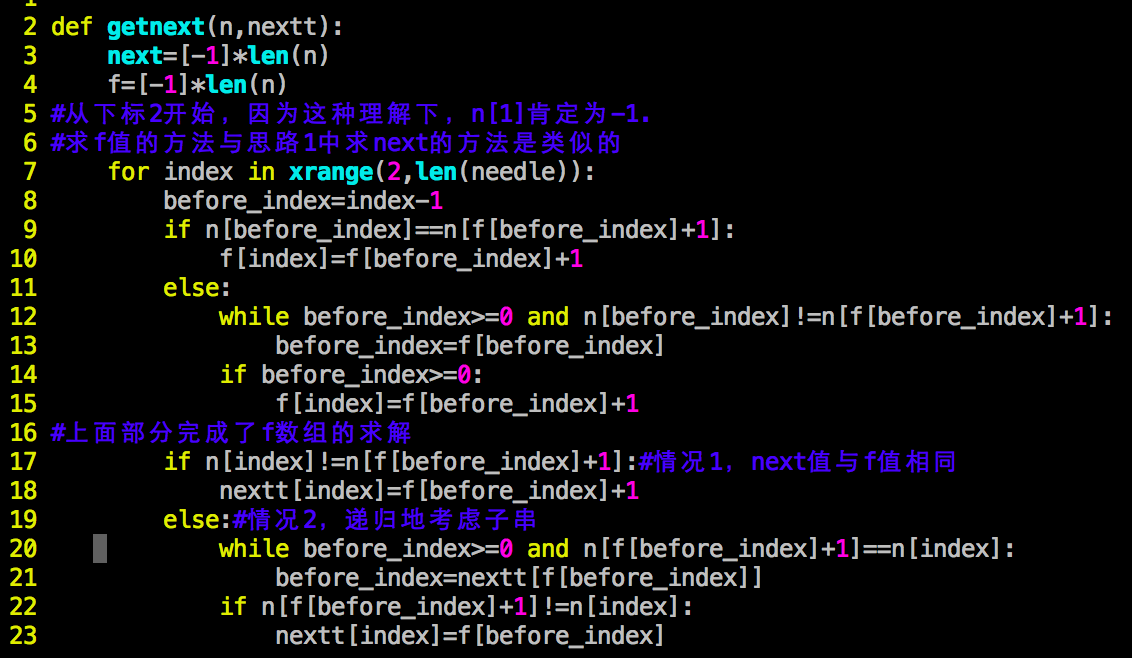
2、n[j+1]==n[i+1]，此时说明把[0,i]移到[j-1,j]的位置是没有意义的。类似的，此时要考虑[0,i]的子串覆盖了，即看n[f[f[j+1]]+1]与n[j+1]是否相等。这种地方递归地考虑子串覆盖的思路与上面的都是类似的。依次下去，直到到达-1，或找到对应的next值。其Python代码如下：

此处的求解比较复杂，应该可以优化，但懒得弄了。。
这样的确获得了更有效的next数组，但其实求解next数组也变得复杂了，所以是否有必要呢。

8. 思路2KMP算法

主题函数是类似的，稍有改变，Python代码如下：

因为next的定义变化，与之前的稍有区别。

9. 总结2

到这里KMP算法基本就结束了，其实我觉得第二种算法比较绕，而且复杂容易出错，和我的思路也挺不对头的，想的时候挺别扭。所以我只是写了一版能过的代码，并没有考虑代码的精简和优化，它应该能有更优雅简洁的形式。以后我用的话应该会用前一种吧，简单也不失效率。