poj 2286 The Rotation Game (迭代加深搜索）

The Rotation Game

Time Limit: 15000MS		Memory Limit: 150000K
Total Submissions: 4643		Accepted: 1545

Description

The rotation game uses a # shaped board, which can hold 24 pieces of square blocks (see Fig.1). The blocks are marked with symbols 1, 2 and 3, with exactly 8 pieces of each kind. 

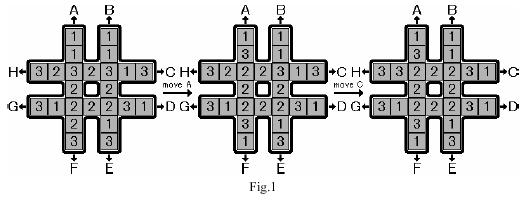
Initially, the blocks are placed on the board randomly. Your task is to move the blocks so that the eight blocks placed in the center square have the same symbol marked. There is only one type of valid move, which is to rotate one of the four lines, each consisting of seven blocks. That is, six blocks in the line are moved towards the head by one block and the head block is moved to the end of the line. The eight possible moves are marked with capital letters A to H. Figure 1 illustrates two consecutive moves, move A and move C from some initial configuration. 

Input

The input consists of no more than 30 test cases. Each test case has only one line that contains 24 numbers, which are the symbols of the blocks in the initial configuration. The rows of blocks are listed from top to bottom. For each row the blocks are listed from left to right. The numbers are separated by spaces. For example, the first test case in the sample input corresponds to the initial configuration in Fig.1. There are no blank lines between cases. There is a line containing a single `0' after the last test case that ends the input. 

Output

For each test case, you must output two lines. The first line contains all the moves needed to reach the final configuration. Each move is a letter, ranging from `A' to `H', and there should not be any spaces between the letters in the line. If no moves are needed, output `No moves needed' instead. In the second line, you must output the symbol of the blocks in the center square after these moves. If there are several possible solutions, you must output the one that uses the least number of moves. If there is still more than one possible solution, you must output the solution that is smallest in dictionary order for the letters of the moves. There is no need to output blank lines between cases. 

Sample Input

1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0

Sample Output

AC
2
DDHH
2

题意：一个#型的棋盘，上面有1、2、3各8个，要求通过8种操作使得最后中间的八个格子数字相同。

感想：开始用bfs  尝试各种判重  要么超时 要么超内存  ╮(╯▽╰)╭

思路：这题要用IDA*   以前没见过  被坑也是正常的

本题若用广搜，空间需求量非常大，空间不足，而且判重也挺复杂的。深搜的话，深度很难控制，容易超时。这个时候就要用到迭代加深的深搜方法。
所谓迭代加深，就是在深度无上限的情况下，先预估一个深度（尽量小）进行搜索，如果没有找到解，再逐步放大深度搜索。这种方法虽然会导致重复的遍历 某些结点，但是由于搜索的复杂度是呈指数级别增加的，所以对于下一层搜索，前面的工作可以忽略不计，因而不会导致时间上的亏空。
这种方法，可以算作是DFS和BFS的结合。适合大树而可行解不是很深的题目。
IDA*对于最优解层数小，每次扩展状态多的时候是一个杀手锏啊。IDA*就是一个加了层数限制depth的DFS，超过了限制就不在搜索下去，如果在当前层数没有搜到目标状态，就加大层数限制depth，这里还只是一个IDA算法，并不是A*的。当然我们可以用A*的估计函数去剪枝，如果当前深度d+h()>depth的时候就可以不再搜索下去了，这样就是IDA*了。
　　对于这道题，我们把状态按输入顺序用一维数组存储，然后对每个元素设定相应的编号：
                  1     2
                  3     4
　　　　　　5  6  7  8  9  10 11
　　　　　　      12    13
　　　　　　14 15 16 17 18 19 20
 　　　　　　     21    22
 　　　　　　     23    24
　　并且把每个操作的相应编号用数组存起来就好处理了：
代码：
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#define maxn 30
using namespace std;

int n,ans,depth;
int a[maxn];
char s[]="ABCDEFGH";
int ffind[8]={7,8,9,12,13,16,17,18};         //　中间的小正方形对应数组下标
int mar[8][7]=               // movearrey  将移动操作对应的数组下标存下来  方便后面操作
{
    1,3,7,12,16,21,23,
    2,4,9,13,18,22,24,
    11,10,9,8,7,6,5,
    20,19,18,17,16,15,14,
    24,22,18,13,9,4,2,
    23,21,16,12,7,3,1,
    14,15,16,17,18,19,20,
    5,6,7,8,9,10,11
};
string path,anss;

void move(int k)              // 移动操作
{
    int i,j,t;
    t=a[mar[k][0]];           // 开始写成了 t=mar[k][0] 找错找了半天  ╮(╯▽╰)╭ 还是小错不断额
    for(j=0;j<6;j++)
    {
        a[mar[k][j]]=a[mar[k][j+1]];
    }
    a[mar[k][6]]=t;
}
void unmove(int k)             // 去除移动操作
{
    int i,j,t;
    t=a[mar[k][6]];
    for(j=6;j>0;j--)
    {
        a[mar[k][j]]=a[mar[k][j-1]];
    }
    a[mar[k][0]]=t;
}
int getdepth()
{
    int i,j,ma=-1;
    int b[4]={0,0,0,0};
    for(i=0;i<8;i++)
    {
        b[a[ffind[i]]]++;
    }
    for(i=1;i<=3;i++)
    {
        if(ma<b[i]) ma=b[i];
    }
    return 8-ma;
}
bool dfs(int k)                     // k-深度
{
    int i,j,h;
    if(k>=depth) return false ;     // 如果深度大于所给定的  直接返回
    for(i=0;i<8;i++)                // 对应的8种操作
    {
        move(i);                    // 移动
        path+=s[i];
        h=getdepth();
        if(h==0)
        {
            anss=path;
            ans=a[7];
            return true ;
        }
        if(k+h<depth&&dfs(k+1)) return true ;     // IDA*的思想 如果当前深度+所需最小移动次数<所限制深度 就不用搜了
        // ps：这样不会漏掉情况 因为如果在这个深度限制内搜不到结果 深度加深后会将开始没考虑的情况补回来
        unmove(i);                                // 回溯 移回来
        path.resize(path.length()-1);
    }
    return false ;
}
int main()
{
    int i,j;
    while(scanf("%d",&n),n)
    {
       a[1]=n;
       for(i=2;i<=24;i++)
       {
           scanf("%d",&a[i]);
       }
       depth=getdepth();
       if(depth==0)
       {
           printf("No moves needed\n%d\n",a[7]);    // 记住这里也要输出ans 
           continue ;
       }
       path="";
       while(!dfs(0))                 // 每次都从深度为0开始
       {
           path="";
           depth++;                   // 限制的深度依次增加
       }
       cout<<anss;
       printf("\n%d\n",ans);
    }
    return 0;
}