参考:
八大排序算法
外部排序
三种线性排序算法 计数排序、桶排序与基数排序
浅谈排序算法实现 (计数排序、基数排序)
堆排序时间复杂度的理解
快速排序及优化
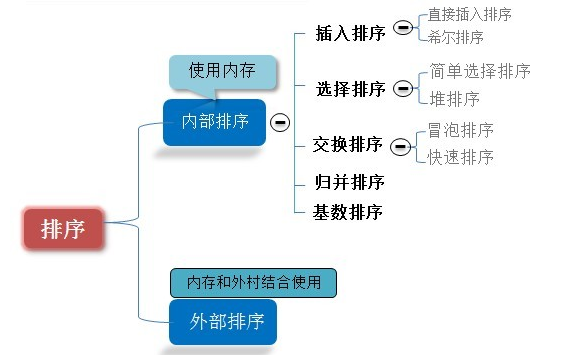
排序分为内部排序与外部排序。
- 内部排序:数据比较少,直接在内存中进行排序
- 外部排序:大量数据排序,待排的数据保存在外存储器上(比如硬盘),带排序文件无法一次装入内存,需要在内存与硬盘之间进行多次数据交换,以达到排序整个文件的目的
这里主要分析内部排序的复杂度以及是否稳定。这里一些内部排序的实现
快排是目前内部排序比较好的方法,当排序关键字是随机分布时,快排的平均时间最短。
插入排序
1,直接插入排序
假定前面元素都是有序的,待插入元素与前面有序元素进行比较,找到插入节点。
效率分析:
对于每个带插入元素都要与前面有序元素比较,比较次数不同导致该算法有最坏情况和最优情况。最优情况为有序 复杂度为O(n);最坏情况逆序:O(n^2)。平均时间复杂度:O(n^2)
对于部分有序数组,插入排序十分高效。
插入排序的复杂度是数组中逆序对的个数。
稳定性:插入排序是稳定的。
2,希尔排序
先将整个待排记录分割成若干序列分别进行直接插入排序,待整个记录基本有序时,再对全体记录进行直接插入排序。
- 选择一个增量序列 t1,t2,…,tk,其中ti>tj,tk=1 (ex:d={n/2,n/4,n/8,..,1});
- 按增量序列个数k,对序列进行k 趟排序;
- 每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
示例:{ 49 , 38 , 65 , 97 , 76 , 13 , 27 , 49 , 55 , 4 }
长度n=10
则增量序列可以是{ 5,2,1 }
第一趟排序,步长为 5
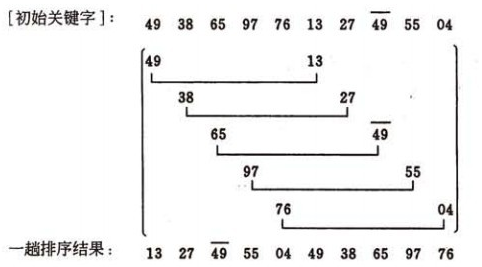
第二趟排序,步长为 2
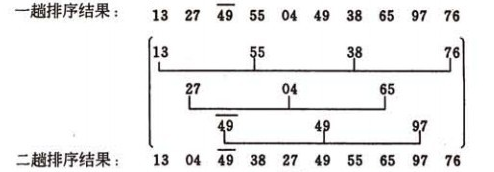
第三趟排序,步长为1
希尔排序是按照不同步长对元素进行插入排序,刚开始元素很无序的时候,步长最大,每一趟排序需要的个数很少,但数据项的距离很长;步长减小时,每一趟需要排序的数据增多,但是元素基本有序,已经接近于他们的最终位置。插入排序对基本有序的序列效率很高。所以希尔排序的时间复杂度会比O(n^2) 好点。
效率:
增量的选取不同,时间复杂度也不同。例如希尔增量时间复杂度为O(n^2),Hibbard增量的时间复杂度为O(n^1.5),希尔排序的时间复杂度下界是:n*log(2n),要比快排的n*log(n) 慢。但是比O(n^2) 算法快得多
一次插入排序不会改变元素的相对位置,但是多次插入会改变元素的相对位置,因此希尔排序是不稳定的算法。
选择排序
3,简单的选择排序
每一趟选出后面最小的值。
没有最优最差情况之分,复杂度都是O(n^2)
不稳定,因为有前后的元素交换。:比如 5 8 5 2 9,第一趟 最小元素是 2 ,2 会和第一个 5 交换,此时破坏了稳定性。
4,简单选择排序的改进
二元选择排序,每趟确定一个最大值,一个最小值。从而减少排序所需的循环次数
5,堆排序
初始时把数组看成一颗顺序存储的二叉树,然后调整元素位置称为一颗最大(最小)堆。
复杂度:
堆排序的时间主要消耗在初始构建堆和重建堆时的反复筛选上。
N个节点,高度为log(n)+1,建堆时,有1/2 的元素向下比较了一次,1/4的元素向下比较了2次,,,1/(2^K) 的元素比较了K次(K=logn,表示层数)
则建堆过程中比较了
建堆时间复杂度O(n)。
正式排序时,第i 次取堆顶元素+重新建堆 O(log2n),需要有(n-1)次重建堆,所以
堆排序时间复杂度为 T(n) <= O(n) + (n - 1)*O(log2(n)), (由于n的减小,后面的O(log2(n))中的n也会减小,所以这里用小于等于号 )。
T(n) =O(nlog2(n)).
稳定性:
取出元素时,堆顶与堆底元素跳跃性互换,肯定是不稳定排序。
交换排序
6.冒泡排序
两两交换,交换的次数是数组中逆序对的个数。
时间复杂度为O(n^2),稳定排序。
改进:
设置一个flag ,发生交换,flag设为true。如果某一趟没有发生交换,说明排序已经完成,不再继续比较
7,快速排序
一趟之后找到某个元素排序好的正确位置。
但是当元素有序时,快排就会退化成冒泡排序了,复杂度O(n^2)。
改进:
- 基数选择随机化,当数组有序时,这种方法可以避免O(n^2),但是由于随机产生器也消耗时间,当数组随机时,性能反而会下降
- 在已经排好的数组上,插入排序时间复杂度是O(n),并且插入排序在小数组上非常高效。当快排递归子序列规模足够小时,使用插入排序。判断子序列长度是否小于某个值,使用插入排序
- 随机数产生器选择基数会带来很大开销,作用是将数组划分的均匀一些。可以使用其他方案代替
- 选取方法是先从数组的开头、结尾和中间选取3个元素,再取这3个元素的中间值作为划分的基准。
- 三个值中选取中间值本身带有一定的随机性,因袭能够很好的处理随机数据。对于最坏情况,也保障至少会有一个值放入大于或小于基数的数组中去了。
- 但是对于大数组来说,先从数组中分三次取样,每次取三个数,三个样品各取出中数,然后从这三个中数当中再取出一个中数作为pivot,也就是median-of-medians。取样也不是乱来,分别是在左端点、中点和右端点取样。
- 对于数组中重复值的问题,使等于基数的重复值不再才遇到下次划分
时间复杂度O(nlog(n)),最坏情况下O(n^2),不稳定
8,归并排序
拆分成若干子序列,子序列有序之后再合并子序列。
线性排序算法
基于比较的排序算法不能突破O(nlog(n)),而非基于比较的排序可以突破O(nlog(n))的时间限制。
线性的排序算法:
- 计数排序 —稳定排序算法,可以用于桶排序
- 桶排序
- 基数排序
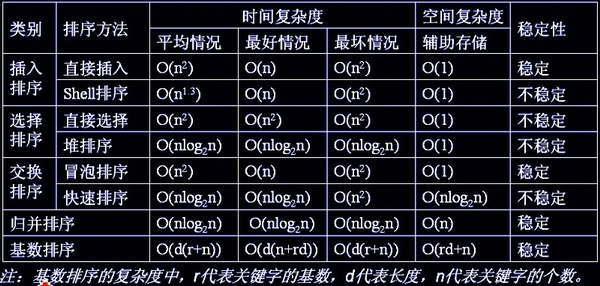
各种排序算法时间复杂度,稳定性比较:










 本文介绍了常见的内部排序算法,包括直接插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序等,并分析了它们的时间复杂度和稳定性。同时,还讨论了几种线性排序算法,如计数排序、桶排序与基数排序。
本文介绍了常见的内部排序算法,包括直接插入排序、希尔排序、选择排序、堆排序、冒泡排序、快速排序、归并排序等,并分析了它们的时间复杂度和稳定性。同时,还讨论了几种线性排序算法,如计数排序、桶排序与基数排序。

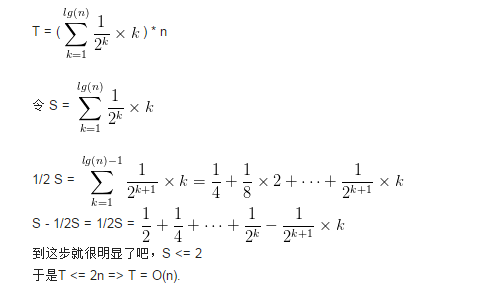














 2838
2838

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








