算法导论 2.1-4

题目

有两个各存放在数组A和B中的n位二进制整数，考虑他们的相加问题。（翻译的够烂）两个整数的和存放在有n+1个元素的数组C中，请给出这个问题的形式化描述，并给出伪代码。

分析

考虑两个1位二进制数a和b，假设它们的和c是个2位二进制数，c[1]=a 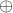b，c[2]=(a+b)/2=(a+b)>>1。

在考虑两个2位二进制数 和 ，它们的和是个3位二进制数 ；

当第一位相加时，先计算进位位c2=(a1+b1)>>1，再计算低位c1=a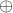1 b1；

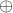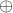当第二位相加时，先计算进位位c3=(a2+b2+c2)>>1，再计算低位c2=a2 b2 c2

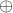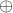以此方法，若c1初始化为0，则各位计算的 =(an+bn+cn)>>1，cn=an bn cn

形式化描述

循环不变式：在循环的每次迭代开始前，c[1...i]保存着a[1...i-1]和b[1...i-1]相加的和。

证明：

初始化：在循环的第一次迭代开始前，此时i=1，c[i]=0。人为给两个规定——1.a[1...0]和b[1...0]不包含任何元素；2.0位二进制数相加得0。在这两个约束下显然c[1]保存着a[1...0]和b[1...0]相加的和。不变式成立。

保持：若循环的某次迭代开始前不变式成立，假设此时i=k，根据不变式，c[1...k]保存着a[1..k-1和]b[1..k-1]相加的和；此次迭代执行，执行的结果就是c[1...k+1]保存着a[1..k]和b[1..k]相加的和；下一次迭代开始前，此时i=k+1，由上次迭代的执行结果知c[1...k+1]保存着a[1..k]和b[1..k]相加的和，即c[1...i]保存着a[1..i-1]和b[1..i-1]相加的和。不变式成立。

终止：循环的迭代终止时，i=n+1，将循环不变式中的i替换为n+1，即c[1...n+1]保存着a[1..n]和b[1..n]相加的和。而a[1..n]和b[1..n]就是完整的两个二进制数，所以不变式成立。

伪代码

ADD-BIN(c, a, b, n)

1 c[1]=0

2     for i <- 1 to n

3         do c[i+1] = (a[i]+b[i]+c[i])>>1

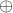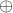4               c[i] = a[i] b[i] c[i]

代码

def addbin_none(c,a,b,n):
    c[0] = 0
    for i in range(0,n):
        c[i+1]=(a[i]+b[i]+c[i])/2
        c[i]=a[i]^b[i]^c[i]