1.2 过程与它们所产生的计算
我们需要看清各种不同种类的过程会产生什么样的计算过程,这样才能构造可靠的程序。一个过程也就是一种模式,它描述了一个计算过程的局部演化方式,描述了这一计算过程中的每个步骤是怎样基于前面的步骤建立起来的,然后做出一些有关这一计算过程的整体或全局行为的论断。
1.2.1 线性的递归和迭代
阶乘的两种方式:
线性递归:
(define (factorial n)
(if (= n 1)
1
(* n (factorial (- n 1)))))线性迭代:
(define (fact-iter product counter max-count)
(if (> counter max-count)
product
(fact-iter (* counter product)
(+ counter 1)
max-count)))
(define (factorial n) (fact-iter 1 1 n))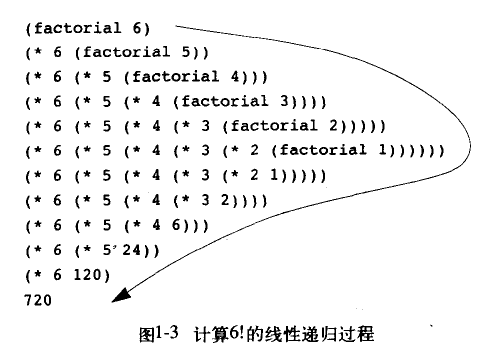
如上图所示,线性递归的代换模型是一种先逐步展开后收缩的形状,在展开阶段构造起一个推迟进行的操作所形成的链条,收缩阶段为这些运算的实际执行。解释器需要在计算过程中保存将来要执行的操作的轨迹,而例子中的运算链条的长度正比于n,是一个线性递归过程。
线性迭代的代换模型则是没有任何的增长或者收缩,对于任意的n,计算的每一步需要保存的东西就是三个变量的值。迭代过程就是这种其状态可以用恒定数目的状态变量描述的计算过程,与此同时又存在一套固定的规则,描述计算过程从一个状态进入下一个新的状态后这些状态变量的更新方式,并且存在某种终止状态,当到达这些终止状态时计算过程终止。在这个例子中计算的迭代次数随n线性增长,是一个线性迭代过程。
由于迭代的计算过程只需要固定数目的状态变量即可描述一个状态,当中止这一过程只需要保存好这几个变量即可,所以保存环境很方便。而递归的计算过程在保存某一中间状态时则需要更多的资源来保存一些“隐含”信息,递归的次数越多,信息量越大。
线性迭代过程的那段代码,从语法上是属于递归过程,而且是尾递归,即递归过程fact-iter将产生一个迭代的计算过程。当然,在C语言等高级语言中,迭代一般使用的是for、while、do while等循环结构,然后在其中设置一些状态变量和转换模式、终止条件,这是包含在一个函数体内的。而若是在C中仿照scheme的代码写成的函数,那么虽然计算过程是迭代的,但是实际上内存的消耗与函数的递归深度成正比,除非其解释器实现了尾递归优化。
附加知识:函数调用另一个函数的过程(C、C++)
1、调用者函数把被调函数所需要的参数计算出来并按照与被调函数的形参顺序相反的顺序压入栈中,即:从右向左依次把被调函数所需要的参数压入栈;2、调用者函数使用call指令调用被调函数,并把call指令的下一条指令的地址(saved PC)当成返回地址压入栈中(这个压栈操作隐含在call指令中);
3、在被调函数中,被调函数会先保存调用者函数的栈底地址(push ebp),然后再将被调函数的栈底地址设置为调用者函数的栈顶地址(mov ebp,esp);
4、在被调函数中,从ebp的位置处开始存放被调函数中的局部变量和临时变量,并且这些变量的地址按照定义时的顺序依次减小,即:这些变量的地址是按照栈的延伸方向排列的,先定义的变量先入栈,后定义的变量后入栈;
5、在被调函数中,若是调用了函数则按照规则从第一步开始执行。
6、若是被调函数完成,则ebp恢复到M[ebp],通过saved pc进入下一条指令,esp恢复到调用被调函数之前的位置,若被调函数有返回值,则在调用者函数中改动相应的局部变量区域。
其中第1和第2步是调用函数所做的工作,第3步和第4步是被调函数所做的工作。ebp在第3步和第5、6步中改动,esp则在所有步骤中均在变动。
下面看一下斯坦福公开课《编程范式》第10讲关于活动记录的介绍,就比较清楚了,但视频截图不是很清楚...
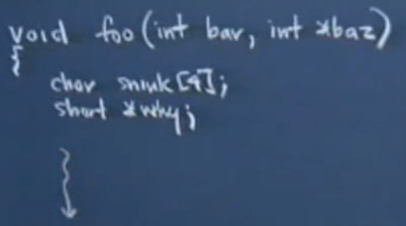
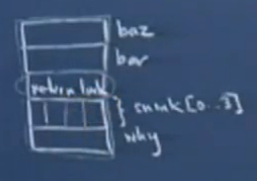
函数foo的传入参数和局部变量在内存中位置很近,如上图的20个字节的结构(从上到下是高地址到低地址)。可以看到snink[4]和why的位置关系:先定义的变量先入栈,后定义的变量后入栈(第4步的方式压入局部变量);传入参数和局部变量的关系:传入参数参数先入栈,局部变量后入栈(第1步和第4步的顺序关系)。
为什么要这样的压入所需实参(baz,bar)而不是相反(bar,baz)呢?(即按照第1步的方式压入参数)
因为C支持可变长度参数形式。如果采用从左到右入栈的顺序,那么第一个参数的位置将是离被调函数最远的那一个,对于不同的调用偏移量可能是不同的,这显然不合适。从右到左入栈的顺序,则第一个参数的位置始终是ebp+8。对于参数列表前面固定位置的参数来说它们的寻址内容是确定的。

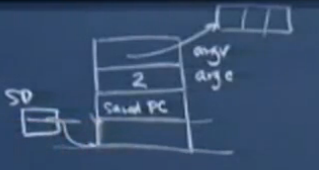
调用函数为main,同样它也有传入参数argc、argv和局部变量i,并且它调用了函数foo。SP(stack pointer)始终指向堆栈的栈顶,saved pc(return link)保存了下一条指令的地址。

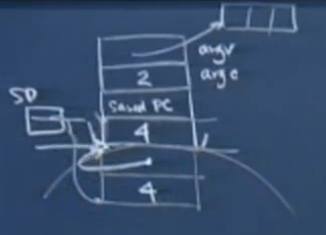
如上图的main函数的模拟汇编代码所示,前两条模拟了“int i=4;”压入局部变量i,后五条压入了传入参数(int 4以及局部变量i的地址)。第三条的sp=sp-8之所以是8个字节是根据foo的形参列表计算出来的。然后foo的传入参数通过寄存器R1和R2中转一下再存入内存中。可以看出来实参i的地址是低于实参&i的地址的。后五条执行的是第1步。
写法a:
R1=M[SP];
R2=SP;
SP=SP-8;
M[SP]=R1;
M[SP+4]=R2;写法b:
R1=M[SP];
R2=SP;
M[SP-4]=R2;
M[SP-8]=R1;
SP=SP-8;以上的两种写法(原汇编代码的3-7条)不知道正不正确,直觉感觉a可能对b应该错,因为觉得push的第一步是硬件操作把sp减掉,不能先操作内存后申请内存。。

接下来在main中call foo,下一步的指令为sp=sp+8。call的时候隐含了将saved pc即“sp=sp+8”的地址压入堆栈的操作,自动有sp=sp-4。执行的是第2步。sp=sp+8则属于第6步,用来释放传入参数的占用内存。rv=0对应于return 0,,rv是专门用来存储被调用函数与调用函数之间的返回值的寄存器,4字节大小。
堆栈的变化:
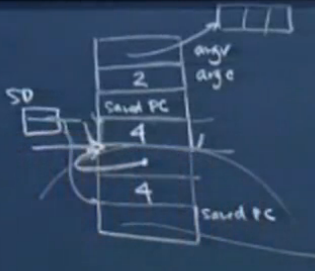
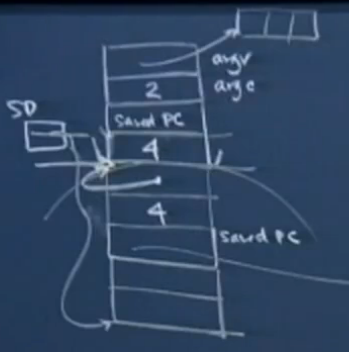
foo:
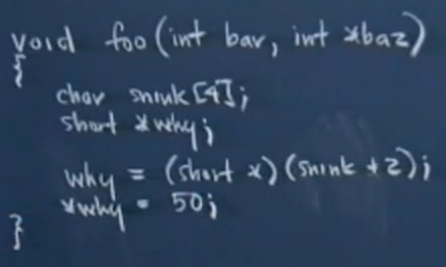
类似main函数,汇编第一条对应foo的1-2句,二-三条对应foo的第3句,四到五条对应foo的第4句,后两条是收尾工作。
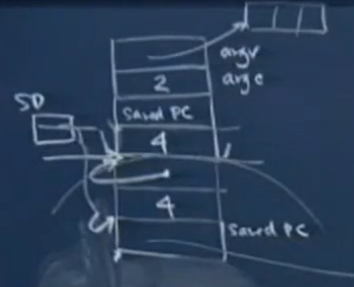
前5条:
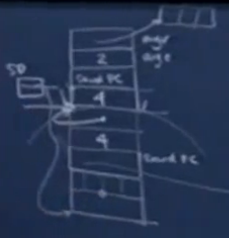
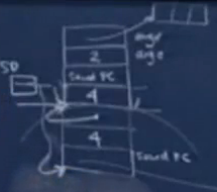
由上图可知函数内部运行时也存在sp的变动,区别于被调函数结束后调用函数在传入参数上的sp=sp+8的变动。RET时M[sp]即为下一条指令的地址,然后自动sp=sp+4。返回后执行的指令为sp=sp+8,即释放传入参数占用的内存。
值得强调的是,传入参数的设置和局部变量的设置是分别由调用函数和被调函数完成的,因为这才是合理可行的。被调函数仅仅有形参,而过程中的实参只能有调用函数生成;被调函数的局部变量的信息只有函数本身才知晓,而黑箱抽象则暗示调用函数不应该知道被调函数的具体细节。saved pc是在call时完成的,ret则干掉了saved pc。
讲到这里,有没有发现少了什么?对了,第3步和第6步的前半部分没有涉及,即ebp没有被提到。这个东西的作用在于,可以用它来定位当前函数在栈上的“坐标”。因为sp实际上随着栈的变化一直在变动,这样想要利用sp来访问到传入参数或者局部变量就比较麻烦。但是ebp在某一个函数的运行过程中是不变的,只有在返回或者调用时ebp才被更新,而且ebp的变动都是在被调用函数内进行的。所以用它加上一定的偏移量可以得到想要的地址。比如M[ebp+4]存着的就是saved pc,M[ebp+8]存着的就是传入参数的第一个参数。而M[ebp]存着的则是调用函数的ebp值,这样被调函数返回时可以得到原有的ebp,继续进行定位。
下面的是阶乘的线性递归函数,当然和scheme的版本一样,对于n<0没有检查。请自行看懂汇编代码的含义并脑补出堆栈的增长、减少以及rv值的变化,或者看视频。。

好了,接下来我仿照上面写一个语法上尾递归的线性迭代的阶乘:
int fact-iter(int n,int tmp)
{
if(n==0) return tmp;
return fact-iter(n-1,tmp*n);
}
int fact(int n)
{
return fact-iter(n,1);
}fact-iter:R1=M[SP+4];
R2=M[SP+8];
BNE R1,0,PC+12;
RV=R2;
RET;
R1=M[SP+4];
R2=M[SP+8];
R2=R1*R2;
R1=R1-1;
SP=SP-8;
M[SP]=R1;
M[SP+4]=R2;
CALL <fact-iter>;
SP=SP+8;
RET;fact:R1=M[SP+4];
SP=SP-8;
M[SP]=R1;
M[SP+4]=1;
CALL <fact-iter>;
SP=SP+8;
RET;尾递归优化就在于,由于过程上实际是迭代的,rv只在最后一步改动,轨迹上每一步只需要一个最新的状态即可,那么之前的所有堆栈层次及其传入参数都是不必要的,并且每层堆栈的传入参数是一样的,那么就不需要在堆栈上继续开辟新的空间了,只需要直接修改调用函数本身的传入参数即可。for循环的变量改变是在局部变量内,而尾递归优化则是在传入参数上的改动,避免了递归产生的内存开销。
优化后的汇编代码如下:
fact-iter:R1=M[SP+4];
R2=M[SP+8];
BNE R1,0,PC+12;
RV=R2;
RET;
R1=M[SP+4];
R2=M[SP+8];
R2=R1*R2;
R1=R1-1;
JMP fact-iter;1.2.2 树形递归
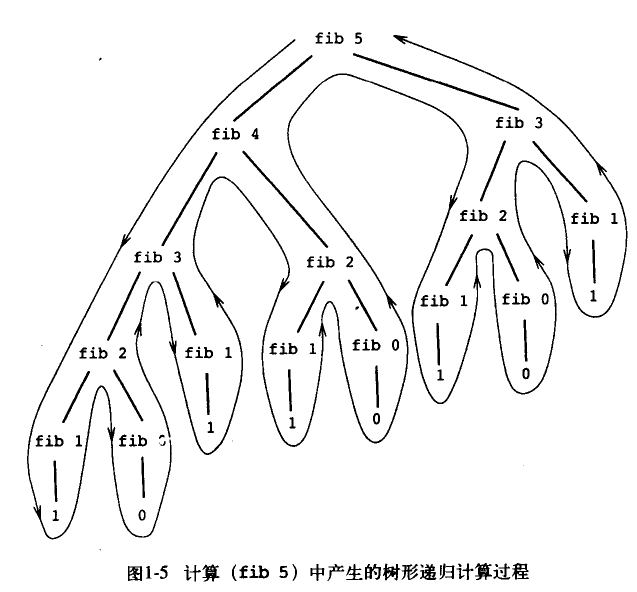
斐波那契数列,若由其定义写出的代码就是树形递归:
(define (fib n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fib (- n 1)) (fib (- n 2))))))由图可知这里面充满了重复计算,计算步骤数随着n的增长呈指数级增长。空间需求则随着n线性增长,因为栈的最大深度就是这个树的高度。
而斐波那契的递归版本在时间复杂度上则是线性的:
(define (fib n) (fib-iter 1 0 n))
(define (fib-iter a b count)
(if (= count 0)
0
(fib-iter (+ a b) a (- count 1))))1.2.3 增长的阶
即算法复杂度
1.2.4 求幂
线性递归:
(define (expt b n)
(if (= n 0)
1
(* b (expt b (- n 1)))))(define (expt b n) (expt-iter b n 1))
(define (expt-iter b counter product)
(if (= counter 0)
product
(expt-iter b
(- counter 1)
(* b product))))(define (even? n) (= (remainder n 2) 0))
(define (square n) (* n n))
(define (fast-expt b n)
(cond ((= n 0) 1)
((even? n) (square (fast-expt b (/ n 2))))
((else (* b (fast-expt b (- n 1))))))欧几里得算法:反复运用一个归约,如果r是a除以b的余数,那么a和b的公约数正好也是b和r的公约数。GCD(a,b)=GCD(b,r)。
(define (gcd a b)
(if (= b 0)
a
(gcd b (remainder a b))))1.2.6 实例:素数检测
方法一:寻找最小因子,若最小因子为本身则这个数是素数。效率为根号下n。
(define (smallest-divisor n) (find-divisor n 2))
(define (find-divisor n test-divisor)
(cond ((> (square test-divisor) n) n)
((divides? test-divisor n) test-divisor)
(else (find-divisor n (+ test-divisor 1)))))
(define (divides? a b) (= (remainder b a) 0))
(define (prime? n) (= n (smallest-divisor n)))费马小定理:如果n是一个素数,a是小于n的任意正整数,那么a的n次方与a模n同余。
对于一个数n,如果随机取到一个小于它的值a不满足a的n次方取模n不等于a,则这个数必然不是素数。
费马检查就是随着检查越来越多的a值,若是一直符合条件,则它是素数的概率越来越大。效率为指数级。
(define (expmod base exp m)
(cond ((= exp 0) 1)
((even? exp)
(remainder (square (expmod base (/ exp 2) m))
m))
(else (remainder (* base (expmod base (- exp 1) m)) m))))
(define (fermat-test n)
(define (try-it a)
(= (expmod a n n) a))
(try-it (+ 1 (random (- n 1)))))
(define (fast-prime? n times)
(cond ((= times 0) true)
((fermat-test n) (fast-prime? n (- times 1)))
(else false)))


























 258
258

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








