金融业信贷风控算法6-广义线性回归

一. 泊松分布

1.1 泊松分布回顾

泊松分布(Poisson Distribution)
回顾：一个事件在一段时间内随机发生，其服从泊松分布的条件为：
将该时间段（或空间）无限分隔成很多个小的时间段（或空间） ，在这个小的时间段（或空间）内，事件发生的概率非常小，不发生的概率非常大。
在每个小的时间段（或空间）内，事件发生的概率是稳定的且与小的时间段（或空间）成正比。
该事件在不同的小时间段（或空间）里，发生与否相互独立。
则事件在一段时间（或空间）内发生的次数的分布服从泊松分布，对应的概率密度函数为：
Font metrics not found for font: .
此处𝜆=𝐸(𝑌)=𝑉𝑎𝑟(𝑌)，即参数𝜆是事件在一段时间（或空间）内发生的次数的期望值，同时也是方差。

1.2 泊松分布的参数估计

对$ {𝑌_1,𝑌_2,…,𝑌_𝑛 }~𝑃𝑜𝑖𝑠𝑠𝑜𝑛(𝜆) $，似然函数及极大似然函数分别为：

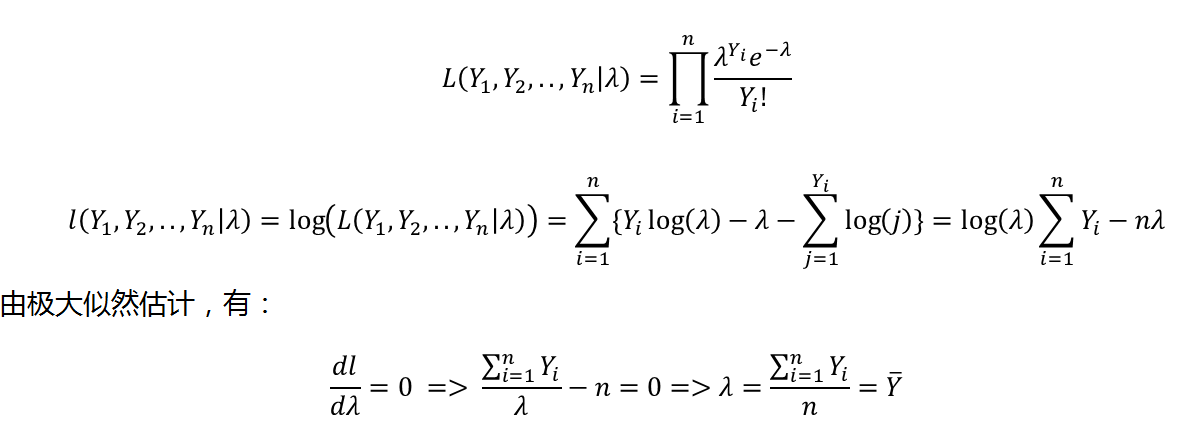
1.3 带速率的泊松分布

进一步地，我们可以结合观察的时间段的长度t以及单位时间内某事件发生的速率𝜆得到带速率的泊松分布：
Font metrics not found for font: .
同样可以使用极大似然估计法得到𝜆的估计。

1.4 参数对分布的影响

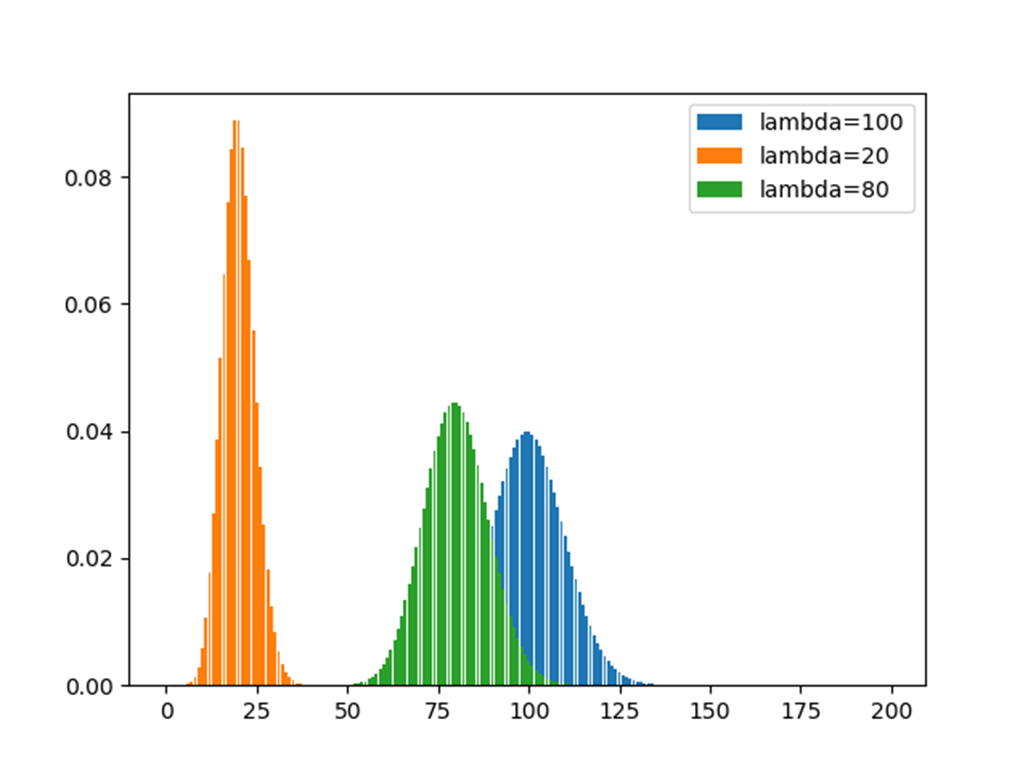
我们考虑以下场景：在上午时间、中午时间和下午时间段内，单位时间内分别有100人、20人和80人到达某窗口，则三个时间段内观察到的人数的分布如左图所示。
很明显，不同的𝜆下，泊松分布的差异很显著的。
我们进一步扩展，
如果能观测到三个时间段的人群的分布，应该如何估计出“时间”对𝜆的影响？
如果𝜆不仅与时间相关，还和其他变量有关联，该如何处理这种数据？

1.5 泊松回归的参数估计

1.6 泊松回归的注意事项

二. 逻辑回归

2.1 logistic变换

在信贷风控业务中，样本间同分布的假设一般是不成立的。对于样本$ {𝑥_𝑖,𝑦_𝑖} $ 而言，其伯努利概率为：
$$P(Y_i=y_i)=p_i^{y_i}(1-p_i{)}^{1-y_i}$$
其中参数$ 𝑝_𝑖 $与特征$𝑥_𝑖$相关。逻辑回归模型就是建立二者的关联。由于参数$𝑝_𝑖$的取值范围是[0,1]的有限区间，一般线性回归
Font metrics not found for font: .
无法保证$p_i$取值的有限性，所以引入下面的logistic变换（所用函数也称为sigmoid函数）：
$$f(x)=\frac{exp(x)}{1+exp(x)}$$

𝑓(𝑥)的特点
单调性，即$f(x_i)>f(x_j)$ 𝑖𝑓 𝑎𝑛𝑑 𝑜𝑛𝑙𝑦 𝑖𝑓 $x_i>x_j$
有界性，即0<𝑓(𝑥)<1 for all x
可导性，即 f^′ (x) 𝑒𝑥𝑖𝑠𝑡 𝑓𝑜𝑟 𝑎𝑙𝑙 𝑥
除此之外，𝑓(𝑥)还有一个计算上的优势，即
$f^{\prime }(x)=f(x)(1-f(x))$

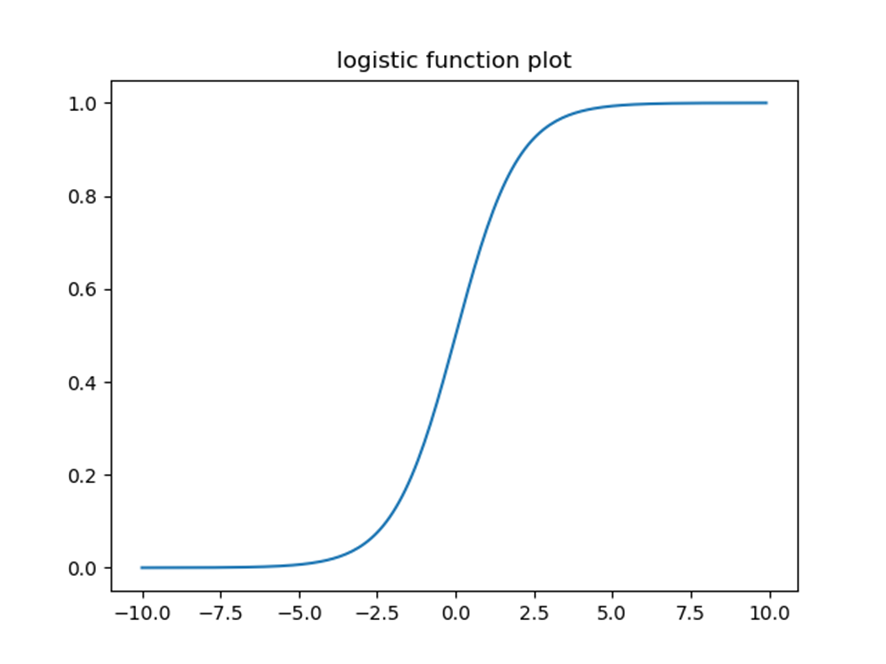
由于logistic变换有上述种种优点，我们将该变换应用在概率的刻画当中：
Font metrics not found for font: .
其中Font metrics not found for font: .分别表示第i个观测值上p个特征的取值和特征的权重。
于是整个逻辑回归模型的形式为：

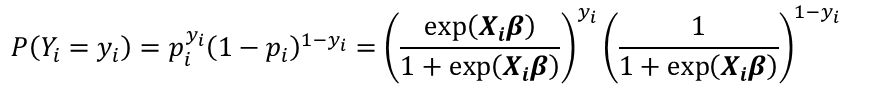
需要注意的是，这里的回归模型是对违约概率做回归，而非对违约状态做回归。

2.2 极大似然估计

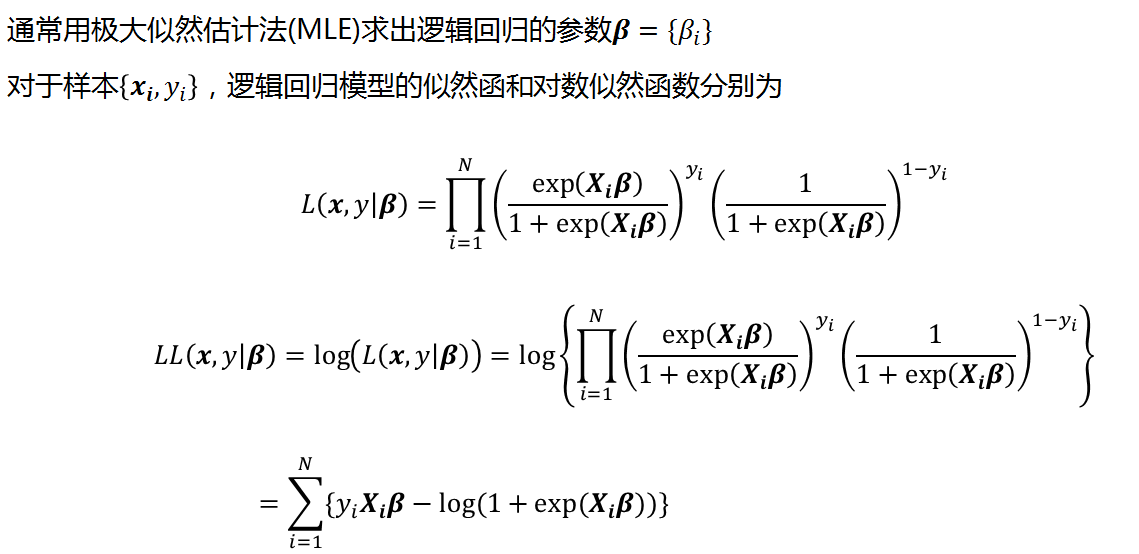
2.3 逻辑回归优缺点

逻辑回归模型的优点：

1. 结构简单：
   变量之间的关系是线性可加关系
2. 可解释性高：
   结构简单；输入变量对目标变量的影响是容易获得的
3. 支持增量训练：
   无需读入全部数据，可增量式地读取数据、训练模型
4. 给出概率而非判别类别：
   模型的结果是估计出属于某一类的概率，可用于更加复杂的决策
5. 工程化相对容易：
   模型的测试、部署、监控、调优等工作相对简单

逻辑回归模型的不足：

1. 预测精度一般
   1）由于模型结构较为简单，导致预测精度不如其他模型
2. 对变量要求高
   1）输入变量需数值类型，需要对非数值变量进行编码
   2）不能容忍缺失值，需要对缺失值做处理
   3）对异常值敏感，需要对异常值做处理
   4）变量尺度差异较大时，容易对模型有影响，需要做变量归一化
   5）变量间的线性相关性对模型有影响，需要做变量挑选或加上正则项

三. 广义线性回归

3.1 指数族分布

前两节介绍的泊松回归与逻辑回归中，变量$\mathbf{X}=X_1,X_2,..,X_n$的作用是线性相加的，即总的效用：
Font metrics not found for font: .
在一般线性回归中，因变量Y的期望值𝜇是𝜂的线性函数：Font metrics not found for font: .，并且Y的分布是期望值为𝜇的正态分布。如果我们将上述2点进行拓展，即Y的分布不局限于正态分布，且Y的期望值𝜇和𝜂的关系为更加一般的链接函数（link function）关系： Font metrics not found for font: .，将会带来什么改变？
指数族分布
如果Y的分布函数形如Font metrics not found for font: .,则称之为指数族分布。正态分布、泊松分布和二项分布等都具有上述形式。
特别地，如果$a(y)=y$，我们称Font metrics not found for font: .具有典型形式（canonical form）。 Font metrics not found for font: .称为Font metrics not found for font: .地自然参数（natural parameter）

不加证明地，我们给出指数族分布的统计特性：

3.2 广义线性回归

有了指数分布族和链接函数后，我们可以构建$\mathbf{X}=X_1,X_2,..,X_n$对Y的广义线性回归模型。
首先$\mathbf{Y}=Y_1,Y_2,\dots ,Y_n$独立同分布于指数分布族的密度函数，因此联合分布

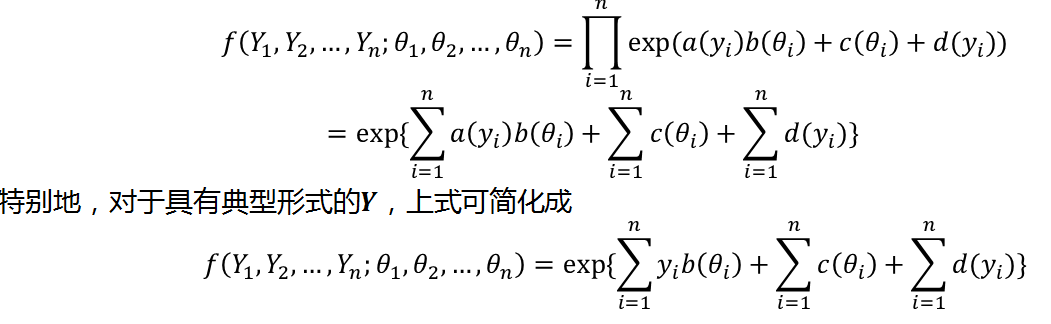
四. 案例

4.1 泊松回归用于预测信贷违约个数

本案例的数据来自Kaggle比赛。我们分别用泊松回归预测自变量与违约个数的关系，用逻辑回归预测自变量与违约概率的关系。
由于原数据中，样本集是单个账户的违约状态和相应的自变量。由于目标变量不是计数类型，我们要对数据进行聚合，统计出发生违约的样本数。在本模型中，我们选取的自变量有CNT_CHILDREN, CODE_GENDER, FLAG_OWN_CAR, FLAG_OWN_REALTY，分别代表子女数、性别、是否有车以及是否有房。建立泊松回归之前，需要做一下数据预处理：

1. 处理缺失值，此处由于只有极少数的样本带有缺失值，因此可采取删除法去除带有缺失值的样本
2. 聚合数据：将样本按照自变量取值进行聚合，计算出自变量每种观测值组合下的违约样本个数
3. 对类别型自变量进行数值编码

类别型变量的数值编码，是指用数值的方式表示非数值型的变量，例如学历、行业、地域等。编码方式可分为有监督和无监督两种。同时，如果类别型变量是有序变量，例如学历、等级等变量，编码结果需要保持原变量的有序性。本案例中使用的类别型自变量‘CODE_GENDER‘, ‘FLAG_OWN_CAR‘, ‘FLAG_OWN_REALTY’全部为无序型变量，我们使用哑变量进行编码。

哑变量编码:
假设类别型变量X有n(n>1)种不同的取值$X_1,X_2,\dots ,X_n$,则构建0-1型的变量 $I_1,I_2,\dots ,I_{(}n-1)$，其取值方式是：如果当前样本中X取值为$X_j,j<n$，则 $I_j=1,I_k=0fork\ne j$。如果当前样本中X取值为$X_n$, 则$I_1=I_2=\dots =I_{(}n-1)=0$
例如，变量CODE_GENDER只有2种取值：M，F，因此可引入哑变量𝐼，如果当前样本取值为M，则I取值为1，否则为0.

完成数据预处理后，将CNT_CHILDREN和另外三个类别型变量对应的哑变量带入到泊松回归中。Python的statsmodels模块中的GLM可以构建包括泊松回归在内的多个广义线性回归模型。

代码:

import pandas as pd
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
from sklearn.linear_model import LogisticRegression


#读取数据，对数据进行筛选。由于原始数据中包含2种不同种类的贷款，我们只选取其中一个进行建模。
mydata = pd.read_csv('D:/learn/application_train_small.csv')
cash_loan = mydata[mydata['NAME_CONTRACT_TYPE'] == 'Cash loans']


#############################################
#############  建立泊松回归模型   #############
#############################################

#作为一个demo，我们只选取数据集中前4个自变量，包含1个数值型变量和3个类别型变量
exog = ['CNT_CHILDREN','CODE_GENDER','FLAG_OWN_CAR','FLAG_OWN_REALTY']

sub_data = mydata[['TARGET']+exog]
#删除有缺失数据的样本
sub_data = sub_data.dropna(axis=0,how='any')
#删除有异常值的样本
sub_data = sub_data[sub_data['CODE_GENDER'] != 'XNA']

#原始数据的样本是账户级别的数据，需要进行分组汇总，计算出分组后每组的违约样本的个数
train_data = sub_data.groupby(exog)['TARGET'].sum().to_frame()
train_data = train_data.reset_index()
#对类别型变量进行哑变量编码
train_data_2 = pd.get_dummies(train_data, columns=['CODE_GENDER','FLAG_OWN_CAR','FLAG_OWN_REALTY']
                              ,prefix=['CODE_GENDER','FLAG_OWN_CAR','FLAG_OWN_REALTY']
                              ,prefix_sep="_",dummy_na=False, drop_first=True)
#增加截距项。注意，此处也可以用自带的函数 sm.add_constant()
train_data_2['intercept'] = [1]*train_data_2.shape[0]
cols = list(train_data_2.columns)
cols.remove('TARGET')

#构建泊松回归模型，因变量是违约样本个数
poisson_regression_model = sm.GLM(train_data_2.TARGET, train_data_2[cols], family=sm.families.Poisson()).fit()
print(poisson_regression_model.summary())
#展现拟合数据和真实数据的误差
result = pd.DataFrame({'prediction': poisson_regression_model.predict(), 'real': train_data_2.TARGET})
result['prediction'] = result.apply(lambda x: int(x['prediction']), axis=1)
result['residual'] =  result.apply(lambda x: np.abs(x['real'] - x['prediction']), axis=1)

chi2.cdf(38000, train_data_2.shape[0]-1-5)
print(result)

输出结果:

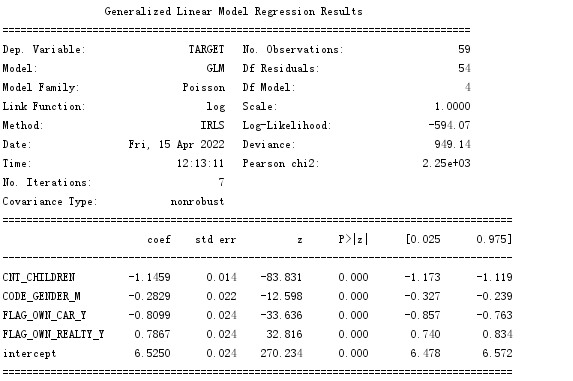
得出结论:
泊松回归的结果显示：
1，所有变量均显著，即所有变量能影响违约样本发生的个数
2，子女越多，发生的违约个数越少
3，男性性别较不容易产生违约
4，有车一族发生违约的个数较少
5，有房一族产生的违约较多。

4.2 逻辑回归用于预测信贷违约概率

在同样的场景下，我们还可以构建广义线性回归模型来预测违约概率。为了探索其他变量的性能，我们重新挑了变量且都为数值类型：AMT_INCOME_TOTAL，AMT_CREDIT，AMT_ANNUITY。
这些变量中，收入AMT_INCOME_TOTAL 和授信额度AMT_CREDIT 会影响到违约行为，但是本身存在一定的相关性，即收入高的人群容易被授予较高的额度，因此我们需要衍生出新的变量：
$$credit-to-income=\frac{AM{T}_{C}REDIT}{AM{T}_{I}NCOM{E}_{T}OTAL}$$
表示授信额度占收入的比例。比例越高，表明还债压力越大，进而发生违约的可能性越高。

新变量的引入带来一个问题：该变量和其他变量的尺度相差很大。数值型变量的尺度（scale）会影响到模型的参数估计，因此需要做归一化的工作以统一不同变量的尺度。本案例中我们采用最小最大化方法：
KaTeX parse error: Expected 'EOF', got '̃' at position 11: {𝑋_𝑖 } ̲̃=\frac{𝑋_𝑖−X_…
其中$X_{m}ax$，$X_{m}in$分别为X的最小、最大的观测值。此外，还需考虑到极端值对模型以及归一化的影响。判断变量是否包含极端值，可以通过箱图（box-plot）的方式，也可以通过以下方式：
$$upper=Q_{75}+(Q_{75}-Q_{25})\times 1.5,lower=Q_{25}-(Q_{75}-Q_{25})\times 1.5$$
如果X的最大、最小值突破了𝑢𝑝𝑝𝑒𝑟和𝑙𝑜𝑤𝑒𝑟，则意味着存在极端值。

上式中， $Q_{25}$和$Q_{75}$分别是变量X的观测值的第25、75个分位点， $Q_{75}$ − $Q_{25}$称为四分位距。参数1.5是四分位距的倍数，也可以换成其他数值。较大的倍数表明对异常值的容忍度高，反之则低。如果存在异常值，则最小最大化公式中的$X_{max}$，$X_{min}$要替换成相应的𝑢𝑝𝑝𝑒𝑟，𝑙𝑜𝑤𝑒𝑟，且归一化后的结果如果超过0或者1的上界，则需要截断成0或1.
例如，变量AMT_ANNUITY的第25、75个分位点分别为18068.625和35694 ，因此四分位距为35694 - 18068.625 = 17625.375 ，$upper=Q_{75}+(Q_{75}-Q_{25})\times 1.5=62132,lower=Q_{25}-(Q_{75}-Q_{25})\times 1.5=-8369$。而变量AMT_ ANNUITY的最大、小值分别为258025.5和1980。可以看出，最大值突破了𝑢𝑝𝑝𝑒𝑟，因此归一化公式里的$X_{max}$应取值62132而非258025.5 。同时原始数值258025.5归一化后远大于1，需要截断成1.

处理完变量的归一化后，使用statsmodels模块中的GLM来构建逻辑回归模型.

python代码:

import pandas as pd
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import chi2
from sklearn.linear_model import LogisticRegression


def Min_Max_Standardize(x):
    [lower, upper] = list(np.percentile(x, [25, 75]))
    d = upper - lower
    ceiling = min(max(x), upper + 1.5*d)
    floor = max(min(x), lower - 1.5*d)

    d2 = ceiling  - floor
    x2 = x.apply(lambda y: max(0,min((ceiling - y)/d2,1)))
    return x2

#读取数据，对数据进行筛选。由于原始数据中包含2种不同种类的贷款，我们只选取其中一个进行建模。
mydata = pd.read_csv('D:/learn/application_train_small.csv')
cash_loan = mydata[mydata['NAME_CONTRACT_TYPE'] == 'Cash loans']

#############################################
#############  建立逻辑回归模型   #############
#############################################
sub_data2 = cash_loan[['TARGET','AMT_INCOME_TOTAL','AMT_CREDIT','AMT_ANNUITY']]
#增加截距项
sub_data2['intercept'] = [1]*sub_data2.shape[0]
sub_data2['credit_to_income'] = sub_data2.apply(lambda x: x.AMT_CREDIT / x.AMT_INCOME_TOTAL, axis = 1)
for feature in ['credit_to_income','AMT_ANNUITY']:
    sub_data2[feature] = Min_Max_Standardize(sub_data2[feature])

exog = ['intercept', 'credit_to_income', 'AMT_ANNUITY']
#构建逻辑回归模型，因变量是违约概率
lr_regression_model = sm.GLM(sub_data2.TARGET, sub_data2[exog], family=sm.families.Binomial()).fit()
print(lr_regression_model.summary())

测试记录:

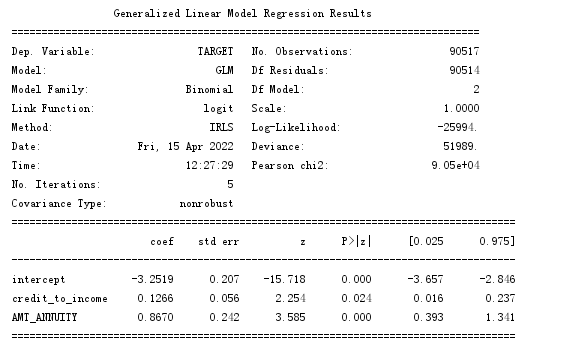
逻辑回归的结果显示：
1，所有变量均显著，即所有变量能影响违约样本发生的概率
2，年金缴纳地越多，越容易发生违约
3，授信比例越高，越容易发生违约。

参考:

1. http://www.dataguru.cn/mycourse.php?mod=intro&lessonid=1701