最近公共祖先LCA问题
小结:
- 暴力
- 二叉查找树(左右子树递归找)
- 非二叉查找树
- 转换为单向链表第一个公共点
- 递归
缺点:适合一次查询,不适合多次,多次复杂度扩大N倍
- Tarjan算法
是一个找强连通分量的算法。dfs+并查集,每次将两个节点对的最近公共祖先的查询保存起来,然后dfs更新一次。
复杂度:O(n + Q), Q为查询个数 - RMQ(没看)
但前面暴力求a[i,j]最小值的位子可以考虑一下: 1. 普通的O(n^3) 2. 动态规划将为O(n^2) - 线段树
用M[i]保存节点i区间的最小值的位置,其中左节点为2*i, 右节点为2*i+1
复杂度<O(N), O(logN)>, 构建O(n),查询O(logn)
问题描述
求有根树的任意两个节点的最近公共祖先
分析与解法
直观的做法,可能是针对是否为二叉查找树分情况讨论,这也是一般人最先想到的思路。除此之外,还有所谓的Tarjan算法、倍增算法、以及转换为RMQ问题(求某段区间的极值)
解法一、暴力对待
1.1 是二叉查找树
算法:
从root开始:
- 如果当前节点t大于u,v,说明u,v都在t的左侧,所以他们的公共祖先必定在t的左子树中,从t的左子树继续查找
- 如果t小于节点u,v.…, 故从t的右子树中继续查找
- 如果当前节点满足 u < t < v, 说明u,v分居在t的两侧,故当前节点t为最近公共祖先
- 如果u是v的祖先,那么返回u的父节点,同理,如果v是u的祖先,返回v的父节点
代码:
//copyright@eriol 2011
//modified by July 2014
public int query(Node t, Node u, Node v) {
int left = u.value;
int right = v.value;
//二叉查找树内,如果左结点大于右结点,不对,交换
if (left > right) {
int temp = left;
left = right;
right = temp;
}
while (true) {
//如果t小于u、v,往t的右子树中查找
if (t.value < left) {
t = t.right;
//如果t大于u、v,往t的左子树中查找
} else if (t.value > right) {
t = t.left;
} else {
return t.value;
}
}
}
1.2 不是二叉查找树
-
我们可以从任何一个节点出发,得到一个到达根节点的单向链表。因此这个问题转换成两个单向链表的第一个公共节点。
-
此外,如果给出根节点,LCA问题可以用递归很快解决。关于树的问题一般都可以转换成递归。
参考代码如下:
node* geteLCA(node* root, node* node1, node* node2)
{
if(root == null)
return null;
if(root == node1 || root == node2)
return root;
node* left = getLCA(root->left, node1, node2);
node* right = getLCA(root->right, node1, node2);
if(left != null && right != null)
return root;
else if(left != null)
return left;
else if(right != null)
return right;
else
return null;
}
然不论是针对普通的二叉树,还是针对二叉查找树,上面的解法有一个很大的弊端就是:如需N 次查询,则总体复杂度会扩大N 倍,故这种暴力解法仅适合一次查询,不适合多次查询。
解法二:Tarjan算法
2.1 Tarjan算法
Tarjan算法是一个在图中寻找强连通分量的算法。算法的基本思想为:任选一节点开始进行深度优先搜索dfs(若深度优先搜索结束后仍有未访问的节点,则再从中任选一点再次进行)。搜索过程中已访问的节点不再访问。搜索树的若干子树构成了图的强连通分量。
对于LCA问题:对于新搜索到的一个节点u,先创建u构成的集合,在对u的每棵子树进行搜索,每搜索完一棵子树,这时候子树中所有的节点的最近公共祖先就是u了。
举例,如下图(不同颜色的节点相当于不同的集合):

假设遍历完10的孩子,要处理关于10的请求了,取根节点到当前正在遍历的节点的路径为关键路径,即1-3-8-10,集合的祖先便是关键路径上距离集合最近的点。
比如:
1,2,5,6为一个集合,祖先为1,集合中点和10的LCA为1
3,7为一个集合,祖先为3,集合中点和10的LCA为3
8,9,11为一个集合,祖先为8,集合中点和10的LCA为8
10,12为一个集合,祖先为10,集合中点和10的LCA为10
得出的结论便是:LCA(u,v)便是根至u的路径上到节点v最近的点。
2.2 Tarjan算法流程
Procedure dfs(u):
begin
设置u号节点的祖先为u
若u的左子树不为空, dfs(u -> 左子树);
若u的右子树不为空,dfs(u -> 右子树);
访问每一条与u相关的询问u,v
若v已经被访问过,则输出v的当前祖先t(t 即u, v的LCA)
标记u为已经访问,将所有u的孩子包括u本身的祖先改为u的父亲
普通的dfs 不能直接解决LCA问题,故Tarjan算法的原理是dfs + 并查集,它每次把两个结点对的最近公共祖先的查询保存起来,然后dfs 更新一次。如此,利用并查集优越的时空复杂度,此算法的时间复杂度可以缩小至O(n+Q),其中,n为数据规模,Q为询问个数。
参考https://www.cnblogs.com/shadowland/p/5872257.html
解法三: 转换为RMQ问题
转换为RMQ问题,用Sparse Table(简称ST)算法解决。
RMQ问题
RMQ问题:
全称为Range Minimum Query,顾名思义,则是区间最值查询,它被用来在数组中查找两个指定索引中最小值的位置。即RMQ相当于给定数组A[0, N-1],找出给定的两个索引如 i、j 间的最小值的位置。
假设我们定义:
假设一个算法预处理时间为 f(n),查询时间为g(n),那么这个算法复杂度的标记为<f(n), g(n)>。我们将用RMQA(i, j) 来表示数组A 中索引i 和 j 之间最小值的位置。 u和v的离树T根结点最远的公共祖先用LCA T(u, v)表示。
举例:
如下图所示,RMQA(2,7 )则表示求数组A中从A[2]~A[7]这段区间中的最小值:
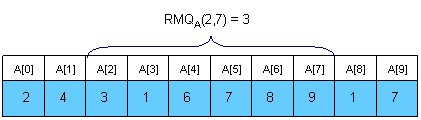
很显然,从上图中,我们可以看出最小值是A[3] = 1,所以也就不难得出最小值的索引值RMQA(2,7) = 3。
RMQ问题解决
1. Trivial algorithm for RMQ
我们对对每一对索引(i, j),将数组中索引i 和 j 之间最小值的位置 RMQA(i, j) 存储在M[0, N-1][0, N-1]表中。
先引出3种计算方法:
- 普通的计算将得到一个<O(N^3), O(1)>的算法。通过一个简单的动态规划,我们可以将复杂度降为<O(N^2,O(1)), 代码如下:
//copyright@
//modified by July 2014
void process1(int M[MAXN][MAXN], int A[MAXN], int N)
{
int i, j;
for (i =0; i < N; i++)
M[i][i] = i;
for (i = 0; i < N; i++)
for (j = i + 1; j < N; j++)
//若前者小于后者,则把后者的索引值付给M[i][j]
if (A[M[i][j - 1]] < A[j])
M[i][j] = M[i][j - 1];
//否则前者的索引值付给M[i][j]
else
M[i][j] = j;
}
- 一个比较有趣的点子是把向量分割成sqrt(N)大小的段。我们将在M[0,sqrt(N)-1]为每一个段保存最小值的位置。如此,M可以很容易的在O(N)时间内预处理。
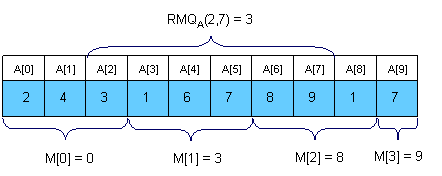
3. 一个更好的方法预处理RMQ 是对2^k 的长度的子数组进行动态规划。我们将使用数组M[0, N-1][0, logN]进行保存,其中M[ i ][ j ] 是以i 开始,长度为 2^j 的子数组的最小值的索引。这就引出了咱们接下来要介绍的Sparse Table (ST) algorithm。
2. Sparse Table(ST) algorithm
…(待看)
解法四:线段树
线段树是一个类似堆的数据结构,可以在基于区间数组上用对数时间进行更新和查询操作。我们用下面递归方式来定义线段树的[i, j]区间:
- 第一个结点将保存区间[i, j]区间的信息
- 如果i<j 左右的孩子结点将保存区间[i, (i+j)/2]和[(i+j)/2+1, j] 的信息
注意具有N个区间元素的线段树的高度为[logN] + 1。下面是区间[0,9]的线段树:
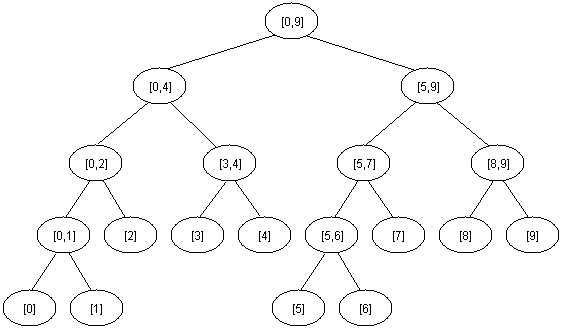
线段树和堆具有相同的结构,因此我们定义x是一个非叶结点,那么左孩子结点为2x,而右孩子结点为2x+1。想要使用线段树解决RMQ问题,我们则要要使用数组 M[1, 2 * 2[logN] + 1],这里M[i]保存结点i区间最小值的位置。初始时M的所有元素为-1。树应当用下面的函数进行初始化(b和e是当前区间的范围):
调用函数时使用node=1, b = 0, e = N -1
void initialize(int node, int b, int e, int M[MAXIND], int A[MAXN], int N)
{
if (b == e)
M[node] = b;
else
{
//compute the values in the left and right subtrees
initialize(2 * node, b, (b + e) / 2, M, A, N);
initialize(2 * node + 1, (b + e) / 2 + 1, e, M, A, N);
//search for the minimum value in the first and
//second half of the interval
if (A[M[2 * node]] <= A[M[2 * node + 1]])
M[node] = M[2 * node];
else
M[node] = M[2 * node + 1];
}
}
现在我们可以开始进行查询了。如果我们想要查找区间[i, j]中的最小值的位置时,我们可以使用下一个简单的函数:
int query(int node, int b, int e, int M[MAXIND], int A[MAXN], int i, int j)
{
int p1, p2;
//if the current interval doesn't intersect
//the query interval return -1
if (i > e || j < b)
return -1;
//if the current interval is included in
//the query interval return M[node]
if (b >= i && e <= j)
return M[node];
//compute the minimum position in the
//left and right part of the interval
p1 = query(2 * node, b, (b + e) / 2, M, A, i, j);
p2 = query(2 * node + 1, (b + e) / 2 + 1, e, M, A, i, j);
//return the position where the overall
//minimum is
if (p1 == -1)
return M[node] = p2;
if (p2 == -1)
return M[node] = p1;
if (A[p1] <= A[p2])
return M[node] = p1;
return M[node] = p2;
}
可以很容易的看出任何查询都可以在O(log N)内完成。注意当我们碰到完整的in/out区间时我们停止了,因此数中的路径最多分裂一次。用线段树我们获得了<O(N),O(logN)>的算法
线段树非常强大,不仅仅是因为它能够用在RMQ上,还因为它是一个非常灵活的数据结构,它能够解决动态版本的RMQ问题和大量的区间搜索问题。
其余解法
除此之外,还有倍增法、重链剖分算法和后序遍历也可以解决该问题。其中,倍增思路相当于层序遍历,逐层或几层跳跃查,查询时间复杂度为O(log n),空间复杂度为nlogn,对于每个节点先存储向上1层2层4层的节点,每个点有depth信息。






















 147
147











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








