(注:本文仅供学习,转载或者拷贝引起的一切后果自负,本文部分内容翻译并参考自:《An Introduction to Mathematical Cryptography》(Jeffrey Hoffstein, Jill Pipher, Joseph H. Silverman))
上一篇介绍了同余公钥密码体制,本篇笔者将介绍另一个经典的密钥体制--背包公钥密码体制。在介绍该问题之前,先介绍下子集和问题。
1、子集和问题
假设在整数域上有集合S={a,b,c,d,e,f.....}和一个整数sum。那么找到集合S的一个子集SubS,该子集满足:该子集中的所有元素相加恰好为sum。比如S={1,2,3,4,5,6,7,8},sum=15,那么我们可以找到其子集SubS={7,8}或者{1,6,8}等等,这样的一个问题就是子集和问题。
子集合问题是NP完备问题(NP-complete problem),其求解是非常困难的(刚刚笔者所给的例子是一种比较简单的情况,读者请不要误以为该问题很好解决)。
我们考虑,子集和问题是否有所谓的特殊情况,而且这种特殊情况我们和容易去求解呢?答案是肯定的。
这里我们将讨论下超递增序列(superincreasing sequence)。即集合S是超递增的,那么什么是超递增序列呢?首先我们给出超递增序列的定义。超递增序列指的是这样的一个集合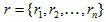

超递增序列具有什么好处呢?由其定义,我们可以知道它具有这样的一个性质: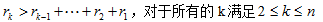
例1:对于超递增序列M={3,11,24,50,115},和Sum=142。求解该子集和问题。
Step 1:142-115=27>0,故115被选中;
Step 2:27-50<0,故50不选;
Step 3:27-24=3>0,故24选中;
Step 4:3-11<0,故11不选;
Step 5:3-3=0,故3选中,算法结束,找到子集。
综上过程,得到的子集为SubS={3,24,115}。验证正确。
那么该如何将这个问题变成一个可用的密码体制?我们只需要将一个超递增序列通过一些运算得到一个非超递增序列(简单的说,就是将超递增序列伪装成非递增序列)。下面我们来介绍由这个问题产生的背包公钥密码体制。
2、背包公钥密码体制
通过上面的介绍,我们对于子集和问题有了一定的认识。那么该如何伪装?
和以前一样,我们先通过一个例子来大概了解下。
例2:有超递增序列r={3,11,24,50,115},Alice选择A=113,B=250。然后Alice通过下面的运算来伪装该超递增序列r。
M=113r (mod 250)={89,243,212,150,245}。显然M不是一个超递增序列了。M就是公钥。
现在Bob要发送一个消息给Alice,这里我们假设消息内容x={1,0,1,0,1}(是一个二元字符串)。然后S=xM=1*89+0*243+1*212+0*150+1*245=546。S即为密文。
Alice接收到Bob发送的密文S后,解密过程如下:
下面给出该密钥体制过程的描述。
(1)Alice:选择一个超递增序列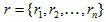
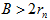
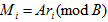
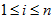

(2)Bob:二元对字符串明文x,用Alice的公钥计算S=x*M。S是密文。
(3)Alice解密:计算
给出该公钥密码体制的JAVA实现。
import java.math.BigDecimal;
import java.math.BigInteger;
public class KnapsackCryptosystems {
private final int MAX = 10;
BigInteger[] SuperSet = new BigInteger[MAX];
BigInteger[] PublicKeySet = new BigInteger[MAX];// 公钥
BigInteger A, B;
public void GenerateSetAndPublicKey() {
SuperSet[0] = (new BigDecimal("10").multiply(new BigDecimal(Math
.random() + "")).add(BigDecimal.ONE)).toBigInteger();
for (int i = 1; i < MAX; i++) {
SuperSet[i] = (SuperSet[i - 1].multiply(new BigInteger("2"))
.add(new BigDecimal("10")
.multiply(new BigDecimal(Math.random() + ""))
.add(BigDecimal.ONE).toBigInteger()));
}
B = (SuperSet[MAX - 1].multiply(new BigInteger("2"))
.add(new BigDecimal("10")
.multiply(new BigDecimal(Math.random() + ""))
.add(BigDecimal.ONE).toBigInteger()));
A = SuperSet[MAX - 1];
while (true) {
A = A.subtract(BigInteger.ONE);
if (B.gcd(A).equals(BigInteger.ONE)) {
break;
}
}
for (int i = 0; i < MAX; i++) {
PublicKeySet[i] = A.multiply(SuperSet[i]).mod(B);
}
}
public BigInteger encrypt(String x) {
BigInteger S = BigInteger.ZERO;
for (int i = x.length(); i < MAX; i++) {
x = x.concat("0");
}
for (int i = 0; i < MAX; i++) {
if (x.charAt(i) == '1')
S = S.add(PublicKeySet[i]);
}
return S;
}
public String decrypt(BigInteger S) {
BigInteger S1;
String x = "";
S1 = A.modInverse(B).multiply(S).mod(B);
int num = MAX;
while (true) {
if (S1.subtract(SuperSet[num - 1]).signum() > 0) {
S1 = S1.subtract(SuperSet[num - 1]);
x = "1".concat(x);
} else if (S1.subtract(SuperSet[num - 1]).signum() == 0) {
x = "1".concat(x);
break;
} else {
x = "0".concat(x);
}
num--;
}
if (num != 0) {
for (int i = 0; i < num - 1; i++)
x = "0".concat(x);
}
return x;
}
public static void main(String args[]) {
KnapsackCryptosystems kc = new KnapsackCryptosystems();
kc.GenerateSetAndPublicKey();
System.out.println("随机产生的公钥:");
System.out.print("(");
for (int i = 0; i < kc.MAX - 1; i++)
System.out.print(kc.PublicKeySet[i] + ",");
System.out.println(kc.PublicKeySet[kc.MAX - 1] + ")");
// 随机产生5组消息
for (int j = 0; j < 5; j++) {
String x = "";
for (int i = 0; i < kc.MAX; i++) {
if (Math.random() < 0.5) {
x = x.concat("1");
} else
x = x.concat("0");
}
// 加密x信息,得到密文S
System.out.println("第" + (j + 1) + "组随机产生的明文: " + x);
String S = kc.encrypt(x).toString();
System.out.println("加密得到的密文:" + S);
System.out.println("解密得到的明文" + kc.decrypt(new BigInteger(S)));
}
}
}
注:上述代码用了随机的明文进行测试,且代码只针对二元字符串进行加密处理,将文本用Huffman编码转换成二进制后分段处理,这里笔者不再实现,本程序仅供参考。
上述代码的运行结果如下:
笔者水平有限,难免存在不足,欢迎批评交流!

























 3995
3995

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








