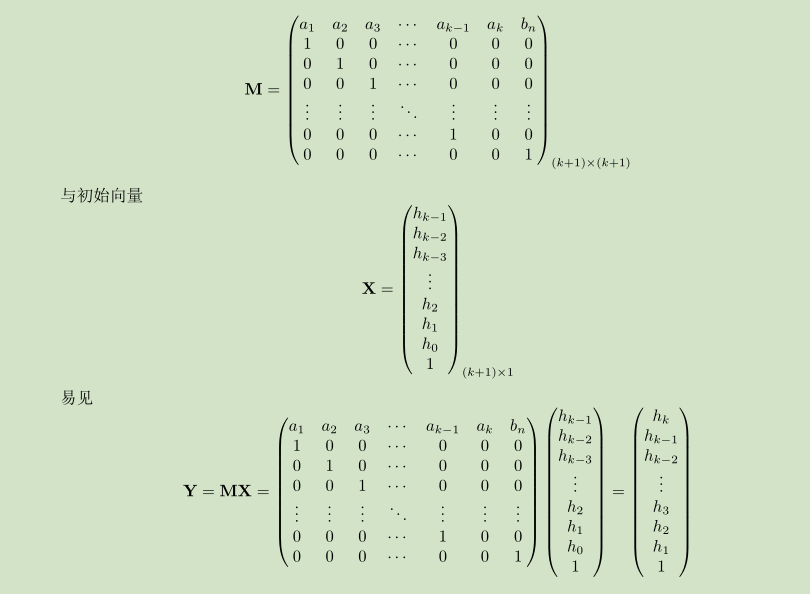
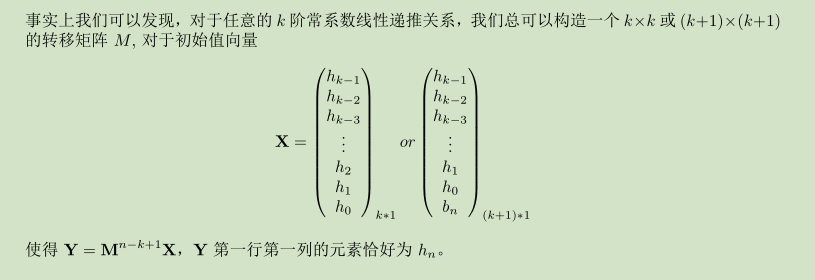
对于一般的具有常系数线性递推关系的递推数列,若需要很快算出某一项的精确值,一般的方法是求出特征方程的解然后解出这个递推关系的通项公式。可是随着递推关系阶数的升高,解特征方程的难度也逐渐增大,甚至在递推关系阶数大于 5 之后,特征方程的次数随之超过 5,根本没有代数解法。本文利用矩阵乘法,提出了一个在 O(k^3 ⌈logn⌈) 的时间复杂度内算出 k 阶常系数线性递推数列第 n 项的精确值的算法,并利用转移矩阵和特征方程的联系,把这个算法的时间复杂度优化到了 O(k^2 ⌈logn⌉).
寻找&星空の孩子
原创,欢迎讨论,转载请注明出出:http://write.blog.csdn.net/postedit/43637741














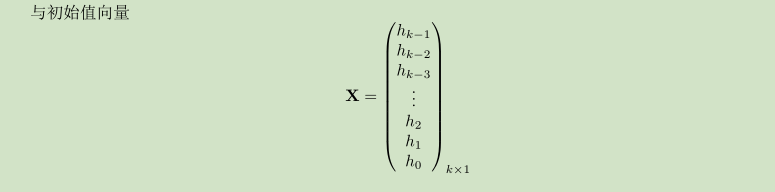





















 225
225

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








