HDU 4790 Just Random (2013ACM/ICPC成都赛区现场赛J题）



题意：给出两个区间[a,b]和[c,d]，分别从这两个区间等概率的抽两个整数x，y，求(x+y)%p=m的概率。

思路：题目要求输出分数，那么分母就是 (d-c+1)*(b-a+1)，分子就是计算满足取出的 x 和 y 的所有组合情况，最容

易想到的就是枚举所有的再加起来。但是数据范围是10的9次方，肯定超时。下面来优化，怎么优化呢，由于 s=x+y，s%p=m，s=p*k+m，s 的值是一个等差数列，所以根据等差数列的性质，知道公差 p，求出满足条件的项，那么前n项和就能求出来了。在这部分优化，会省很多时间。

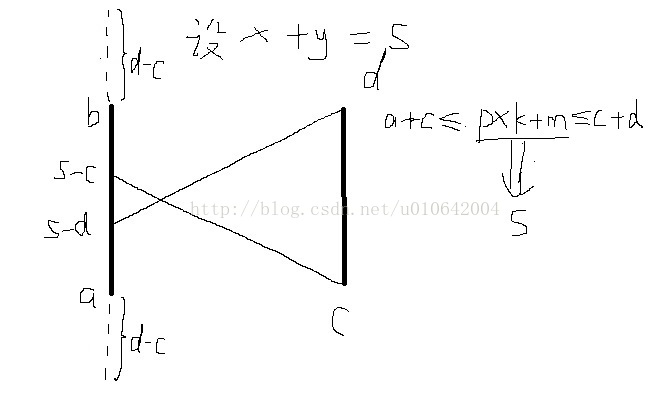
[a,b]，[c,d]两个区间可以看成两个一一映射的关系。如图

易知 x+y=s是一一映射的关系，x=s-y; 取s-y在区间 [a,b] 里的映射，即s-y落在 [a,b]上的范围。

落在 [a,b],共有3种情况（前提： a+c<=s<=b+d  即 s-c>=a , s-d<=b）：

 1. s-d在a的下面，s-c在 [a,b];

 2. 都在 [a,b]内；

 3. s-d在 [a,b]内，s-c在 b 上面；

所以 s 只可能在这三个区间： [a+c,d+a]，[d+a,b+c]，[b+c,b+d]。需要注意 d+a 和 b+c 大小的问题。

然后在分别解出来这三种情况的 s= p*k+m 中的 k 值。三个区间的 s 值是等差数列，所以只需在每个区间里求出两端的 k 值。剩下的就是计算了。

需要注意的是 每个区间的k值 ，k1，k2大小关系，计算结果肯定不能出现负值。还有int和int相乘可能溢出，__int64或long long。求出分子和分母再分别除以公约数即得结果。

AC 代码：

#include<stdio.h>

__int64 mm,n,a,b,c,d,p,m;

//分子和分母化简； 
__int64 gcd(__int64 x,__int64 y)
{
   if(y==0)
   return x;
   return gcd(y,x%y);
}

__int64 max(__int64 x,__int64 y)
{
   return x>y?x:y;
}

__int64 min(__int64 x,__int64 y)
{
   return x<y?x:y;
}

//把每一个k值求出来之后计算满足当前的s值组合数； 
__int64 cal(__int64 k)
{
   __int64 t=p*k+m;
   __int64 x,y,mn,mx;
   x=t-c;
   y=t-d;
   mn=max(a,y);
   mx=min(x,b);
   return max(0,mx-mn+1);
}
   
int main()
{
   int ca=1,T;
   __int64 t,A,B,C,D,gd;
   __int64 k1,k2,k3,k4,k5,k6;//三个区间的k值； 
   scanf("%d",&T);
   while(T--)
   {
      scanf("%I64d%I64d%I64d%I64d%I64d%I64d",&a,&b,&c,&d,&p,&m);
      mm=(d-c+1)*(b-a+1);
      n=0;
      //三个区间共四个端点值； 
      A=a+c;
      B=d+a;
      C=b+c; 
      if(B>C)
      {t=B;B=C;C=t;}
      D=b+d; 
      k1=(A-m)/p; 
      //计算k值； 
      if(p*k1+m<A)
      k1++;
      k2=(B-m)/p;
      if(p*k2+m>=B)
      k2--;
      if(p*k2+m<B)
      k3=k2+1;
      else
      k3=k2;
      k4=(C-m)/p;
      if(p*k4+m>=C)
      k4--;
      if(p*k4+m<C)
      k5=k4+1;
      else
      k5=k4;
      k6=(D-m)/p;
      if(p*k6+m>D)
      k6--;
      //计算三个区间的组合数； 
      if(k2>=k1)
      n+=(cal(k1)+cal(k2))*(k2-k1+1)/2;
      if(k4>=k3)
      n+=(cal(k3)+cal(k4))*(k4-k3+1)/2;
      if(k6>=k5)
      n+=(cal(k5)+cal(k6))*(k6-k5+1)/2;
      if(n==0)
      printf("Case #%d: 0/1\n",ca);
      else
      {
         gd=gcd(n,mm);
         printf("Case #%d: %I64d/%I64d\n",ca,n/gd,mm/gd);
      }
      ca++;
   }
   return 0;
}