Codeforces Round #316 (Div. 2)E. Pig and Palindromes（dp好题）

E. Pig and Palindromes

Peppa the Pig was walking and walked into the forest. What a strange coincidence! The forest has the shape of a rectangle, consisting of n rows and m columns. We enumerate the rows of the rectangle from top to bottom with numbers from 1 to n, and the columns — from left to right with numbers from 1 to m. Let’s denote the cell at the intersection of the r-th row and the c-th column as (r, c).

Initially the pig stands in cell (1, 1), and in the end she wants to be in cell (n, m). Since the pig is in a hurry to get home, she can go from cell (r, c), only to either cell (r + 1, c) or (r, c + 1). She cannot leave the forest.

The forest, where the pig is, is very unusual. Some cells of the forest similar to each other, and some look very different. Peppa enjoys taking pictures and at every step she takes a picture of the cell where she is now. The path through the forest is considered to be beautiful if photographs taken on her way, can be viewed in both forward and in reverse order, showing the same sequence of photos. More formally, the line formed by the cells in order of visiting should be a palindrome (you can read a formal definition of a palindrome in the previous problem).

Count the number of beautiful paths from cell (1, 1) to cell (n, m). Since this number can be very large, determine the remainder after dividing it by 109 + 7.

Input

The first line contains two integers n, m (1 ≤ n, m ≤ 500) — the height and width of the field.

Each of the following n lines contains m lowercase English letters identifying the types of cells of the forest. Identical cells are represented by identical letters, different cells are represented by different letters.

Output

Print a single integer — the number of beautiful paths modulo 109 + 7.
Sample test(s)
Input

3 4
aaab
baaa
abba

Output

3

Note

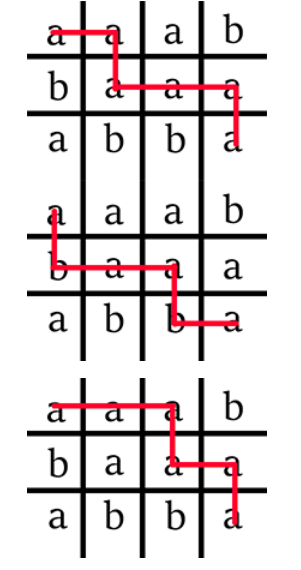
Picture illustrating possibilities for the sample test.

参考自：E. Pig and Palindromes
题意：N*M的字符矩阵，从(1,1)走到(N,M)有多少种方法能使路径上的字符串是回文串
思路：一个点走，相当于两个点分别从（1,1）向下向右走，另一个从(N,M)向上向左走，并且这两个点走的字符必须相同，dp[step][x1][y1][x2][y2]表示走step步，两个点分别到达(x1,y1),(x2,y2)这两个点并且路径上的字符相同的方案数有多少，那么每次按照他们能走的方向递推就行了。还有个问题这样的dp数组是开不下的，首先可以把它写成滚动数组，然后，因为知道起点，步数还有x坐标，y坐标是可以计算出来的，所以可以把y坐标的两维省掉。
于是就是枚举步数和两个x坐标了，还有点需要注意的就是N+M是奇数的时候

#include<bits/stdc++.h>
using namespace std;
const int maxn=510;
const int MOD=1e9+7;
int dp[2][maxn][maxn];
int N,M;
char s[maxn][maxn];
void add(int &x,int y){
    x+=y;
    if(x>=MOD)x-=MOD;
}
int main(){
    scanf("%d%d",&N,&M);
    for(int i=1;i<=N;i++){
        scanf("%s",s[i]+1);
    }
    int cur=0;
    dp[0][1][N]=(s[1][1]==s[N][M]);
    for(int step=1;step<=(M+N-2)/2;step++){
        cur^=1;
        for(int i=0;i<=N;i++){
            for(int j=1;j<=N;j++){
                dp[cur][i][j]=0;
            }
        }
        for(int x1=1;x1<=N&&x1-1<=step;x1++){
            for(int x2=N;x2>=1&&N-x2<=step;x2--){
                int y1=1+step-(x1-1);
                int y2=M-(step-(N-x2));
                if(s[x1][y1]!=s[x2][y2])continue;
                //向左向右
                add(dp[cur][x1][x2],dp[cur^1][x1][x2]);
                //向左向上
                add(dp[cur][x1][x2],dp[cur^1][x1][x2+1]);
                //向下向右
                add(dp[cur][x1][x2],dp[cur^1][x1-1][x2]);
                //向下向上
                add(dp[cur][x1][x2],dp[cur^1][x1-1][x2+1]);
            }
        }
    }
    int ans=0;
    for(int i=1;i<=N;i++){
        add(ans,dp[cur][i][i]);
    }
    if((N+M)%2){
        for(int i=1;i<N;i++){
            add(ans,dp[cur][i][i+1]);
        }
    }
    printf("%d\n",ans);
    return 0;
}