仅仅是本人在观看imooc教程时整理的学习笔记。
教程作者的官方github
https://github.com/liuyubobobo/Play-with-Algorithm-Interview
【动态规划】
【1】定位
对动态规划算法设计思想究竟是什么,有一个深刻的理解。
【2】概述
动态规划是公认的具有艺术性,设计感较强的算法设计思想;
可解决问题的范围非常广泛,非常灵活的算法设计思想;
【3】什么是动态规划
举例:
斐波那契数列 Fibonacci Seqsuence —— 与物理世界有着千丝万缕的关系
f(0)=0 f(1)=1 f(n)=f(n-1)+f(n-2)
举例子:f(5)的递归树:

特点:由递归树可以看出存在大量的重复计算
优化手段:记忆化搜索技巧
优化效果:O(2^n)->O(n)
记忆化搜索-自顶而下的解决问题
实质:在递归的过程中添加记忆化的过程,而递归是自顶而下的解决问题。没有从基本的问题开始解决问题,而是假设基本的问题已经解决掉了。例如在求第n个fib数列时候,已经假设第n-1和n-2个fib数列已经求出来了,我们直接相加得到第n的fib数列。
动态规划-自底而上的解决问题
先解决小数据量下的结果是怎样的也就是先解决最基础的问题,然后层层递推(循环递推),到大数据量下的结果。—— 通常这个过程就叫做动态规划。
维基百科的定义:将原问题拆解成若干子问题,同时保存子问题的答案,使得每个子问题只求解一次,最终获得原问题的答案。
百度百科的定义:动态规划算法与分治法(递归)类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的(会有大量重复)。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。具体的动态规划算法多种多样,但它们具有相同的填表格式。
大多数的动态规划本质都是递归问题,只不过在递归的过程中会存在重叠子问题的过程:

动态规划的本质和记忆化搜索是一样的。通常自下而上的思考问题是比较困难的,反而自上而下的思考问题确实更贴合人类的思维的。所以有时候在使用动态规划的时候,我们可以先自顶向下的思考,然后自底向上的编码实现。【递归结构】——>【记忆化搜索】——>【动态规划】
【4】动态规划问题
分类:
线性动规:拦截导弹,合唱队形,挖地雷,建学校,剑客决斗等;
区域动规:石子合并, 加分二叉树,统计单词个数,炮兵布阵等;
树形动规:贪吃的九头龙,二分查找树,聚会的欢乐,数字三角形等;
背包问题:01背包问题,完全背包问题,分组背包问题,二维背包,装箱问题,挤牛奶
状态与状态转移方程
状态可以简单的看成是一个函数的定义:做什么事
状态转移方程可以理解:怎样做
【6】从例题中学习
例题也有个性
具有明显重叠子结构的递归
没有明显重叠子结构的递归
【70】 Climbing Stairs - 斐波那契数列实例

【记忆化搜索】
#include <iostream>
#include <vector>
using namespace std;
// 记忆化搜索
class Solution {
private:
vector<int> memo;
int calcWays(int n){
//递归结束:爬1阶台阶,或者爬2阶台阶
if( n == 0 || n == 1)
return 1;
//递归计算计算子问题,并保存
if( memo[n] == -1 )
memo[n] = calcWays(n-1) + calcWays(n-2);
return memo[n];
}
public:
int climbStairs(int n) {
memo = vector<int>(n+1,-1);
return calcWays(n);
}
};
int main() {
cout<<Solution().climbStairs(10)<<endl;
return 0;
}【动态规划】
#include <iostream>
#include <vector>
using namespace std;
// 动态规划
class Solution {
public:
int climbStairs(int n) {
vector<int> memo(n+1,-1);
memo[0] = 1;
memo[1] = 1;
for( int i = 2 ; i <= n ; i ++ )
memo[i] = memo[i-1] + memo[i-2];
return memo[n];
}
};
int main() {
cout<<Solution().climbStairs(10)<<endl;
return 0;
}【练习】
【120】Triangle

【64】Minimum Path Sum
【343】 Integer Break
与斐波那契数列无关;
【经验】
在面对一个问题没有思路的时候,应该从暴力解决入手,当然最常见的就是循环暴力,和回溯法(递归),此题我们不知道一个整数可以分割成几个数,没有办法确定要使用几重循环,因此选择回溯法。

【动态规划的特性】
存在重叠子问题
存在最优子结构:通过求解子问题的最优解,可以获得原问题的最优解。正是存在这样的性质,才有递归(原问题与子问题)的。
【经验】
如果将一个问题的递归结构弄清楚之后,如果次递归结构中存在大量的重叠子问题,我们就可以使用动态规划。

【记忆化搜索】
#include <iostream>
#include <vector>
using namespace std;
class Solution {
private:
vector<int> memo;
//将n进行分割(至少分割成两部分),可以获得的最大乘积
int breakInteger( int n ){
if( memo[n] != -1 )
return memo[n];
int res = n;
for( int i = 1 ; i <= n-1 ; i ++ )
//i+(n-i)
res = max( res , i * breakInteger(n-i) );
memo[n] = res;
return res;
}
public:
int integerBreak(int n) {
memo = vector<int>(n+1, -1);
int res = -1;
for( int i = 1 ; i <= n-1 ; i ++ )
res = max( res , i * breakInteger(n-i) );
return res;
}
};
int main() {
cout<<Solution().integerBreak(2)<<endl;
cout<<Solution().integerBreak(10)<<endl;
return 0;
}【动态规划】
#include <iostream>
#include <vector>
using namespace std;
class Solution {
private:
int max3( int a , int b , int c ){
return max(max(a,b),c);
}
public:
int integerBreak(int n) {
//memo[i]表示数字i分割(至少分割成两部分)后得到的最大乘积
vector<int> memo(n+1, -1);
memo[1] = 1;
for( int i = 2 ; i <= n ; i ++ )
//求解memo[i]
for( int j = 1 ; j <= i-1 ; j ++ )
//j+(i-j)
memo[i] = max3( memo[i] , j*(i-j) , j*memo[i-j]);
return memo[n];
}
};
int main() {
cout<<Solution().integerBreak(2)<<endl;
cout<<Solution().integerBreak(3)<<endl;
cout<<Solution().integerBreak(4)<<endl;
cout<<Solution().integerBreak(10)<<endl;
return 0;
}【思考题】
【279】Perfect Squares
【91】Decode Ways
【62】Unique Paths
【63】Unique Paths 2
【198】 House Robber
【状态和状态转移】

【练习题】
【213】House Robber 2
【337】House Robber 3
【309】Best Time to Buy and Sell Stock with Cooldown
经典:背包问题
写在之前的话,为什么要去学习经典问题,因为往往很多问题都会转换为经典的问题,在者我们在经典问题的求解中可以很好地理解算法设计的思路与美感。
01背包
思考的过程
若一时间没有很好的思路,我们不妨按部就班,首先从暴力解法入手。
暴力解法:
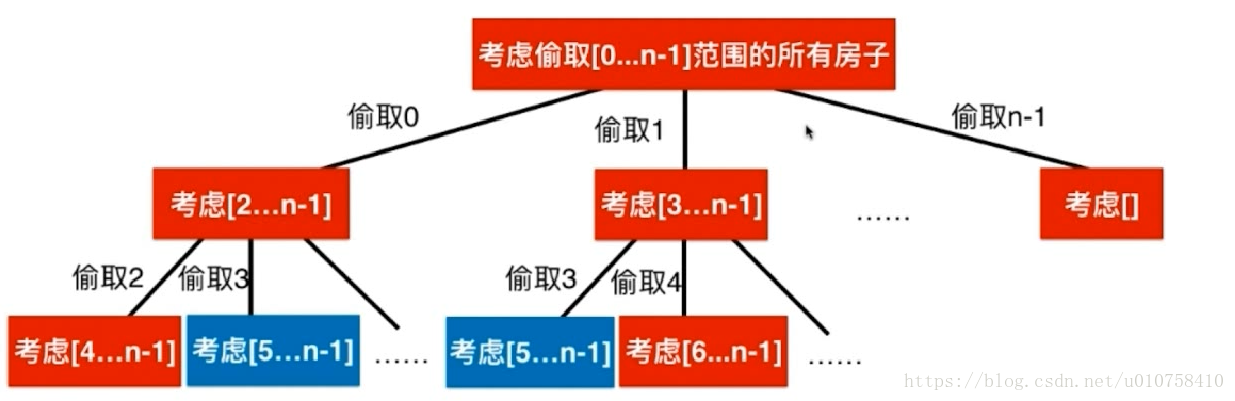
首先从n个物品中选的一些物品放入一个有体积限制的背包内,同时要满足价值最大化。不难发现这是个组合问题,我们可以这么做,首先所有的物品组合求处理(这里一共有2^n种组合,每个物品都有两只中选择,选择放或者不放)。然后在这些组合中进行筛选满足体积限制的组合进行保留,在对这些保留的组合进行价值评估,求得价值最大化的组合。时间复杂的为O((2^n)*n)。组合问题的求解通常用递归暴力解决,递归中如果存在重叠子结构和最优子结构,那么我们可以用记忆化搜索和动态规划的手段进行优化。
在这里对比一下贪心算法:(往往求得的是次优解)
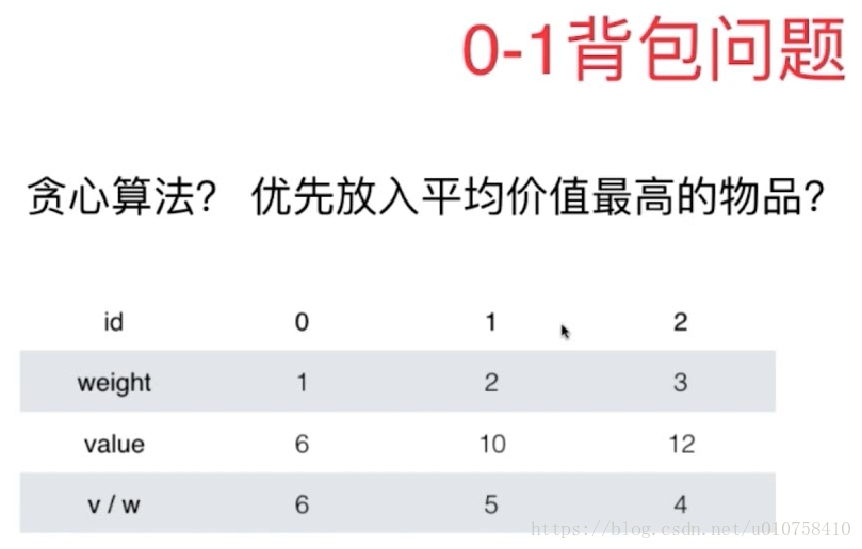
贪心算法的求解是一个次优解,这往往是我们现实生活中的策略

这个例子的最优解

开始求解:明确两个东西,状态是什么,以及状态转移方程是什么
状态:
话句话说:定义一个递归函数,明确这个函数究竟要做什么,包括哪些参数(参数个数,与约束条件有关:(在n个物品中选择,这些物品要满足容量c的限制))
F(n,C)考虑将n个物品放进容量为C的背包,使其价值最大。
状态转移方程:

很多动态规划的问题可以使用类似的思想。
自顶向下的求解
优化:加入记忆化搜索
import java.io.InputStream;
import java.util.Arrays;
import java.util.Scanner;
public class Solution1 {
private int[][] memo;
public int knapsack01(int[] w, int[] v, int C) {
if (w == null || v == null || w.length != v.length)
throw new IllegalArgumentException("Invalid w or v");
if (C < 0)
throw new IllegalArgumentException("C must be greater or equal to zero.");
int n = w.length;
if (n == 0 || C == 0)
return 0;
memo = new int[n][C + 1];
for (int i = 0; i < n; i++) {
Arrays.fill(memo[i], -1);
}
return bestValue(w, v, n - 1, C);
}
// 用 [0...index]的物品,填充容积为c的背包的最大价值
private int bestValue(int[] w, int[] v, int index, int c) {
if (c <= 0 || index < 0)
return 0;
if (memo[index][c] != -1) {
System.out.println("已经保存过了\n");//测试发现,此时已经不存在记忆化
return memo[index][c];
}
int res = bestValue(w, v, index - 1, c);
if (c >= w[index])
res = Math.max(res, v[index] + bestValue(w, v, index - 1, c - w[index]));
return memo[index][c] = res;
}
public static void main(String[] args) {
InputStream is = ZeroOnePack.class.getClassLoader().getResourceAsStream("bag/zero/ZeroOnePack.txt");
Scanner scanner = new Scanner(is);
int N = scanner.nextInt();//物品个数【也可以看做是物品种类数目,在01背包问题中一种物品只有一件】
int C = scanner.nextInt();//背包容量
int[] w = new int[N ];//物品体积
int[] v = new int[N ];//物品价值
for (int k = 0; k < N; k++) {
w[k] = scanner.nextInt();
v[k] = scanner.nextInt();
}
System.out.print(N + "\t");
System.out.println(C);
for (int k = 0; k < N; k++) {
System.out.print(w[k] + "\t");
System.out.println(v[k]);
}
int res = new Solution1().knapsack01(w, v, C);
System.out.println(res);
}
}结果
3 10
3 4
4 5
5 6
11
自底向上的求解
优化:动态规划
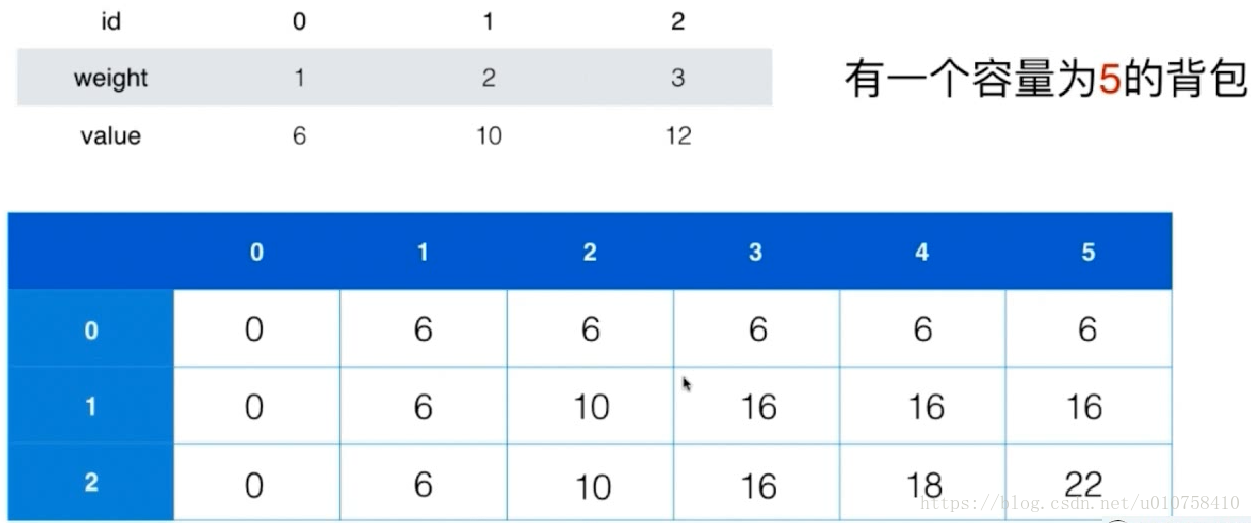
举个栗子看看整个过程:状态中涉及到两个变量,我们使用两个参数来定义状态,自然记忆化空间就是二维数组了。
int knapsack01(const vector<int> &w, const vector<int> &v, int W){
assert( w.size() == v.size() );
int n = w.size();
vector<vector<int>> memo( n, vector<int>(W+1,0));
//解决基础问题:0号物品一次放入容量为[0...C]的背包
for( int j = 0 ; j <= W ; j ++ )
memo[0][j] = ( j >= w[0] ? v[0] : 0 );
//依次将后续编号物品放入容量为[0-C]的背包
//后续放入操作是在之前放入操作基础上进行的
for( int i = 1 ; i < n ; i ++ )
for( int j = 0 ; j <= W ; j ++ ){
//第i件物品:不放
memo[i][j] = memo[i-1][j];
if( j >= w[i] )
//第i将物品:放入
memo[i][j] = max( memo[i][j], v[i] + memo[i-1][j-w[i]]);
}
//此时全部物品放入容量的C的背包
return memo[n-1][W];
}
放出大牛的代码:
https://github.com/liuyubobobo/Play-with-Algorithm-Interview/blob/master/09-Dynamic-Programming/Course%20Code%20(C%2B%2B)/05-0-1-knapsack/main2.cpp
算法复杂度:
时间复杂度:O(n*C)
空间复杂度:O(n*C)
思考还能优化吗?其实我们可以优化空间复杂度
01背包的优化
空间O(n*C)->O(2*C)

从空间复杂度进行优化。参考如上的代码和图片以及我们的状态转移方程,我们发现,每次都是对一行中的元素进行更新,而更新该行元素是值参考到了他的上一行元素,在之前的元素均可看做无用信息,是可以丢弃了。话句话来讲,我们只要知道了一行元素,就可以求出它的下一行元素,而之前行的元素已经没有用了。
int knapsack01(const vector<int> &w, const vector<int> &v, int W){
assert( w.size() == v.size() );
int n = w.size();
vector<vector<int>> memo( 2, vector<int>(W+1,0));
for( int j = 0 ; j <= W ; j ++ )
memo[0][j] = ( j >= w[0] ? v[0] : 0 );
for( int i = 1 ; i < n ; i ++ )
for( int j = 0 ; j <= W ; j ++ ){
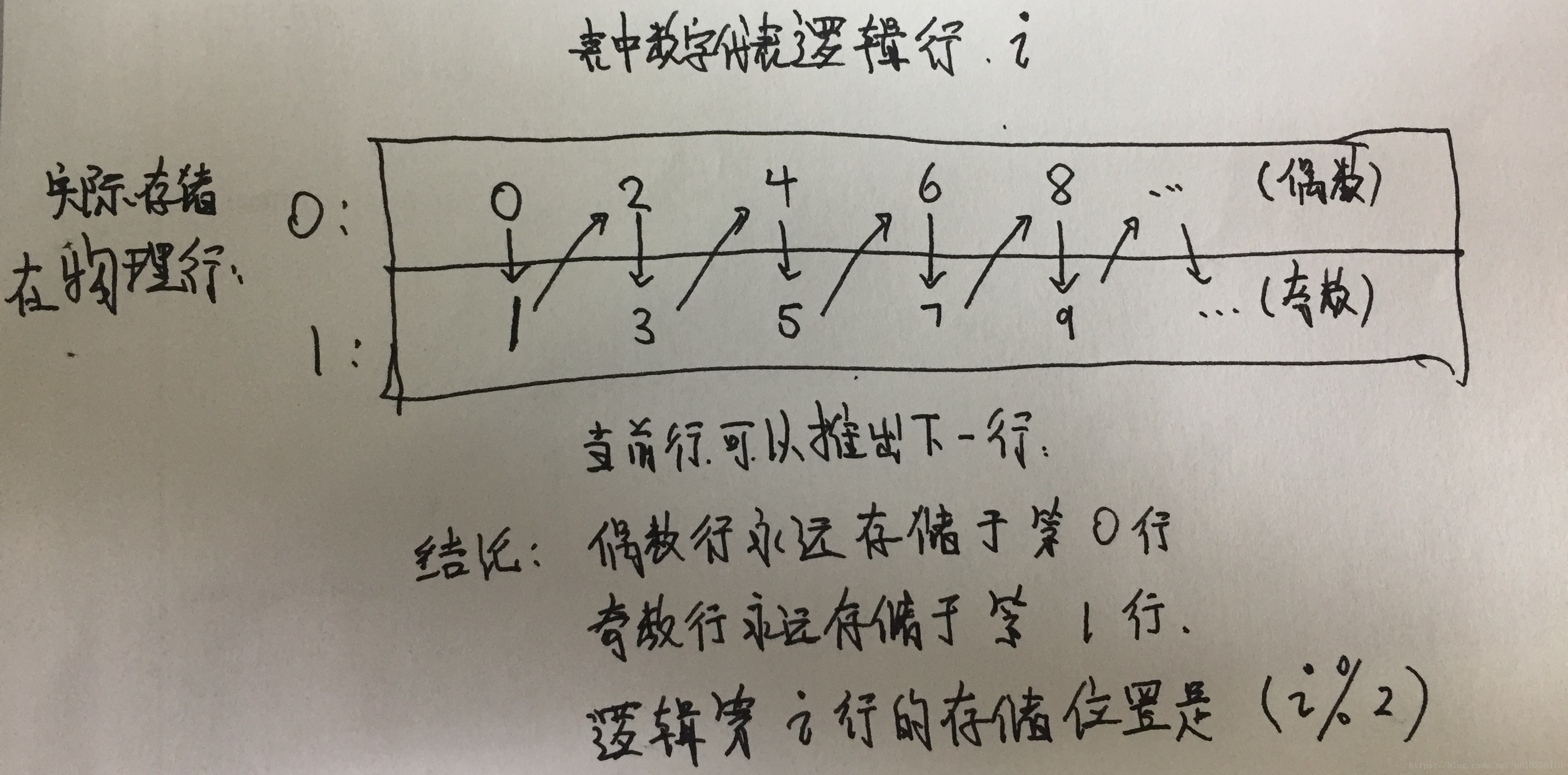
//当前逻辑行i的实际存储位置[i%2]
//上一逻辑行i-1的实际存储位置[(i-1)%2]
memo[i%2][j] = memo[(i-1)%2][j];
if( j >= w[i] )
memo[i%2][j] = max( memo[i%2][j], v[i] + memo[(i-1)%2][j-w[i]]);
}
return memo[(n-1)%2][W];
}我们来思考能不能做的更好呢?
空间O(2*C)->O(C)
思考:能不能只用一行来完成数据的更新
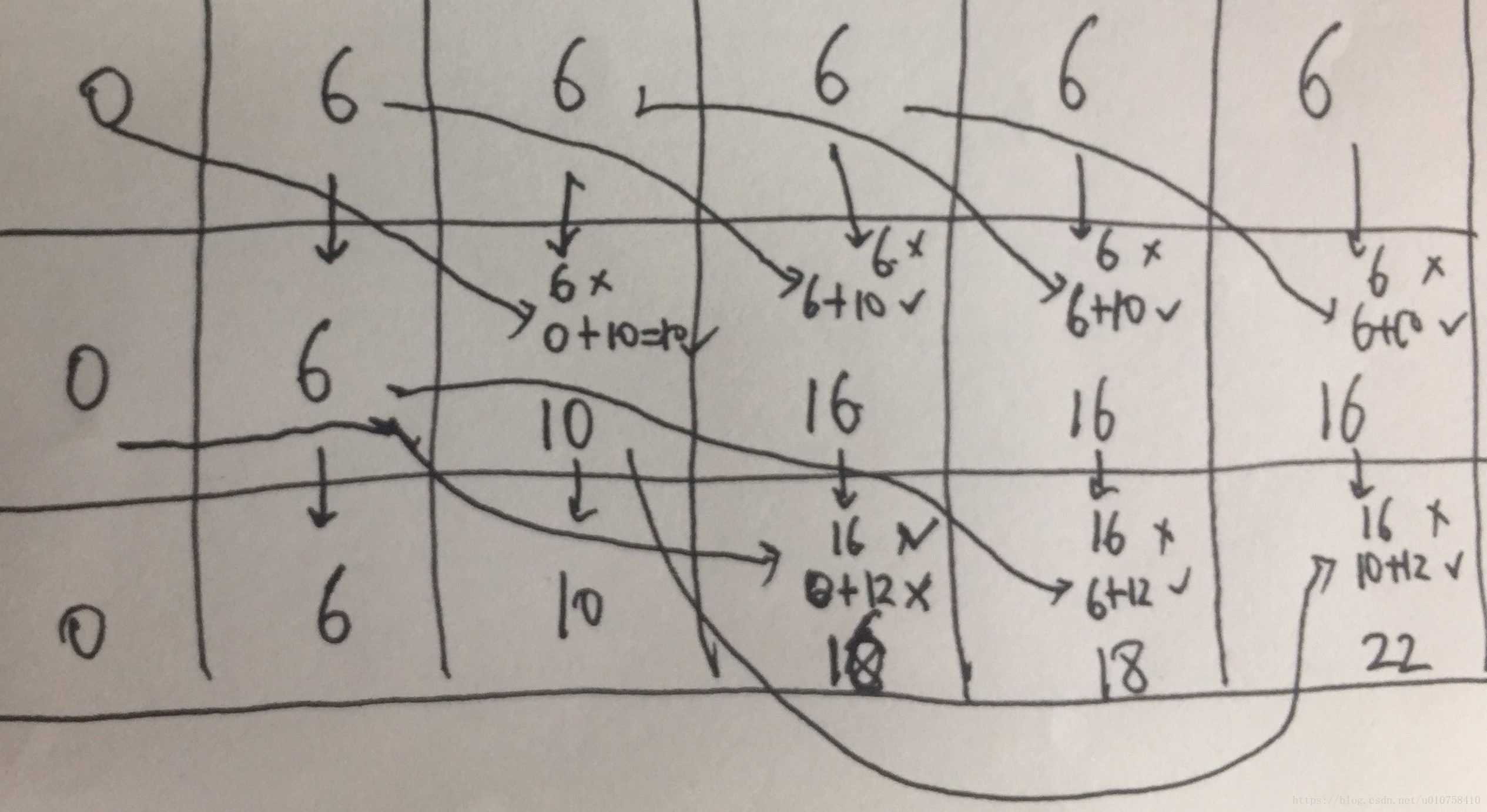
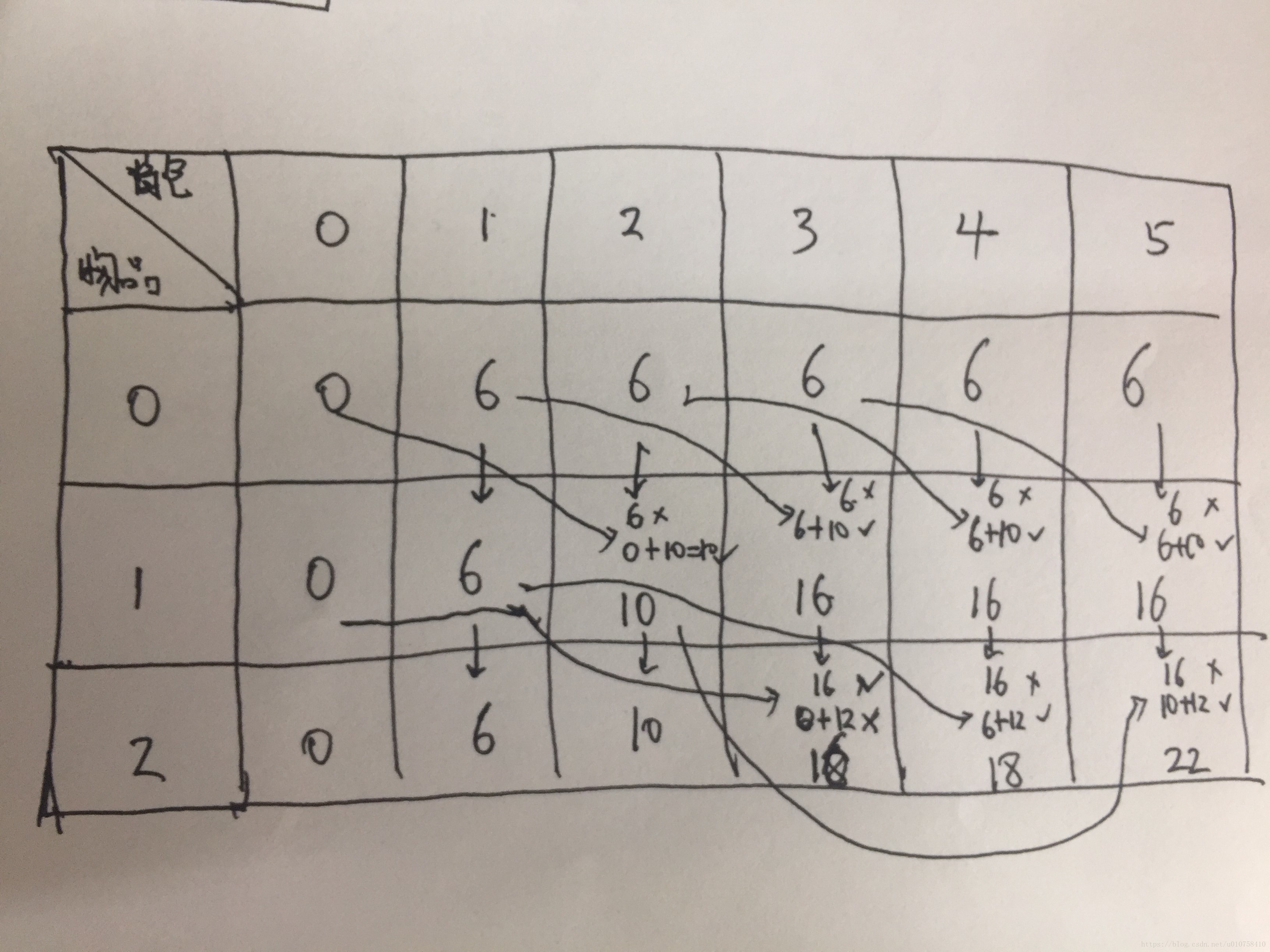
上图表示利用上一行数据来求解当前行数据的过程。通过观察箭头的方向,我们会发现,求解当前行中的元素时,会对比上一行的同样位置的元素(图中竖直箭头)和上一行中左侧的某个元素(图中斜线箭头)。
我们尝试用一行数据来完成问题的求解:在手动初始化第0行数据之后(基础数据),递推求解之后行数据的时候,我们通过倒序索引的方式,来填充数据。
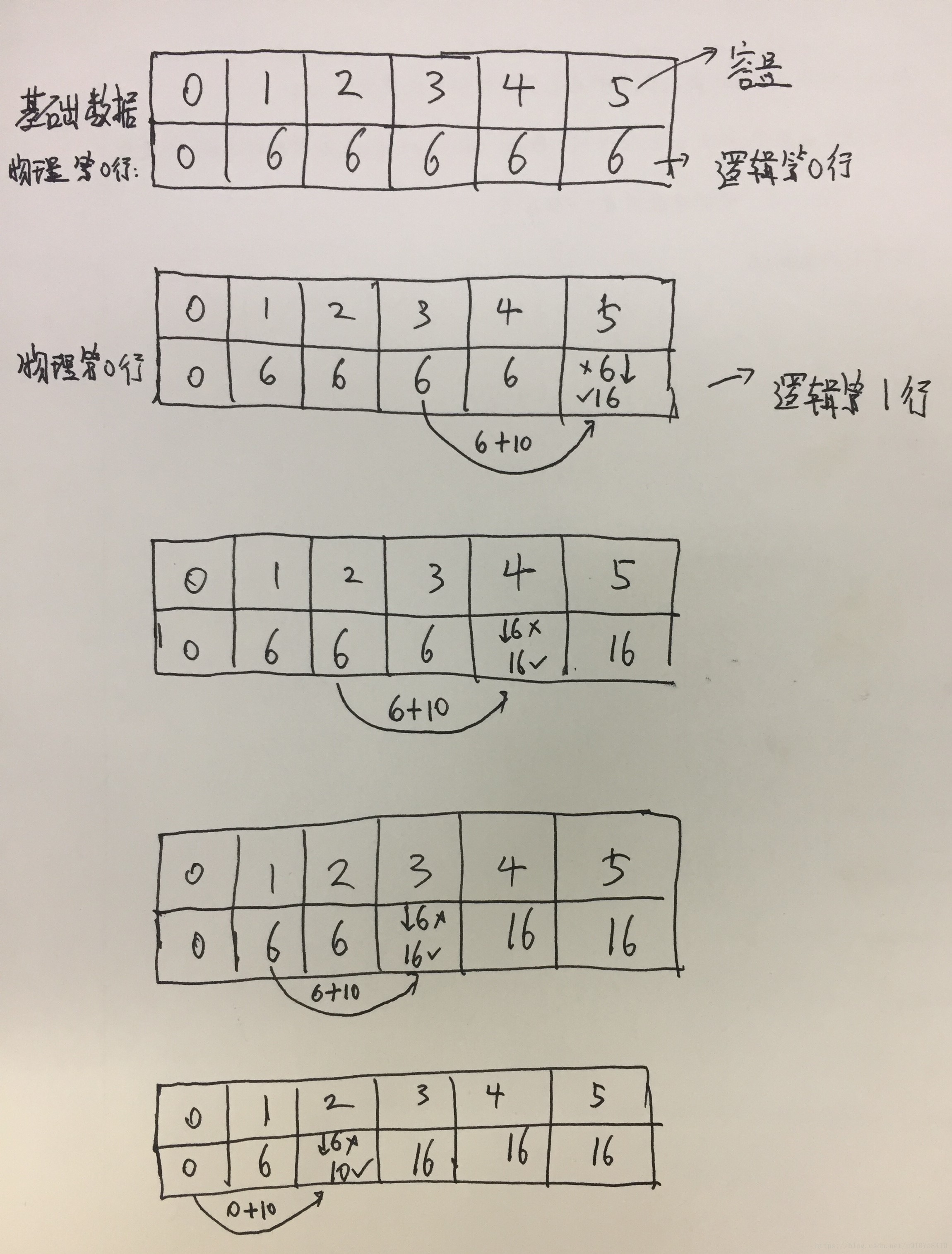
为什么要用倒序索引呢?在填充下一行的某个元素时,会参考上一行的相同位置的元素和上一行该位置之前的某个元素。那么在倒序索引填充数据的时候,要参考的上一行的相同位置的元素就是当前元素,要参考的上一行该位置之前的某个元素就是当前元素左侧的某个元素。这样通过倒叙填充数据的方式,就可以在一行数据空间中完成问题的求解。
举个例子,从第0行求解第1行的过程。
int knapsack01(const vector<int> &w, const vector<int> &v, int W){
assert( w.size() == v.size() );
int n = w.size();
vector<int> memo(W+1,0);
//基础数据(底)填充第0行数据
for( int j = 0 ; j <= W ; j ++ )
memo[j] = ( j >= w[0] ? v[0] : 0 );
//倒叙填充0行之后的所有数据
for( int i = 1 ; i < n ; i ++ )
for( int j = W ; j >= w[i] ; j -- )
//与逻辑上一行相同位置比较;与逻辑上一行之前的位置相比较
memo[j] = max( memo[j], v[i] + memo[j-w[i]]);
return memo[W];
}01背包问题的变种
完全背包问题:
完全背包问题:每个物品可以无限使用。
其实背包容量是有限的,每个物品能放置的个数是都有一个最大值的,这就将无限物品使用的背包问题转化成了有限物品使用的背包问题,只不过我们选取的物品列表中会有重复出现的物品而已。
看一个例子:

也可以用01背包的优化思路进行求解可以进行优化:(看箭头方向还是上一行同一位置,和至少一个位于上一行该位置之前的一些元素)仍然是采用倒叙填充数据,
import java.io.InputStream;
import java.util.Arrays;
import java.util.Scanner;
public class MyCompletePack {
public static int getCompletePack(int[] w, int[] v, int C) {
int n = w.length;
int[] memo = new int[C + 1];
Arrays.fill(memo, 0);
//基础数据,填充第0行,用第一种物品填充背包
for (int j = 0; j < C + 1; j++) {
//k = j / w[0]
memo[j] = ((j / w[0]) > 0 ? v[0] * (j / w[0]) : 0);
System.out.print(memo[j] + "\t");
}
System.out.println();
//递推第i中物品的存放方案
for (int i = 1; i < n; i++) {
//仍然是倒叙填充,k = j / w[i]
for (int j = C; j >= w[i]; j--) {
memo[j] = Math.max(memo[j], memo[j - (j / w[i]) * w[i]] + (j / w[i]) * v[i]);
}
// 输出第i行数据
for (int j = 0; j < C + 1; j++) {
System.out.print(memo[j] + "\t");
}
System.out.println();
}
return memo[C];
}
public static void main(String[] args) {
int maxValue = 0;
InputStream is = CompletePack.class.getClassLoader().getResourceAsStream("bag/complete/CompletePack.txt");
Scanner scanner = new Scanner(is);
int N = scanner.nextInt();//物品种类数目
int C = scanner.nextInt();//背包容量
int[] w = new int[N];//物品体积,默认初始化为0,为了方便理解角标从1开始
int[] v = new int[N];//物品价值
for (int k = 0; k < N; k++) {
w[k] = scanner.nextInt();
v[k] = scanner.nextInt();
}
int res = getCompletePack(w, v, C);
System.out.println("maxValue = " + res);
}
}
输出结果与我们的图解一致
0 2 4 6 8 10
0 2 5 7 10 12
0 2 5 9 11 14
maxValue = 14多重背包:
多重背包:每个物品不止一个,有num(i)个
介于01和完全背包之间。
状态定义:f (n, c):表示将n种物品放入容量为c的背包,所能达到的最大值。
状态转移方程:f (i, c) = max { k * v [i] + f (i-1, c - k * w [i]) | 0<= k <=n[i] }
多重背包与完全背包的区别:二者均可以转换成0-1背包来求解,不同的是,在0-1背包中,每种物品只有一件;而在完全背包问题中,每种物品的个数的无限的想放多少放多少;在多重背包中,每种物品的个数是有限的不得超过 n [ i ] 件。
在完全背包问题中,当背包的容量为 j 的时候,此时的背包中一定可以放置j / w [ i ] 件物品(因为每种物品是无限提供的)。而在多重背包问题中,当背包的容量为 j 的时候,此时的背包中不一定能放 j / w[ i ] 件物品(因为每种物品有数量限制 n [ i ]),这样实际放置的物品的件数为: min ( j / w [ i ],n [ i ] )
import java.io.InputStream;
import java.util.Arrays;
import java.util.Scanner;
public class MyMultiplePack {
public static int getMultiplePack(int[] w, int[] v, int[] n, int C) {
int N = w.length;
int[] memo = new int[C + 1];
Arrays.fill(memo, 0);
//基础数据,填充第0行,用第一种物品填充背包
for (int j = 0; j < C + 1; j++) {
//在不超过第0种物品个数限制和背包体积限制的情况下,可以达到的最大价值。
//(j / w[0])为最多可以容纳第0种物品的个数,n[0]为第0中物体实际有多少个。
memo[j] = ((j / w[0]) > 0 ? Math.min((j / w[0]), n[0]) * v[0] : 0);
System.out.print(memo[j] + "\t");
}
System.out.println();
//递推第i中物品的存放方案
for (int i = 1; i < N; i++) {
for (int j = C; j >= w[i]; j--) {
// 第i中物品有数量限制,我们这里比较实际数目和背包里最多能放下的数目,去取最小值。
memo[j] = Math.max(memo[j], memo[j - Math.min((j / w[i]), n[i]) * w[i]] + Math.min((j / w[i]), n[i]) * v[i]);
}
// 输出第i行数据
for (int j = 0; j < C + 1; j++) {
System.out.print(memo[j] + "\t");
}
System.out.println();
}
return memo[C];
}
public static void main(String[] args) {
int maxValue = 0;
InputStream is = CompletePack.class.getClassLoader().getResourceAsStream("bag/multiple/MultiplePack2.txt");
Scanner scanner = new Scanner(is);
int N = scanner.nextInt();//物品种类数目
int C = scanner.nextInt();//背包容量
int[] w = new int[N];//物品体积
int[] v = new int[N];//物品价值
int[] n = new int[N];//每种物品的数目
for (int k = 0; k < N; k++) {
w[k] = scanner.nextInt();
v[k] = scanner.nextInt();
n[k] = scanner.nextInt();
}
int res = getMultiplePack(w, v, n, C);
System.out.println("maxValue = " + res);
}
}
数据和结果
3(N) 5(C)
1(w) 2(v) 3(n)
2 5 2
3 9 0
----------------------
0 2 4 6 6 6
0 2 5 7 10 12
0 2 5 7 10 12
maxValue = 12多维费用背包问题:
多维费用背包问题:要考虑物品的体积和重量两个维度,背包同时又体积可承重的约束
物品之间加入更多的约束,
物品之间加入更多的约束:比如物品之间可以相互排斥;也可以相互依赖。
背包的练习题
有时候我们遇到的问题表面上看来不是一个背包问题,但是经过分析之后,其实仍然是背包问题。
【416】Partition Equal Subset Sum
给定一个非空数组,其中所有的数字都是正整数。问是否可以将这个数组的元素分成两部分,使得每部分的数字和相等?
如对【1,5,11,5】,可以分成【1,5,5】和【11】两部分,元素和相等,返回true。
如对【1,2,3,5】,无法分成元素和相等的两部分,返回false。
分析:
典型的背包问题,在n个物品中选出一定物品,填满sum/2的背包
状态:F( n,C) 考虑将n个物品填满容量为C的背包
状态转移方程:F ( i,c) = F( i-1,c) II F( i-1,c-w(i) )
时间复杂度:O(n*sum/2)=O(n*sum)
#include <iostream>
#include <vector>
#include <cassert>
using namespace std;
/// 416. Partition Equal Subset Sum
/// https://leetcode.com/problems/partition-equal-subset-sum/description/
/// 记忆化搜索
/// 时间复杂度: O(len(nums) * O(sum(nums)))
/// 空间复杂度: O(len(nums) * O(sum(nums)))
class Solution {
private:
// memo[i][c] 表示使用索引为[0...i]的这些元素,是否可以完全填充一个容量为c的背包
// -1 表示为未计算; 0 表示不可以填充; 1 表示可以填充
vector<vector<int>> memo;
// 使用nums[0...index], 是否可以完全填充一个容量为sum的背包
bool tryPartition(const vector<int> &nums, int index, int sum){
//背包填满
if(sum == 0)
return true;
//无法填满背包
//超出背包容量,或物品不够背包仍有剩余空间
if(sum < 0 || index < 0)
return false;
if(memo[index][sum] != -1)
return memo[index][sum] == 1;
memo[index][sum] = (tryPartition(nums, index - 1, sum) ||
tryPartition(nums, index - 1, sum - nums[index])) ? 1 : 0;
return memo[index][sum] == 1;
}
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for(int i = 0 ; i < nums.size() ; i ++){
assert(nums[i] > 0);
sum += nums[i];
}
if(sum % 2)
return false;
memo.clear();
for(int i = 0 ; i < nums.size() ; i ++)
memo.push_back(vector<int>(sum / 2 + 1, -1));
return tryPartition(nums, nums.size() - 1, sum / 2);
}
};
int main() {
int nums1[] = {1, 5, 11, 5};
vector<int> vec1(nums1, nums1 + sizeof(nums1)/sizeof(int));
if(Solution().canPartition(vec1))
cout << "true" << endl;
else
cout << "false" << endl;
int nums2[] = {1, 2, 3, 5};
vector<int> vec2(nums2, nums2 + sizeof(nums2)/sizeof(int));
if(Solution().canPartition(vec2))
cout << "true" << endl;
else
cout << "false" << endl;
return 0;
}#include <iostream>
#include <vector>
using namespace std;
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for( int i = 0 ; i < nums.size() ; i ++ )
sum += nums[i];
if( sum%2 )
return false;
int n = nums.size();
int W = sum/2;
vector<bool> memo(W+1,false);
//初始化:看第0件物品能不能将背包填满【自底向上的基础数据】
for( int i = 0 ; i <= W ; i ++ )
memo[i] = ( nums[0] == i );
//计算之后的物品能不能将背包填满【递推数据】
for( int i = 1 ; i < n ; i ++ )
//倒叙填充(优化手段)
for( int j = W ; j >= nums[i] ; j -- )
//已经满了,无需放入该物品,或者放入该物品之后恰好填满背包
memo[j] = memo[j] || memo[j-nums[i]];
return memo[W];
}
};
int main() {
int nums1[] = {1, 5, 11, 5};
vector<int> vec1(nums1, nums1 + sizeof(nums1)/sizeof(int));
if( Solution().canPartition(vec1) )
cout<<"true"<<endl;
else
cout<<"false"<<endl;
int nums2[] = {1, 2, 3, 5};
vector<int> vec2(nums2, nums2 + sizeof(nums2)/sizeof(int));
if( Solution().canPartition(vec2) )
cout<<"true"<<endl;
else
cout<<"false"<<endl;
return 0;
}【322】Coin Change

【377】Combination Sum 4

【474】Ones and Zeroes

【139】Word Break

【494】Target Sum
LIS
最长上升子序列
【300】Longest Increasing Subsequence

状态定义和状态转移方程

图像演示
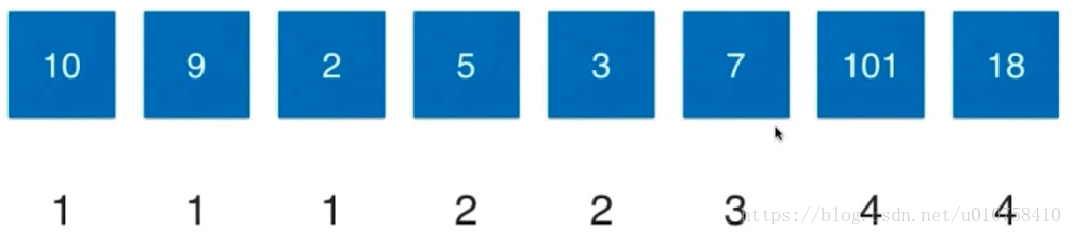
记忆化搜索示例代码:
https://github.com/liuyubobobo/Play-with-Algorithm-Interview/blob/master/09-Dynamic-Programming/Course%20Code%20(C%2B%2B)/08-Longest-Increasing-Subsequence/main.cpp
动态规划示例代码:
https://github.com/liuyubobobo/Play-with-Algorithm-Interview/blob/master/09-Dynamic-Programming/Course%20Code%20(C%2B%2B)/08-Longest-Increasing-Subsequence/main2.cpp
练习题【376】Wiggle Subsequence
LCS
Longest Common Sequence 最长公共子序列

状态和状态转移方程

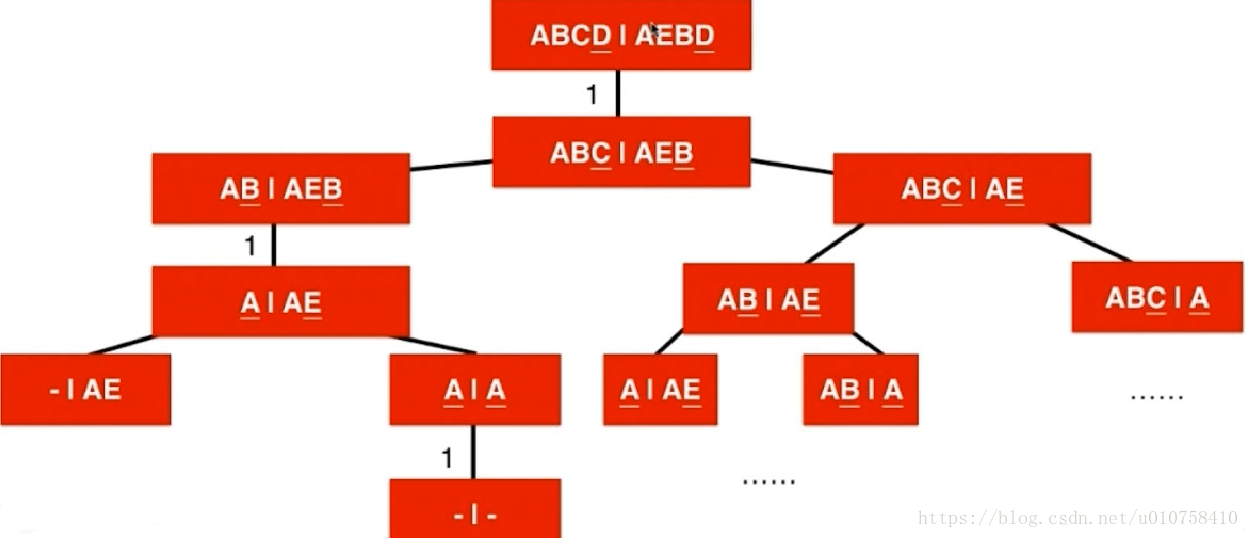
递归树
最短路径
dijkstra单源最短路径算法也是动态规划

























 2333
2333











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








