在应用机器学习算法时,我们通常采用梯度下降法来对采用的算法进行训练。其实,常用的梯度下降法还具体包含有三种不同的形式,它们也各自有着不同的优缺点。
下面我们以线性回归算法来对三种梯度下降法进行比较。
一般线性回归函数的假设函数为:
hθ=∑nj=0θjxj
对应的能量函数(损失函数)形式为:
Jtrain(θ)=1/(2m)∑mi=1(hθ(x(i))−y(i))2
下图为一个二维参数( θ0 和 θ1 )组对应能量函数的可视化图:

1. 批量梯度下降法BGD
批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新,其数学形式如下:
(1) 对上述的能量函数求偏导:
(2) 由于是最小化风险函数,所以按照每个参数 θ 的梯度负方向来更新每个 θ :
具体的伪代码形式为:
repeat{
(for every j=0, ... , n)
}
从上面公式可以注意到,它得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果样本数目 m 很大,那么可想而知这种方法的迭代速度!所以,这就引入了另外一种方法,随机梯度下降。
从迭代的次数上来看,BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下:

2. 随机梯度下降法SGD
由于批量梯度下降法在更新每一个参数时,都需要所有的训练样本,所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法(Stochastic Gradient Descent,简称SGD)正是为了解决批量梯度下降法这一弊端而提出的。
将上面的能量函数写为如下形式:
利用每个样本的损失函数对 θ 求偏导得到对应的梯度,来更新 θ :
具体的伪代码形式为:
1. Randomly shuffle dataset;
2. repeat{
for i=1, ... , m {
(for j=0, ... , n )
}
}
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
从迭代的次数上来看,SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下:

3. 小批量梯度下降法MBGD
有上述的两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即,算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。
MBGD在每次更新参数时使用b个样本(b一般为10),其具体的伪代码形式为:
Say b=10, m=1000.
Repeat{
for i=1, 11, 21, 31, ... , 991{

(for every j=0, ... , n )
}
}
梯度下降法的缺点是:
- 靠近极小值时速度减慢。
- 直线搜索可能会产生一些问题。
- 可能会'之字型'地下降。
由于梯度下降法收敛速度慢,而随机梯度下降法会快很多
–根据某个单独样例的误差增量计算权值更新,得到近似的梯度下降搜索(随机取一个样例)
–可以看作为每个单独的训练样例定义不同的误差函数
–在迭代所有训练样例时,这些权值更新的序列给出了对于原来误差函数的梯度下降的一个合理近似
–通过使下降速率的值足够小,可以使随机梯度下降以任意程度接近于真实梯度下降
•标准梯度下降和随机梯度下降之间的关键区别
–标准梯度下降是在权值更新前对所有样例汇总误差,而随机梯度下降的权值是通过考查某个训练样例来更新的
–在标准梯度下降中,权值更新的每一步对多个样例求和,需要更多的计算
–标准梯度下降,由于使用真正的梯度,标准梯度下降对于每一次权值更新经常使用比随机梯度下降大的步长
–如果标准误差曲面有多个局部极小值,随机梯度下降有时可能避免陷入这些局部极小值中








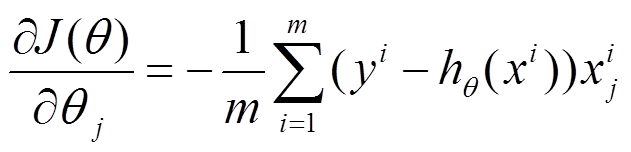
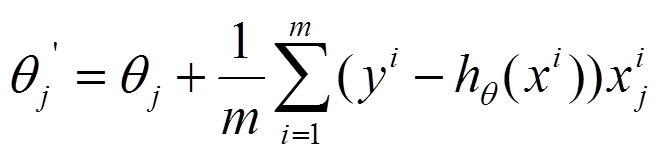
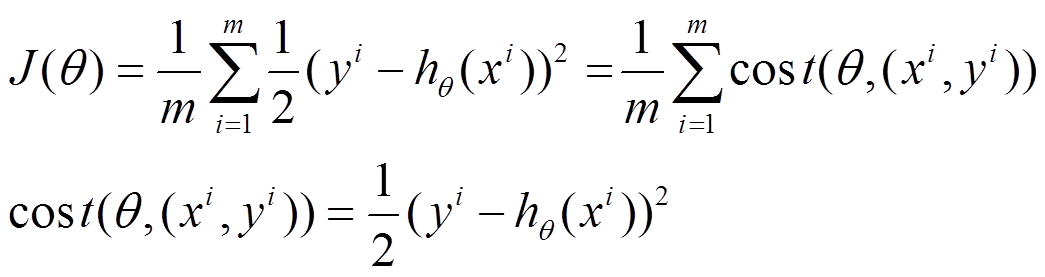














 416
416

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








