隐马尔可夫模型学习笔记（二）

前言
前文所述，要理解隐马尔可夫首先需要梳理几个步骤：

1. 如何理解概念

2. 什么叫转移概率矩阵和生成概率矩阵

3. 模型公式

5. 公式的求解过程

6. python代码串接

五、公式的求解过程

上一篇中，我们提到HMM可以解决的三个经典问题，我们现在就看下问题一
评估可观测序列概率。即给定模型$\lambda =(A,B,\eta )$和观测序列$O=o_1,o_2,...o_T$，计算在模型𝜆下可观测序列𝑂出现的概率𝑃(𝑂|𝜆)， 如上述例子的骰子，如投3次，可观测的点数序列1，6，3 的概率是多少？

5.1 例举法

求上述问题的时，我们可以暴力求解，如下

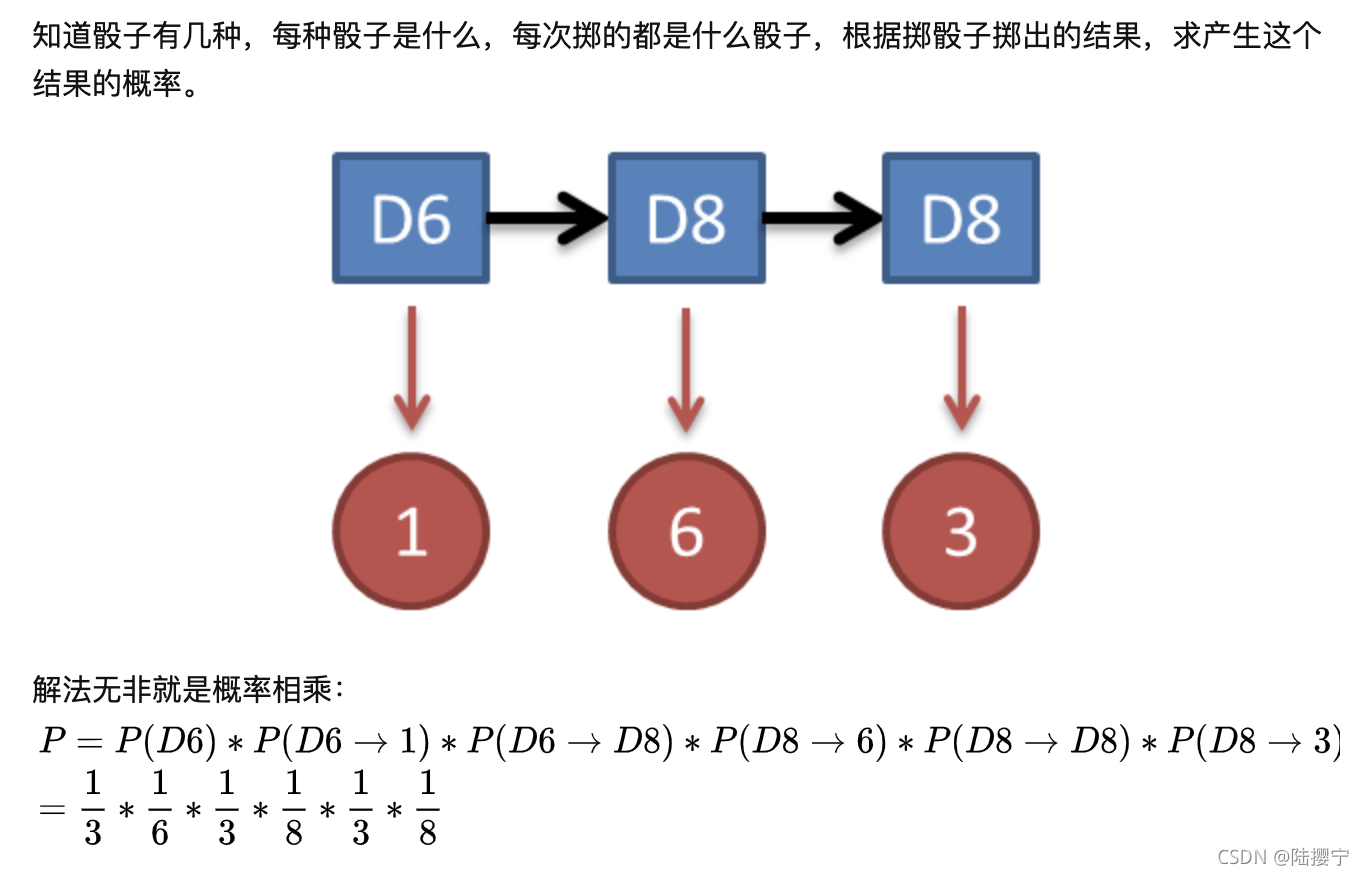
上图只是我们在例句当骰子的不可观测序列为D6->D8->D8的情况，还有其他的不可观测序列，就不一一列出来了，下面是用公式的形式展示出来。
我们可以列举出所有可能出现的长度为𝑇的不可观测序列$I=i_1,i_2,...,i_T$,分布求出这些不可观测序列与可观测序列$O=o_1,o_2,...o_T$的联合概率分布𝑃(𝑂,𝐼|𝜆)，这样我们就可以很容易的求出边缘分布𝑃(𝑂|𝜆)了，公式如下：

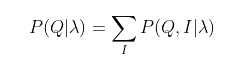
其中， 联合分布可以拆分成下面个式子：

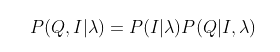
其中， 由于任意一个不可观测序列$I=i_1,i_2,...,i_T$出现的概率是：

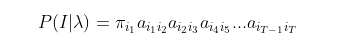
然后，我们先固定一个不可观测序列$I=i_1,i_2,...,i_T$下，求可观测序列$O=o_1,o_2,...o_T$出现的概率：

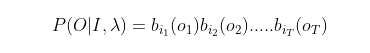
所以，综上所述，我们得到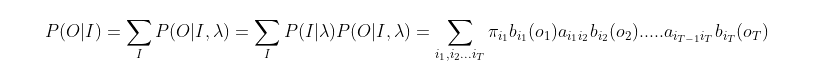
上面公式就是我们把所有的组合都相乘起来，那么可观测状态就有$N^T$种组合方式，我们得到的算法的时间复杂度是$O(T{N}^T)$阶的。对于一些不可观测状态数极少的模型，我们可以用这种求解法来得到观测序列出现的概率，但是如果不可观测状态多，则上述算法太耗时了，所以我们还需要找到另一种方法解题。

5.2 前向后向算法

前向后向算法是前向算法和后向算法的统称，这两个算法都可以用来求HMM观测序列的概率

5.2.1 前向算法

概念：前向算法本质上属于动态规划的算法，也就是我们要通过找到局部状态递推的公式，这样一步步的从子问题的最优解拓展到整个问题的最优解。

那么在前向算法中，通过定义“前向概率”来定义动态规划的这个局部状态（时刻t之前）。什么是前向概率呢, 其实定义很简单：定义时刻 𝑡 时不可观测状态为$q_k,k\in N$, 观测状态的序列为$O_t=o_1,o_2,...o_t$的概率为前向概率。记为：

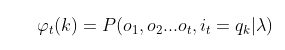
既然是动态规划，我们就要递推了，现在我们假设我们已经找到了在时刻𝑡时各个不可观测状态的前向概率（也就是说上面公式只表达了不可观测状态为$q_k$的前向概率），现在我们需要递推出时刻𝑡+1时各个不可观测状态的前向概率。

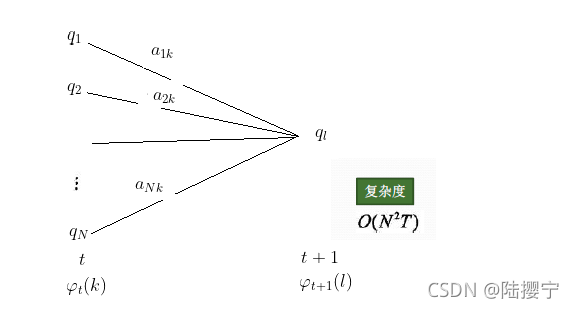
上图
1）我们可以基于时刻𝑡时各个(N个)不可观测状态的前向概率${\phi }_t(k)$，再乘以对应的不可观测的状态转移概率$a_{kl}$，即:

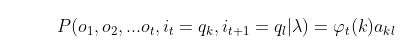
就是在时刻 𝑡 可观测到$O_t=o_1,o_2,...o_t$，其中$i_t=q_k,k\in N$；$i_{t+1}=q_l,l\in N$ 的概率,（只把时刻t的不可观测的$q_k$都考虑了）

2）如果想将下面所有的线对应的概率求和，即:

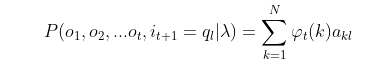
就是在时刻𝑡可观测到$O_t=o_1,o_2,...o_t$，其中$i_{t+1}=q_l,l\in N$ 的概率，（都把时刻t的各个不可观测的$q_N$都考虑了）

3）继续一步，由于可观测状态$o_{t+1}$只依赖于𝑡+1时刻不可观测状态$q_l$, 这样

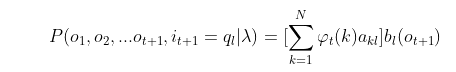
就是在在时刻𝑡+1可观测到$O_{t+1}=o_1,o_2,...o_{t+1}$，其中$i_{t+1}=q_l$

而这个概率，恰恰就是时刻𝑡+1对应的不可观测状态$l$的前向概率（看上面定义前向概率的公式），这样我们得到了前向概率的递推关系式如下：

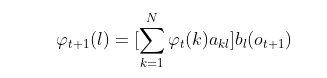
我们的动态规划从时刻1开始，到时刻𝑇结束，由于${\phi }_T(K)$表示在时刻𝑇观测序列为$O_T=o_1,o_2,...o_T$，并且时刻𝑇不可观测状态$q_K$的概率，我们只要将所有不可观测状态对应的概率相加，即:

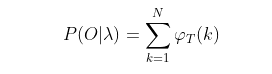
就得到了在时刻𝑇观测序列为$O_T=o_1,o_2,...o_T$的概率。

下面总结下前向算法。

输入： HMM模型𝜆=(𝐴,𝐵,Π)，观测序列$O_T=(o_1,o_2,...o_T)$
输出： 观测序列概率𝑃(𝑂|𝜆)

1. 计算时刻1的各个隐藏状态前向概率：
   
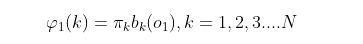
2. 递推时刻2,3,…𝑇时刻的前向概率：
   
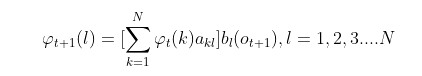
3. 计算最终结果：
   
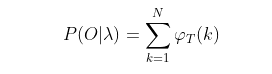
   从递推公式可以看出，我们的算法时间复杂度是𝑂(𝑇𝑁2)，比暴力解法的时间复杂度𝑂(𝑇𝑁𝑇)少了几个数量级。
   (有个实际例子请看参考资料3. HMM前向算法求解实例)

5.2.1 后向算法

后向算法和前向算法非常类似，都是用的动态规划，唯一的区别是选择的局部状态不同，后向算法用的是“后向概率”，那么后向概率是如何定义的？ 定义时刻t时不可观测状态为$q_k$, 从时刻t+1到最后时刻T的观测状态的序列为$o_{t+1},o_{t+2},...o_T$的概率为后向概率。记为：

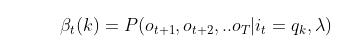
后向概率的动态规划递推公式和前向概率是相反的。现在我们假设我们已经找到了在时刻t+1时各个不可观测状态的后向概率${\beta }_{t+1}(l)$，现在我们需要递推出时刻t时各个不可观测状态的后向概率。

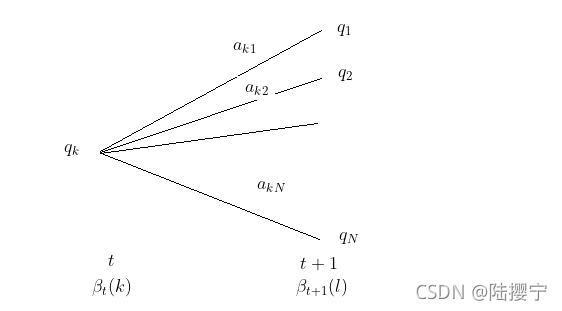
上图
1）我们可以计算出观测状态的序列为$o_{t+2},o_{t+3},...o_T$， t时隐藏状态为$q_k$, 时刻t+1隐藏状态为$q_l$的概率:

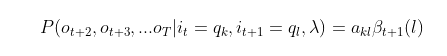
2）接着可以得到观测状态的序列为$o_{t+1},o_{t+2},...o_T$， t时隐藏状态为$q_k$, 时刻t+1隐藏状态为$q_l$的概率:

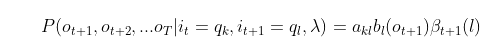
3）把下面所有线对应的概率加起来，我们可以得到观测状态的序列为$o_{t+1},o_{t+2},...o_T$， t时隐藏状态为$q_k$的概率为

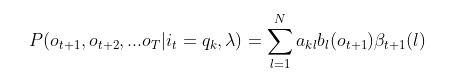
这个概率即为时刻t的后向概率　，这样我们得到了后向概率的递推关系式如下：

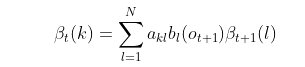
现在我们总结下后向算法的流程,注意下和前向算法的相同点和不同点：

输入： HMM模型λ=(A,B,Π)，观测序列O=(o1,o2,…oT)
输出： 观测序列概率P(O|λ)

1. 初始化时刻T的各个隐藏状态后向概率：
   
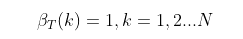
2. 递推时刻T−1,T−2,…1时刻的后向概率：
   
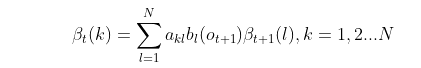
3. 计算最终结果：
   

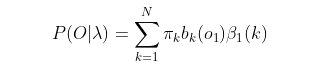
此时我们的算法时间复杂度仍然是O(TN2)。