【noip】【lca】火车运输 倍增

这几天把13年的提高做了，最后两道题参考了网上许多代码，最后终于改出来了，这里是day1最后一题。

描述

A 国有 n 座城市，编号从 1 到 n，城市之间有 m 条双向道路。每一条道路对车辆都有重量限制，简称限重。现在有 q 辆货车在运输货物，司机们想知道每辆车在不超过车辆限重的情况下，最多能运多重的货物。

输入格式

第一行有两个用一个空格隔开的整数 n，m，表示 A 国有 n 座城市和 m 条道路。
接下来 m 行每行 3 个整数 x、y、z，每两个整数之间用一个空格隔开，表示从 x 号城市到 y 号城市有一条限重为 z 的道路。注意：x 不等于 y，两座城市之间可能有多条道路。
接下来一行有一个整数 q，表示有 q 辆货车需要运货。
接下来 q 行，每行两个整数 x、y，之间用一个空格隔开，表示一辆货车需要从 x 城市运输货物到 y 城市，注意：x 不等于 y。

输出格式

输出共有 q 行，每行一个整数，表示对于每一辆货车，它的最大载重是多少。如果货车不能到达目的地，输出-1。

样例

输入

4 3
1 2 4
2 3 3
3 1 1
3
1 3
1 4
1 3

输出

3
-1
3

限制

每个测试点1s。
提示
对于 30%的数据，0 < n < 1,000，0 < m < 10,000，0 < q < 1,000；
对于 60%的数据，0 < n < 1,000，0 < m < 50,000，0 < q < 1,000；
对于 100%的数据，0 < n < 10,000，0 < m < 50,000，0 < q < 30,000，0 ≤ z ≤ 100,000。

来源

NOIP 2013 提高组 Day 1

---

先是不知道怎么做，spfa乱搞，dijikstra乱搞，用floyed写了个对拍，对出来没问题，结果交上去T了 85%。。。
下来看了一下，先了求最大生成树，再spfa乱搞，又交上去，只T了40%。
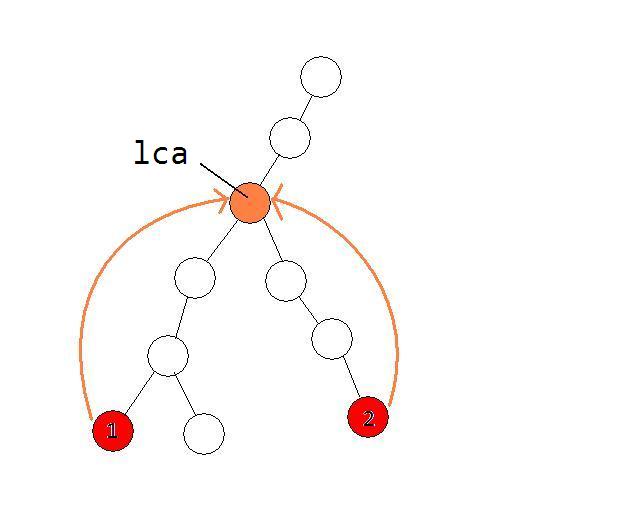
后来看了某位大大的倍增求lca（最近公共祖先）

---

有了lca，做出来就很轻松了，我们只需要先跑一边kruskal，把最大生成树求出来，然后求出1点到 lca 的最小值，再求出 2到 lca的最小值，然后再取一个最小值就出来了。

那么，现在 问题就来了

1、如何建树

2、如何找lca

3、如何找最小值

---

一、如何建树

kruskal跑一边，把最大生成树需要使用的边mark，但一定要注意，不能和直接使用最大生成树，因为跑的时候我们用的是并查集，树早就长得和原来不一样了。
跑完kruskal再跑一边dfs就可以把树建出来，同时把每个节点的深度求出来，但同时需要主要，每个节点还需保存它的根节点，因为可能不只存在一棵树

---

二、如何找lca

找lca是这里的核心问题，如果直接向上按着父节点跳就和spfa没什么区别了，复杂度没有优化，就要用倍增来找，一次向上跳2^i个节点，这样原来的O（n）就优化成O（log n)了
于是建立倍增数组fa[i][j],表示j这个节点向上的第2^i个是那里
同时很容易得出递推式fa[i][j]=fa[i-1][fa[i-1][j]]
fa[i][j]等于j向上移2^(i-1),再向上移2^(i-1)
于是：

void bz()//倍增 
{
    for(int i=1;i<=14;i++)
        for(int j=1;j<=n;j++)
            fa[i][j]=fa[i-1][fa[i-1][j]];       
}

建立完倍增数组判断就可以以log的速度进行了，先判断两个节点是否在一棵树，再将它们的深度上移成一样，在尽量同步上移但使两个节点不一样，这是两个节点就都在lca下面一个了，再上一一个就是lca了。

---

三、如何找最小值

最小值我们同样用倍增，用minax[i][j]（因为先跑了一个最大生成树，所以实际上是最小值的最大值，所以我叫它minax）表示表示j这个节点向上的2^i个这一段的最小值是什么，递推式一样，此处不再赘述

下面是我写的代码，仅提供参考

#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<vector>
#define N 10005
#define M 100005
#define INF 2147480000

using namespace std;

int n,m,q,t;
int fa[15][N],minax[15][N],depth[N],tfa[N],unuse[M],flag[N];

struct Edge
{
    int from,to,d;
}e[M];

vector<int> a[N];
bool com (const Edge &a,const Edge &b)
{
    return a.d>b.d;
}

int F(int x)//并查集 
{
    return x==tfa[x]?x:tfa[x]=F(tfa[x]);
}

void kruskal()
{
    for(int i=1;i<=n;i++)
        tfa[i]=i;
    for(int i=1;i<=2*m;i++)
    {
        int x=F(e[i].to),y=F(e[i].from);
        if(x!=y)
        {
            tfa[x]=y;
        }
        else unuse[i]=1;
    }
}


void dfs(int x)//找深度 建树 
{
    if(!a[x].empty())
        for(int i=0;i<a[x].size();i++)
        {
            int o=a[x][i];
            int t=e[o].to+e[o].from-x;
            if(!flag[t])
            {
                flag[t]=1;
                depth[t]=depth[x]+1;
                fa[0][t]=x;
                minax[0][t]=e[o].d;
                dfs(t);
            }

        }
}

void bz()//倍增 
{
    for(int i=1;i<=14;i++)
        for(int j=1;j<=n;j++)
        {
            fa[i][j]=fa[i-1][fa[i-1][j]];
            minax[i][j]=min(minax[i-1][j],minax[i-1][fa[i-1][j]]);
        }

}

int lca(int s,int v)//找最近公共祖先，并求出最小值
{
    int t1=INF,t2=INF;//两边子树最小值
    if(F(s)!=F(v))return -1;//判断是否连通 
    if(depth[v]>depth[s])//保证s在v下面
        swap(s,v);
    int dh=depth[s]-depth[v];
    for(int i=0;i<=14;i++)//使两个点深度相同 
    {
        if(1<<i&dh)//位运算 
        {
            t1=min(t1,minax[i][s]);
            s=fa[i][s]; 
        }

    } 
    if (s==v) return t1; //判断是否已经满足 
    for(int i=14;i>=0;i--)
    {
        if(fa[i][s]!=fa[i][v])
        {
            t1=min(t1,minax[i][s]);
            t2=min(t2,minax[i][v]);
            s=fa[i][s];
            v=fa[i][v];
        }
    }
    //此时两点都在最近公共祖先的下面，只需再向上走一步 
    t1=min(t1,minax[0][s]);
    t2=min(t2,minax[0][v]);
    return min(t1,t2);
} 

int main()
{
    #ifdef LOCAL 
    freopen("truck.in","r",stdin);
    freopen("truck.out","w",stdout);
    #else
    #endif
    cin>>n>>m;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        e[i*2].from=x;
        e[i*2].to=y;
        e[i*2].d=z;
        e[i*2-1].from=y;
        e[i*2-1].to=x;
        e[i*2-1].d=z;
    }
    sort(e+1,e+2*m+1,com);

    kruskal();

    for(int i=1;i<=2*m;i++)//扫一遍 存使用过的边 
        if(!unuse[i])
        {
            a[e[i].from].push_back(i);
            a[e[i].to].push_back(i);
        }


    for(int i=1;i<=n;i++)
        if(!depth[i])
        {
            int tf=F(i);
            depth[tf]=1;
            dfs(tf);        //dfs建树 
        }
    bz();
    cin>>q;
    for(int i=1;i<=q;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        cout<<lca(x,y)<<'\n';
    }
    return 0;   
}

如果有什么问题，或错误，请在评论区提出，谢谢。