背景:
电商中经常需要计算或预测商品的转化率。点击率r=C/I,考虑两种情况:
1、对于冷启的商品,点击和曝光量都是0,此时,这个商品的CTR应是多少?
2、极端情况下,商品的曝光量是1,点击量是1,此时明显CTR过大。
如何改善计算方法使得计算结果相对准确呢?下面两种方法:威尔逊区间更偏向于统计学习方法,而贝叶斯平滑偏向于机器学习方法,都一定程度上缓解了小样本数据带来的计算准确度不高的情况。
一、威尔逊区间方法(相比于正态分布的置信区间)
1、背景:正态分布置信区间
置信区间是 在一定程度上肯定 包含真实值的取值范围。
例如根据给定样本估计出了一个参数a,那么参数a 的95%的置信区间表示真实的a在某区间内的概率为95%。
举个栗子,我们测量了40个随机选择的男人的身高,结果是平均身高:175cm,标准差:20cm。假设身高符合正态分布,那么95%的置信区间是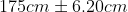 ,也就是从168.8cm到181.2cm。下面解释是如何计算出来的:
,也就是从168.8cm到181.2cm。下面解释是如何计算出来的:
- 首先要有样本数量:40,样本均值:175cm,样本标准差:20cm
- 决定用哪个置信区间,通常是90%,95%,99%,可从标准表中查找对应的Z值。95%的Z值是1.960
将Z值带入置信区间公式: , 其中X是平均身高,z是95%的直线区间对应的Z值1.960,n是样本个数,s是样本标准差。得到结果为
, 其中X是平均身高,z是95%的直线区间对应的Z值1.960,n是样本个数,s是样本标准差。得到结果为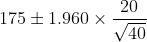 ,即
,即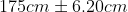 ,也就是从168.8cm到181.2cm,误差界是6.20cm。
,也就是从168.8cm到181.2cm,误差界是6.20cm。
总结:给定身高样本,假设身高服从正态分布,我们估计男人身高值95%的置信区间为[168.8cm, 181.2cm];对于 ,当样本均值和标准差相同时,当n比较大时,得到的误差界会比较小。这表明样本越多,估计值越精确,越趋近于真实的均值。
,当样本均值和标准差相同时,当n比较大时,得到的误差界会比较小。这表明样本越多,估计值越精确,越趋近于真实的均值。
中心极限定理告诉我们,当样本足够多时,任何分布都渐进于正态分布,也就是正态分布近似依赖于中心极限定理。但是这种只适合样本数量较多的情况(np > 5 且 n(1 − p) > 5),对于小样本,准确率不高。
2、威尔逊区间
1927年,美国数学家 Edwin Bidwell Wilson提出了一个修正公式,被称为"威尔逊区间",很好地解决了小样本的准确性问题。

利用威尔逊区间的下限作为点击率,n越小,置信区间越大,得到的点击率越小。当n较大时,点击率接近于p值。
二、贝叶斯平滑
解决上面两个问题,可以利用贝叶斯平滑,分子分母同时加上一个数,可避免上述情况的发生。贝叶斯平滑的思想是给偏好得分预设一个经验初始值,再通过当前的点击量和曝光量来修正这个初始值,在转化率的分子分母中同时加上一个数,可避免上述两个问题,r=(C+a)/(I+b)。若冷启商品的曝光和点击都是0,那么该商品的初始CTR就是这个经验初始值;若商品的曝光量较小,可以通过这个经验初始值来进行修正,适当减少CTR值,使得曝光量大的商品的CTR更可信。
1、贝叶斯估计
我们现在要求的是商品点击率的后验概率。根据贝叶斯公式,需要利用点击率的先验分布和概率密度函数才能得到r的后验分布。

假设:
(1)对于每个商品,是否被点击是一个伯努利分布;(点击为1,未点击为0),商品点击次数服从二项分布。
(2)商品的点击率 r 服从beta分布。
对于假设1,X~Ber(r), r是要估计的参数,则数据的分布是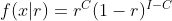 ,其中,
,其中,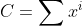 ,若
,若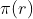 是
是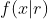 的共轭分布,那么
的共轭分布,那么 有相同的分布。已知二项分布的共轭先验是beta分布,因此我们有假设2 :
有相同的分布。已知二项分布的共轭先验是beta分布,因此我们有假设2 : 。此时,r的后验分布和先验分布是相同的形式。此时,后验分布也服从beta分布,最终后验分布的形式是
。此时,r的后验分布和先验分布是相同的形式。此时,后验分布也服从beta分布,最终后验分布的形式是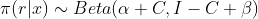 。
。
利用最小化平方差损失函数对参数进行贝叶斯估计,得到r的估计值为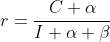 。
。
下面对参数a和b进行参数估计,具体方法:矩估计、极大似然估计
矩估计: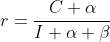 , 由于上面假设r服从beta分布,beta分布的期望是
, 由于上面假设r服从beta分布,beta分布的期望是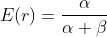 , 方差是
, 方差是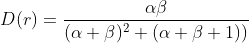 ,可以用历史数据 r 的均值代替期望,r 的方差代替总体的方差,得到
,可以用历史数据 r 的均值代替期望,r 的方差代替总体的方差,得到 的值。
的值。 是偏好均值,
是偏好均值, 是偏好的方差
是偏好的方差
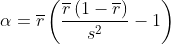
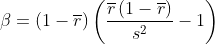
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








