Fourier Transform study note(待更新)

声明：

本学习笔记是糅合多方资料而成，有个人理解的添加，目的仅为个人学习笔记用。

一、傅立叶变换的提出

 

就是这货，叼炸了。。。

       让我们先看看为什么会有傅立叶变换？傅立叶是一位法国数学家和物理学家的名字，英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递很感兴趣，于1807年在法国科学学会上发表了一篇论文，论文里描述运用正弦曲线来描述温度分布，论文里有个在当时具有争议性的决断：任何连续周期信号都可以由一组适当的正弦曲线组合而成。当时审查这个论文的人，其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827)，当拉普拉斯和其它审查者投票通过并要发表这个论文时，拉格朗日坚决反对，在近50年的时间里，拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号，如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望，否定了傅立叶的工作成果，幸运的是，傅立叶还有其它事情可忙，他参加了政治运动，随拿破仑远征埃及，法国大革命后因怕会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。

 

       谁是对的呢？拉格朗日是对的：正弦曲线无法组合成一个带有棱角的信号。但是，我们可以用正弦曲线来非常逼近地表示它，逼近到两种表示方法不存在能量差别，基于此，傅立叶是对的。

 

       为什么我们要用正弦曲线来代替原来的曲线呢？如我们也还可以用方波或三角波来代替呀，分解信号的方法是无穷多的，但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单，因为正余弦拥有原信号所不具有的性质：正弦曲线保真度。一个正余弦曲线信号输入后，输出的仍是正余弦曲线，只有幅度和相位可能发生变化，但是频率和波的形状仍是一样的。且只有正余弦曲线才拥有这样的性质，正因如此我们才不用方波或三角波来表示。

//-----------------------------------------------------------------------------------------------------------------------------------------------------------

注：看到这个地方一开头就晕了，啥叫正弦曲线保真度(sinusoidal fidelity,确切的说是正弦保真度)，为什么就是正弦，方波其他啥的就不行捏？方波得罪傅立叶了么呵呵。。。

看这里：If the input to a linear system is a sinusoidal wave, the output will also be a sinusoidal wave, and at exactly the same frequency as the input.  Sinusoids are the only waveform that have this property.  For instance, there is no reason to expect that a square wave entering a linear system will produce a square wave on the output.——《The Scientist and Engineer's Guide to Digital Signal Processing》第五章，线性系统，Page94

线性系统是啥？ The static response of a linear system is very simple: the output is the input multiplied by a constant—— 《 The Scientist and Engineer's Guide to Digital Signal Processing 》第五章，线性系统，Page92

为什么是正弦，而不是其他，这个归根结底我认为还是Fourier Transform本身的问题，因为一开始就是用正弦逼近的！——傅立叶级数！

高数里面的傅立叶开始发光发热了！哈哈

为什么方波不行？方波用正弦逼近的话，它是由很多不同的正弦逼近的，频率是不同的，它由很多频率不同的正弦函数组成。

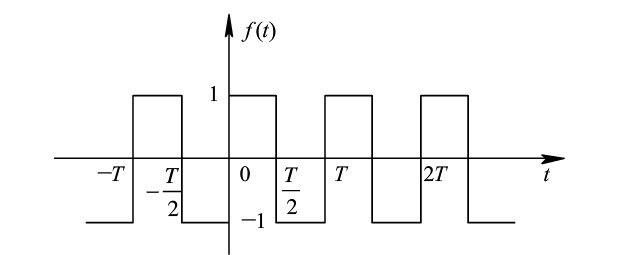
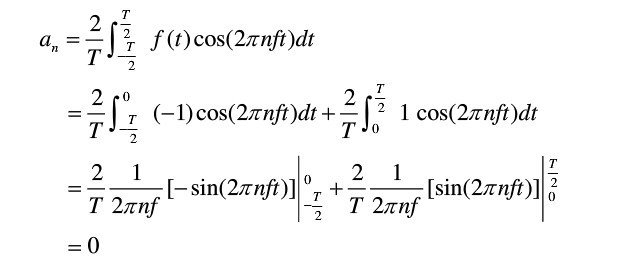
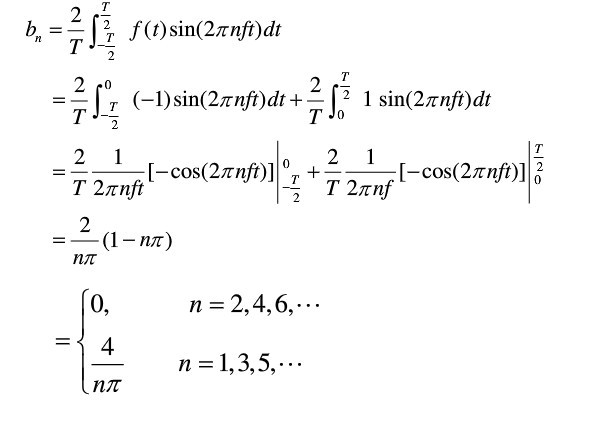
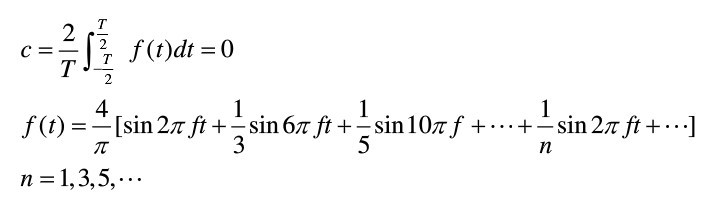
用matlab做个图逼近，玩玩。。。这个仅仅只是当n=10的情况，是不是很“逼近”方波了

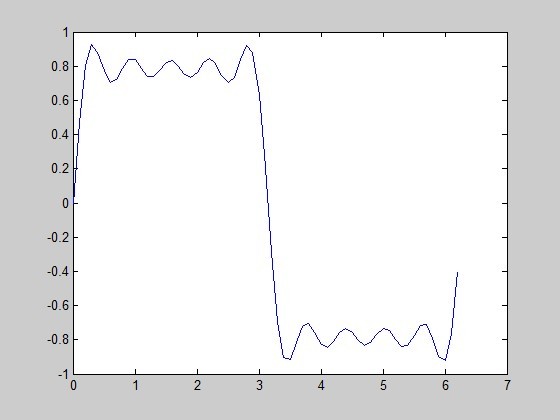
这个是当n = 500的时候，这不就是“方波”了么。。。。傅里叶是不是很屌。。。。这货太聪明了。。。

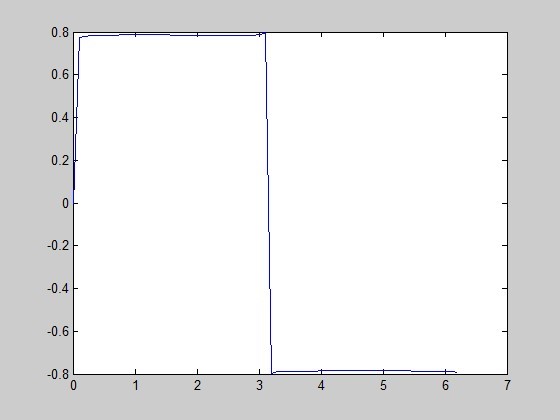
所以到现在，应该很清楚了，对于 曲线保真度 ,方波一开始就是由不同频率的叠加的，所以一开始他的幅值是受到频率的影响的！而sin不同，sin的构造是幅值在外面，而频率在里面很好的“保护起来了”，如果过滤掉组成方波的某些谐波，方波就不是方波了。而正弦不同，正弦的幅值是独立的，不受频率的影响。

 //-----------------------------------------------------------------------------------------------------------------------------------------------------------

二、傅立叶变换分类

 

       根据原信号的不同类型，我们可以把傅立叶变换分为四种类别：

1	非周期性连续信号	傅立叶变换（Fourier Transform）
2	周期性连续信号	傅立叶级数(Fourier Series)
3	非周期性离散信号	离散时域傅立叶变换（Discrete Time Fourier Transform）
4	周期性离散信号	离散傅立叶变换(Discrete Fourier Transform)

       下图是四种原信号图例：  

 

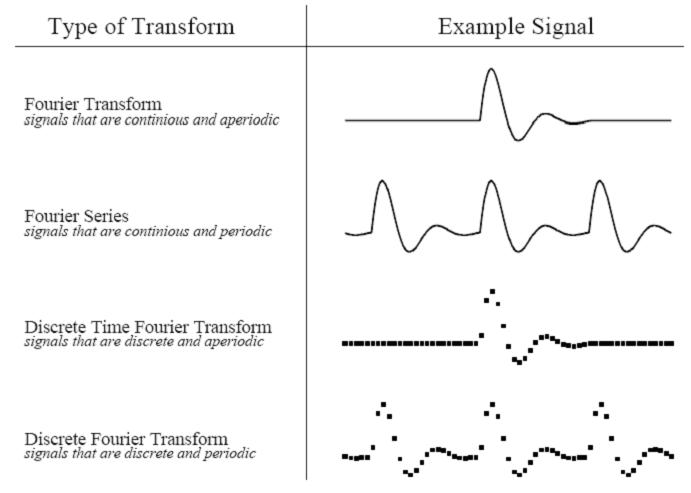
这四种傅立叶变换都是针对正无穷大和负无穷大的信号，即信号的的长度是无穷大的，我们知道这对于计算机处理来说是不可能的，那么有没有针对长度有限的傅立叶变换呢？没有。因为正余弦波被定义成从负无穷小到正无穷大，我们无法把一个长度无限的信号组合成长度有限的信号。面对这种困难，方法是把长度有限的信号表示成长度无限的信号，可以把信号无限地从左右进行延伸，延伸的部分用零来表示，这样，这个信号就可以被看成是非周期性离解信号，我们就可以用到离散时域傅立叶变换的方法。还有，也可以把信号用复制的方法进行延伸，这样信号就变成了周期性离解信号，这时我们就可以用离散傅立叶变换方法进行变换。这里我们要学的是离散信号，对于连续信号我们不作讨论，因为计算机只能处理离散的数值信号，我们的最终目的是运用计算机来处理信号的。

 

       但是对于非周期性的信号，我们需要用无穷多不同频率的正弦曲线来表示，这对于计算机来说是不可能实现的。所以对于离散信号的变换只有离散傅立叶变换（DFT）才能被适用，对于计算机来说只有离散的和有限长度的数据才能被处理，对于其它的变换类型只有在数学演算中才能用到，在计算机面前我们只能用DFT方法，后面我们要理解的也正是DFT方法。这里要理解的是我们使用周期性的信号目的是为了能够用数学方法来解决问题，至于考虑周期性信号是从哪里得到或怎样得到是无意义的。

 

       每种傅立叶变换都分成实数和复数两种方法，对于实数方法是最好理解的，但是复数方法就相对复杂许多了，需要懂得有关复数的理论知识，不过，如果理解了实数离散傅立叶变换(real DFT)，再去理解复数傅立叶变换就更容易了，所以我们先把复数的傅立叶变换放到一边去，先来理解实数傅立叶变换，在后面我们会先讲讲关于复数的基本理论，然后在理解了实数傅立叶变换的基础上再来理解复数傅立叶变换。

 

       还有，这里我们所要说的变换(transform)虽然是数学意义上的变换，但跟函数变换是不同的，函数变换是符合一一映射准则的，对于离散数字信号处理（DSP），有许多的变换：傅立叶变换、拉普拉斯变换、Z变换、希尔伯特变换、离散余弦变换等，这些都扩展了函数变换的定义，允许输入和输出有多种的值，简单地说变换就是把一堆的数据变成另一堆的数据的方法。

三、一个关于实数离散傅立叶变换(Real DFT)的例子

 

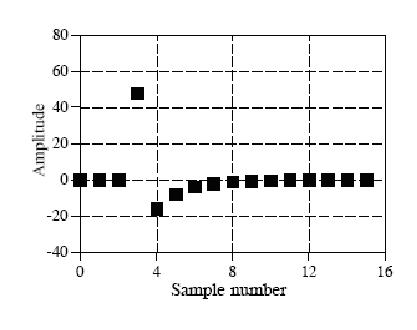
       先来看一个变换实例，下图是一个原始信号图像：

       这个信号的长度是16，于是可以把这个信号分解9个余弦波和9个正弦波（一个长度为N的信号可以分解成N/2+1个正余弦信号，这是为什么呢？结合下面的18个正余弦图,我想从计算机处理精度上就不难理解，一个长度为N的信号，最多只能有N/2+1个不同频率，再多的频率就超过了计算机所能所处理的精度范围），如下图：

       9个余弦信号：

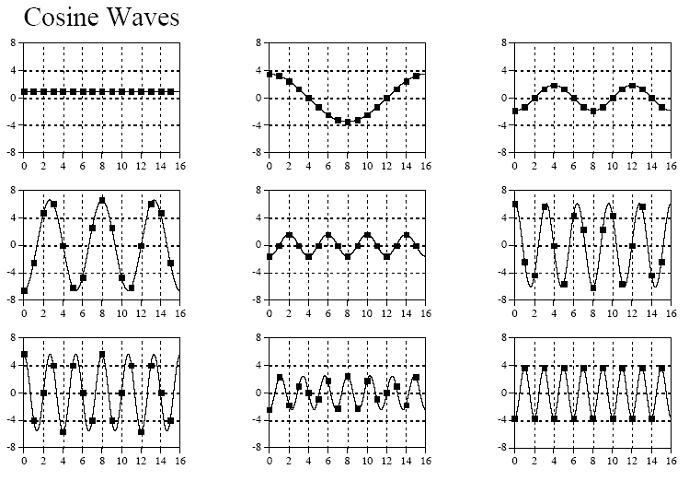
   9个正弦信号：

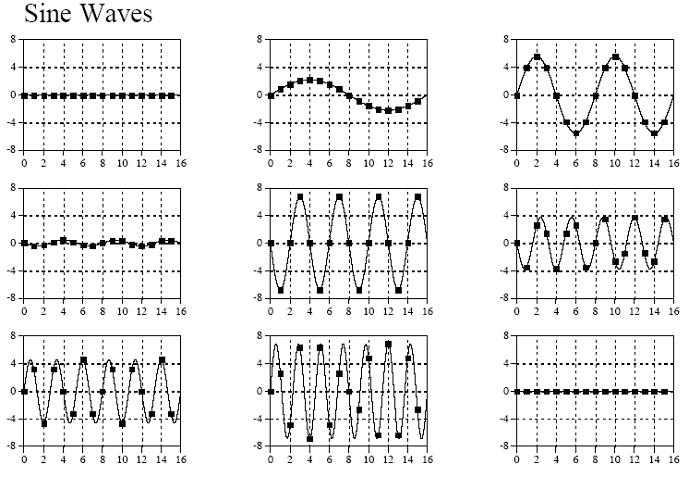
       把以上所有信号相加即可得到原始信号，至于是怎么分别变换出9种不同频率信号的，我们先不急，先看看对于以上的变换结果，在程序中又是该怎么表示的，我们可以看看下面这个示例图：

 

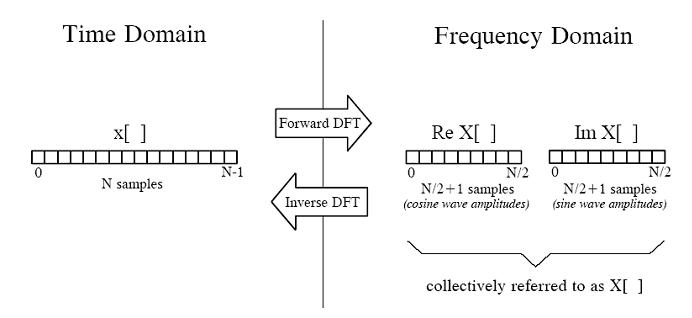
       上图中左边表示时域中的信号，右边是频域信号表示方法，从左向右表示正向转换(Forward DFT)，从右向左表示逆向转换(Inverse DFT)，用小写x[]表示信号在每个时间点上的幅度值数组, 用大写X[]表示每种频率的副度值数组, 因为有N/2+1种频率，所以该数组长度为N/2+1，X[]数组又分两种，一种是表示余弦波的不同频率幅度值：Re X[]，另一种是表示正弦波的不同频率幅度值：Im X[]，Re是实数(Real)的意思，Im是虚数(Imagine)的意思，采用复数的表示方法把正余弦波组合起来进行表示，但这里我们不考虑复数的其它作用，只记住是一种组合方法而已，目的是为了便于表达（在后面我们会知道，复数形式的傅立叶变换长度是N，而不是N/2+1）

------实数形式离散傅立叶变换（Real DFT）

       上一节我们看到了一个实数形式离散傅立叶变换的例子，通过这个例子能够让我们先对傅立叶变换有一个较为形象的感性认识，现在就让我们来看看实数形式离散傅立叶变换的正向和逆向是怎么进行变换的。在此，我们先来看一下频率的多种表示方法。

 

一、          频域中关于频率的四种表示方法

 

1、序号表示方法，根据时域中信号的样本数取0 ~ N/2，用这种方法在程序中使用起来可以更直接地取得每种频率的幅度值，因为频率值跟数组的序号是一一对应的: X[k]，取值范围是0 ~ N/2；

2、分数表示方法，根据时域中信号的样本数的比例值取0 ~ 0.5: X[ƒ]，ƒ = k/N，取值范围是0 ~ 1/2；

3、用弧度值来表示，把ƒ乘以一个2π得到一个弧度值，这种表示方法叫做自然频率(natural frequency)：X[ω]，ω = 2πƒ = 2πk/N，取值范围是0 ~ π；

4、以赫兹(Hz)为单位来表示，这个一般是应用于一些特殊应用，如取样率为10 kHz表示每秒有10,000个样本数：取值范围是0到取样率的一半。

 

二、          DFT基本函数

 

c_k[i] = cos(2πki/N)

s_k[i] = sin(2πki/N)

    其中k表示每个正余弦波的频率，如为2表示在0到N长度中存在两个完整的周期，10即有10个周期，如下图：

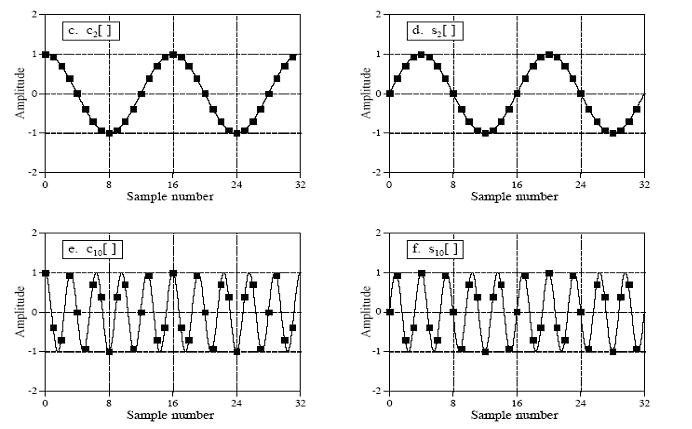
       上图中至于每个波的振幅(amplitude)值(Re X[k],Im X[k])是怎么算出来的,这个是DFT的核心，也是最难理解的部分，我们先来看看如何把分解出来的正余弦波合成原始信号(Inverse DFT)。

 

三、        合成运算方法(Real Inverse DFT)

 

DFT合成等式：

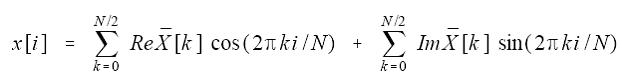
如果有学过傅立叶级数，对这个等式就会有似曾相识的感觉，不错！这个等式跟傅立叶级数是非常相似的：

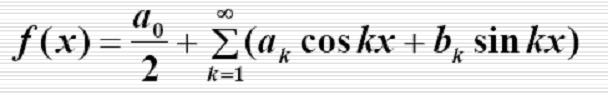
           当然，差别是肯定是存在的，因为这两个等式是在两个不同条件下运用的，至于怎么证明DFT合成公式，这个我想需要非常强的高等数学理论知识了，这是研究数学的人的工作，对于普通应用者就不需要如此的追根究底了，但是傅立叶级数是好理解的，我们起码可以从傅立叶级数公式中看出DFT合成公式的合理性。

 

       DFT合成等式中的Im  [k]和Re  [k]跟Im X[k]和Re X[k]是不一样的，下面是转换方法:

      

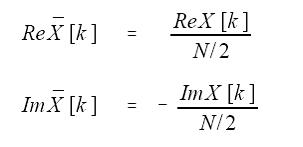
       但k等于0和N/2时,实数部分的计算要用下面的等式:

             

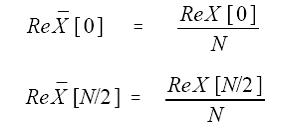
       上面四个式中的N是时域中点的总数，k是从0到N/2的序号。

       为什么要这样进行转换呢？这个可以从频谱密度(spectral density)得到理解，如下图就是个频谱图：

      

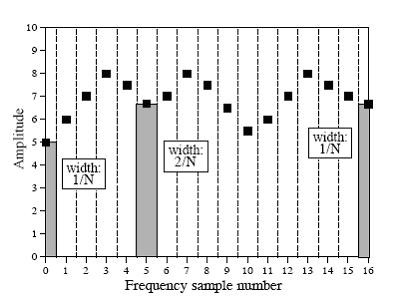
       这是一个频谱图，横坐标表示频率大小，纵坐标表示振幅大小，原始信号长度为N（这里是32），经DFT转换后得到的17个频率的频谱，频谱密度表示每单位带宽中为多大的振幅，那么带宽是怎么计算出来的呢？看上图，除了头尾两个，其余点的所占的宽度是2/N，这个宽度便是每个点的带宽，头尾两个点的带宽是1/N,而Im X[k]和Re X[k]表示的是频谱密度，即每一个单位带宽的振幅大小，但Im  [k]和Re  [k]表示2/N（或1/N）带宽的振幅大小，所以Im  [k]和Re  [k]分别应当是Im X[k]和Re X[k]的2/N（或1/N）。

 

频谱密度就象物理中物质密度，原始信号中的每一个点就象是一个混合物，这个混合物是由不同密度的物质组成的，混合物中含有的每种物质的质量是一样的，除了最大和最小两个密度的物质外，这样我们只要把每种物质的密度加起来就可以得到该混合物的密度了，又该混合物的质量是单位质量，所以得到的密度值跟该混合物的质量值是一样的。

 

       至于为什么虚数部分是负数，这是为了跟复数DFT保持一致，这个我们将在后面会知道这是数学计算上的需要（Im X[k]计算时加上了一个负号，Im  [k]再加上负号，结果便是正的，等于没有变化）。

四、        分解运算方法（DFT）

 

有三种完全不同的方法进行DFT：一种方法是通过联立方程进行求解, 从代数的角度看，要从N个已知值求N个未知值，需要N个联立方程，且N个联立方程必须是线性独立的，但这是这种方法计算量非常的大且极其复杂，所以很少被采用；第二种方法是利用信号的相关性（correlation）进行计算，这个是我们后面将要介绍的方法；第三种方法是快速傅立叶变换（FFT），这是一个非常具有创造性和革命性的的方法，因为它大大提高了运算速度，使得傅立叶变换能够在计算机中被广泛应用，但这种算法是根据复数形式的傅立叶变换来实现的，它把N个点的信号分解成长度为N的频域，这个跟我们现在所进行的实域DFT变换不一样，而且这种方法也较难理解，这里我们先不去理解，等先理解了复数DFT后，再来看一下FFT。有一点很重要，那就是这三种方法所得的变换结果是一样的，经过实践证明，当频域长度为32时，利用相关性方法进行计算效率最好，否则FFT算法效率较高。现在就让我们来看一下相关性算法。

 

利用信号的相关性(correlation)可以从噪声背景中检测出已知的信号，我们也可以利用这个方法检测信号波中是否含有某个频率的信号波：把一个待检测信号波乘以另一个信号波，得到一个新的信号波，再把这个新的信号波所有的点进行相加，从相加的结果就可以判断出这两个信号的相似程度。如下图：

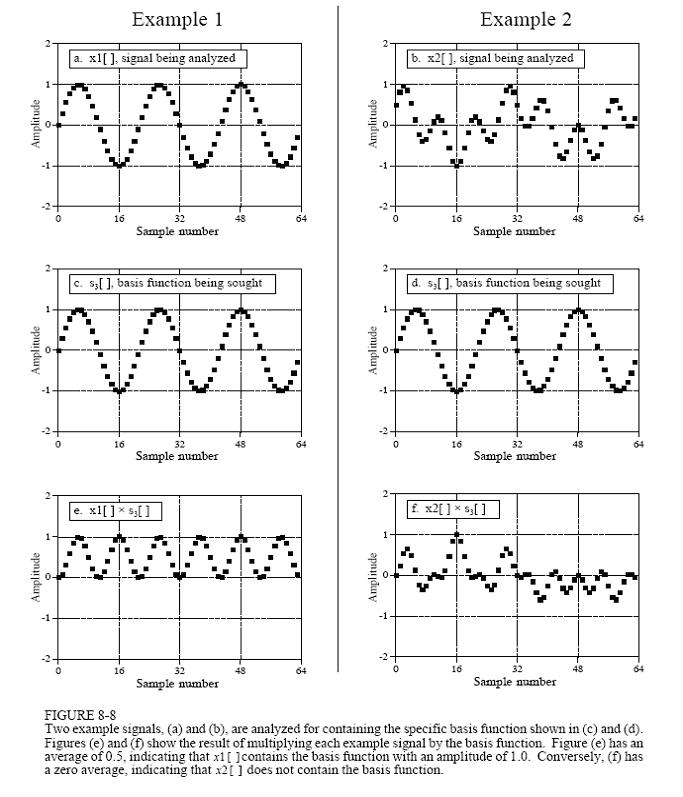
        上面a和 b两个图是待检测信号波，图a很明显可以看出是个3个周期的正弦信号波，图b的信号波则看不出是否含有正弦或余弦信号，图c和d都是个3个周期的正弦信号波，图e和f分别是a、b两图跟c、d两图相乘后的结果，图e所有点的平均值是0.5，说明信号a含有振幅为1的正弦信号c，但图f所有点的平均值是0，则说明信号b不含有信号d。这个就是通过信号相关性来检测是否含有某个信号的方法。

 

       相应地，我也可以通过把输入信号和每一种频率的正余弦信号进行相乘（关联操作），从而得到原始信号与每种频率的关联程度（即总和大小），这个结果便是我们所要的傅立叶变换结果，下面两个等式便是我们所要的计算方法：

      

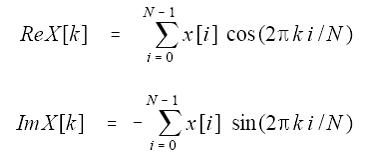
       第二个式子中加了个负号，是为了保持复数形式的一致，前面我们知道在计算Im  [k]时又加了个负号，所以这只是个形式的问题，并没有实际意义，你也可以把负号去掉，并在计算Im  [k]时也不加负号。

 

       这里有一点必须明白一个正交的概念：两个函数相乘，如果结果中的每个点的总和为0，则可认为这两个函数为正交函数。要确保关联性算法是正确的，则必须使得跟原始信号相乘的信号的函数形式是正交的，我们知道所有的正弦或余弦函数是正交的，这一点我们可以通过简单的高数知识就可以证明它，所以我们可以通过关联的方法把原始信号分离出正余弦信号。当然，其它的正交函数也是存在的，如：方波、三角波等形式的脉冲信号，所以原始信号也可被分解成这些信号，但这只是说可以这样做，却是没有用的。

背景知识——相关性算法
-------------
这个算法用来检测两个波形的相似程度。“啥叫相似程度？”
举例说明：

上面两个波形是相似的（看上去差不多，周期基本对应）


上面两个波形比较相似，因为其中一个加了噪音，所以没有第一组相似度高。


上面两个波形的相似度很低。

那么相关性算法就是可以求出描述【相似程度】的【具体的值】的算法。

其实非常简单，把两个波形对应时间上的采样乘起来，乘得的值累加起来就行了：
Sum = 0;
for(i = 0;i < Size;i ++)
{
Sum += Wave1[i] * Wave2[i];
}
最后Sum就是两个波形的相似程度。

为什么乘法这么神奇呢？
我们设想一下极端情况：
1. 当被乘的两个采样一正一负，乘积为负。
2. 当被乘的两个采样都是正，乘积为正。
3. 当被乘的两个采样都是负，乘积为正。
乘法的奥秘在于两个采样差得小时，乘积相对差得远时会大（大多数情况）。

补充：这个相关算法没有考虑相位的变化，即使相同信号，对应位置发生偏移时，计算得出的相似程度也会变低

【二】离散傅立叶变换
在介绍快速傅立叶变换之前，先介绍一下快速傅立叶变换的基础：离散傅立叶变换（DFT）。
对同样的输入，执行相同大小的FFT和DFT，其输出是相同的，区别仅在于快速傅立叶变换速度更快（但适用范围一般会变窄）。
我们之所以用FFT而不是DFT是因为DFT的速度慢得令人难以接受，尤其是进行大规模的变换时，DFT的速度会比FFT慢数万倍！

傅立叶变换的作用可以简单解释为“求出给定波形中不同频率的含量”。
但注意这是【简单】解释不是【准确】解释。
我觉得解释为“求出波形和不同频率正弦、余弦波形的相关性”更加合适。上面提到“不同频率的含量”，其实是对这些sin cos波形的相关度作处理得到的。本帖最后会提到具体方法。

注意上面我直接用相关性描述了傅立叶变换，那么它已经被简化成我们知识范围内的东西了。

<=帮你回顾一下sin和cos的波形。

前面提到，FFT是DFT优化后的快速形式。其实实现FFT的算法有很多种，它们的适用范围不一样，速度也不一样。大多数FFT算法的思想是把一次大的DFT分割成几个小的DFT，这样递归式地细分下去……
上面的代码中可以看出来，DFT的复杂度是O(n^2)，那么n缩小的话，FFT的效率必然会比DFT提高，不严谨地说，如果FFT能把一次DFT拆成两个一半大小的DFT，FFT的复杂度理论上应该是O(n * log(n))。

最常用的FFT算法是Cooley和Turkey提出的Radix-2 FFT（基-2FFT），即上面所讲的把一个DFT拆成两个一半大小的DFT。此方法因为实现简单倍受欢迎。Radix-2 FFT适用于N为2的整数次方的FFT。
此外还有Radix-4，Radix-8 FFT，它们效率更高，但适用范围太窄。
综合了Radix-2的适用范围和Radix-4的效率的算法是SplitRadix FFT（分裂基FFT），名字听上去就很帅，实际玩起来也挺帅的……效率比Radix2快零点几倍吧大概，但实现起来复杂很多。

【三】基2FFT的实现

这里不得不用一下数学了，不然没法解释……
我尽量用简单的方式说明。

先抛开推导和证明，看一下Radix2怎么把一次大DFT拆成两个小DFT的：
给定输入信号Wave[],
Step1：把Wave[]按奇偶拆成Wave1[]和Wave2[]两组：
Wave1[0] = Wave[0];
Wave2[0] = Wave[1];
Wave1[1] = Wave[2];
Wave2[1] = Wave[3];
Wave1[2] = Wave[4];
Wave2[2] = Wave[5];
……
Step2：分别对Wave1[]和Wave2[]进行DFT，输出到ComplexWave1[]和ComplexWave2[]数组（假定这两个输出的数组可以存放复数）
Step3：

好吧，这个公式涉及一个复数乘法。
怎么做复数乘法？
如果我们做一个二项式乘法，如(a + b)(c + d)，结果是ac + ad + bc + bd。那么做(a + bi)(c + di)这种复数乘法时方法一样，直接拿bi和di替换掉b和d，就是你要的结果了。注意i * i = -1，因为i是根号-1。
(a + bi)(c + di) = a * c - b * d + i(a * d + c * b)
结果还是个复数。

我们先来看DFT的公式：
 （摘自维基）
看到这个别怕，我们来一步一步剖析它的含义。
首先是各变量定义：
x是一个数组，代表输入的数据，值为复数形式（如果你输入了实数，给每个实数加个 0i 的虚数部分就变复数形式了）。xn的意思就是x[n]，比如n=1时，xn就是x[1]。
X是输出的数组，值的形式也是复数。Xk就是X[k]的意思。
N是DFT变换的大小。
e自然对数。它类似于Pi，是个无限不循环小数常量，值为2.718左右。它在进行幂运算时有些特殊性质。
n在这里是个“循环变量”。

如果你知道怎么算这条公式的话，把x k N带进去就能算出结果。下面来剖析一下计算过程。
把Sigma转换成循环体，

要算出整个数组X，你需要在这个循环外面套一个for(k = 0;k < N; k++)

你肯定觉得奇怪：e的虚数次方到底是怎么算的？ 我们有欧拉公式可以轻松地化解这个问题。

接下来用数学描述FFT的过程：




我记得初中教了幂运算……

神奇的事情发生了：