数据结构 | 3.树与二叉树

最新推荐文章于 2025-02-09 13:17:44 发布
最新推荐文章于 2025-02-09 13:17:44 发布
阅读量2.7k 收藏 2
点赞数
分类专栏： 数据结构 文章标签： c语言 数据结构 算法 树和二叉树
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/u011386173/article/details/120179562
版权
本文介绍了树的基本概念，包括树的深度、高度和度，重点讲解了二叉树的性质，如度为0的结点比度为2的结点多1个，并展示了二叉树的遍历方式。此外，讨论了如何从广义表构建二叉树，以及二叉搜索树的插入、遍历和相关LeetCode题目，如相同树、对称二叉树、层序遍历等。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

在 栈和队列 一文中提到，栈可以处理具有 完全包含 关系的问题。

而树分为两部分：结点 和 边。结点可以理解为集合，边称为关系。树的根结点就叫做全集，子节点叫做子集，子集并起来就得到了全集。

根结点就是待解决的问题，可能是个大问题，可以划分为多个子问题，即是子结点。

树也存在着一种完全包含关系。树和栈是有一定关联的，遍历树的时候就要使用栈，而且使用到的是系统栈，用到系统栈的表现形式就是递归。

1、树的深度、高度和度

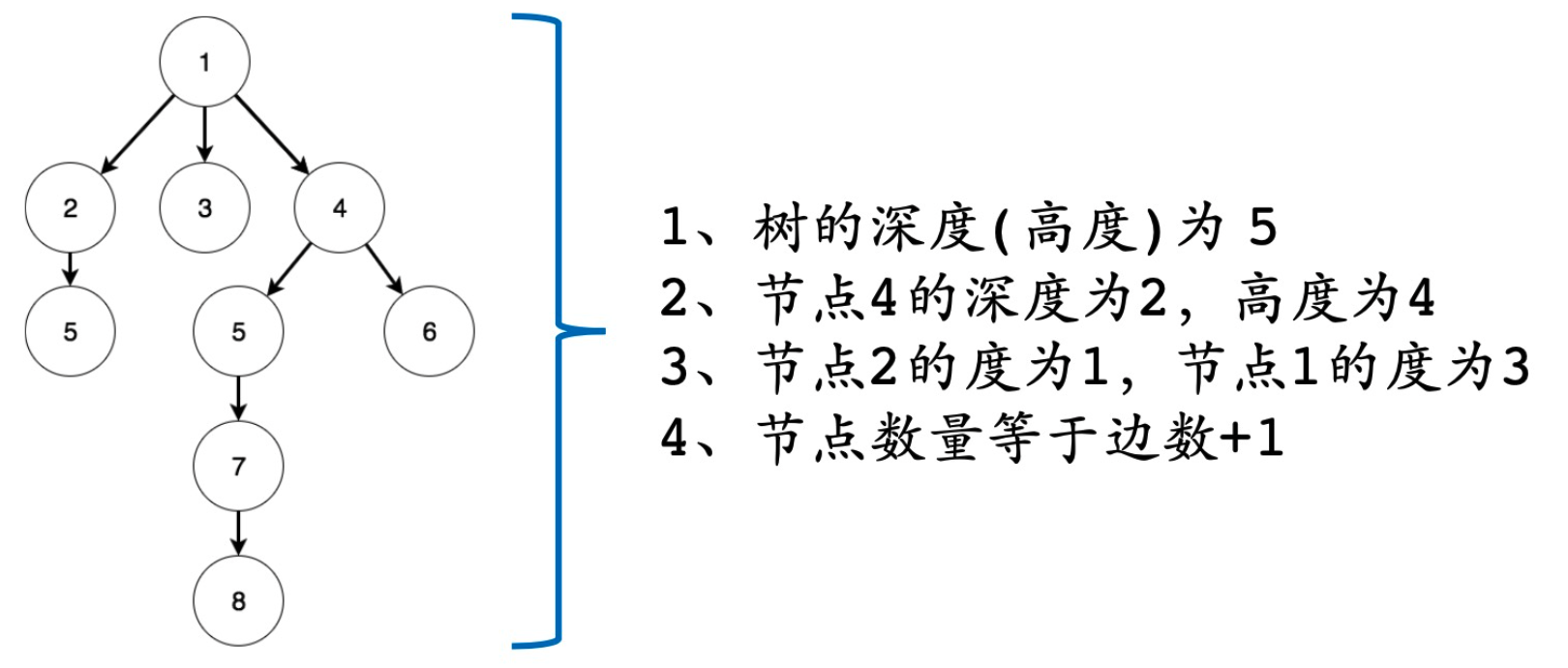
image-20201102153435159
  • 树的根结点所在层数为第一层。结点下有几个子结点，度就为几。
  • 深度 是从根往下的层数，高度 是从最后一层往上到该结点的层数。
  • 结点数量 = 边数 + 1

2、二叉树

计算机底层是用二进制存储的，二进制可以表示任何进制的数。同理，二叉树可以表示任意多的树形结构。
通过 左孩子-右兄弟（十字链表法）的表示法，可以将任意的树形结构转化成二叉树。

如上面的三叉树转化为二叉树如下所示：
image-20201102174114763
N N N 叉树是一个非确定性问题，但是可以使用二叉树来实现，即是将一个非确定性问题转换为了一个确定性问题。所以如果要实现 N N N 叉树，不需要问 N N N 是多少，只需要实现二叉树的结构定义即可，因为任何形式的树形结构都能转化成二叉树形式。

3、二叉树的性质

image-20201102153513418
  • 度为 0 的结点称为叶子结点
  • “度为 0 的结点比度为 2 的结点多 1 个”结论的推导依据：结点个数 = 边数+ 1

推导过程： n 1 + n 0 + n 2 ( 结 点 数 ） = n 1 + 0 + 2 ∗ n 2 + 1 ( 边 数 ) n_1 + n_0 + n_2(结点数）= n_1 + 0 + 2 * n_2 + 1 (边数) n1​+n0​+n2​(结点数）=n1​+0+2∗n2​+1(边数) => n 0 = n 2 + 1 n_0 = n_2 + 1 n0​=n2​+1。
其中， n 1 n_1 n1​ 表示度为 1 的结点个数， n 0 n_0 n0​ 表示度为 0 的结点个数， n 2 n_2 n2​ 表示度为 2 的结点个数。
n 0 = n 2 + 1 n_0 = n_2 + 1 n0​=n2​+1，即度为 0 的结点比度为 2 的结点多 1 个。

4、二叉树的遍历方式

遍历即访问每个结点。
image-20201102153614987

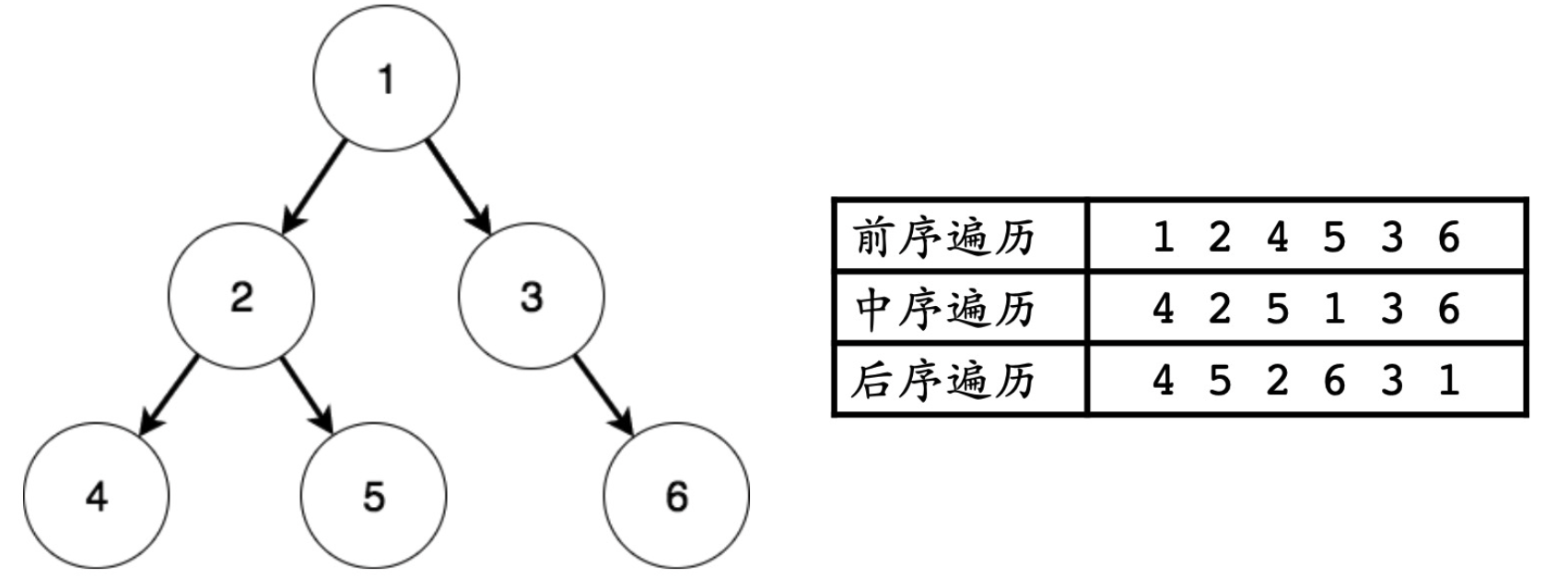
image-20201102153645141

5、中国版二叉树和国际版二叉树

  • 中国版二叉树
    image-20201102153730891
  • 国际版二叉树
    image-20201102153802853

满二叉树：只存在度为 0 和度为 2 的结点。

6、 完全二叉树

image-20201102153832125
因为子结点的编号是连续的，所以可以使用连续空间存储。

可以根据当前结点的编号，计算出它的左右孩子的编号。即完全二叉树可以用数组实现，每个结点可以从记录式变为计算式。

7、广义表

image-20201102153858978 image-20201102153942857

上图的右侧为该树的几种广义表表示方法，通常都是使用前两种，因为更直观。

8、广义表转二叉树的代码实现

【要求】将广义表还原构建为一棵二叉树。

【思路】广义表是用括号嵌套来表示的，而对于括号这样的问题，可以使用栈来解决。根据左括号入栈、右括号出栈。从左到右遍历字符串，遇到非括号字符封装成一个二叉树结点信息，记录该结点的地址，遇到左括号，将当前结点入栈；下一个非括号字符也封装成一个二叉树结点，其父节点就是栈顶元素，需要判断它是左孩子还是右孩子，可以根据逗号，如果没遇到逗号，就是左孩子，取出栈顶元素，将栈顶元素的左孩子的指向该结点。遇到右括号，出栈。
【代码】

// 广义表转二叉树

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

/*
 * 【要求】将广义表还原构建为一棵二叉树。
 * 【思路】
 * 广义表是用括号嵌套来表示的，而对于括号这样的问题，可以使用栈来解决。根据左括号入栈、右括号出栈。
 * 从左到右遍历字符串，遇到非括号字符封装成一个二叉树结点信息，记录该结点的地址，遇到左括号，将当前结点入栈；下一个非括号字符也封装成一个二叉树结点，其父节点就是栈顶元素。
 * 需要判断它是左孩子还是右孩子，可以根据逗号。如果没遇到逗号，就是左孩子，取出栈顶元素，将栈顶元素的左孩子的指向该结点；遇到右括号，出栈。
 */

typedef struct Node { //二叉树结点
    char data;
    struct Node *lchild, *rchild;
} Node;

typedef struct Tree {
    Node *root; //根结点
    int n; //当前节点个数
} Tree;

typedef struct Stack {
    Node **data; //开辟一片连续的存储空间，每个位置都是存储的Node *这样的地址
    int top; //栈顶
    int capacity; //容量
} Stack;

/*
 * 树结点的创建
 */
Node *createNewNode(char val) { 
    Node *p = (Node *)malloc(sizeof(Node));
    p->data = val;
    p->lchild = NULL;
    p->rchild = NULL;
    return p;
}

/*
 * 树的初始化
 */
Tree *initTree() {
    Tree *tree = (Tree *)malloc(sizeof(Tree));
    tree->root = NULL;
    tree->n = 0;
    return tree;
}

/*
 * 栈的初始化
 */
Stack *initStack(int n) {
    Stack *s = (Stack *)malloc(sizeof(Stack));
    s->data = (Node **)malloc(sizeof(Node *) * n);
    s->top = -1;
    s->capacity = n;
    return s;
}

/*
 * 获取栈顶元素
 */
Node *top(Stack *s) {
    return s->data[s->top];
}


/*
 * 判断栈是否为空
 */
int isEmpty(Stack *s) {
    return s->top == -1;
}

/*
 * 入栈
 */
int push(Stack *s, Node *val) {
    if (s == NULL) return -1;
    if (s->top == s->capacity - 1) return -1;
    s->data[++(s->top)] = val;
    return 0;
}


/*
 * 出栈
 */
int pop(Stack *s) {
    if (s == NULL) return -1;
    if (isEmpty(s)) return -1;
    s->top--;
    return 0;
}

/*
 * 栈的销毁
 */
void destroyStack(Stack *s) {
    if (s == NULL) return ;
    free(s->data);
    free(s);
    return ;
}

/*
 * 二叉树结点的销毁
 */
void destroyNode(Node *node) {
    if (node == NULL) return ;
    destroyNode(node->lchild);
    destroyNode(node->rchild);
    free(node);
    return ;
 }

/*
 * 二叉树的销毁
 */
void destroyTree(Tree *tree) {
    if (tree == NULL) return ;
    destroyNode(tree->root);
    free(tree);
    return ;
}

/*
 * 广义表转二叉树
 */
 Node *buildNode(const char *str, int *node_cnt) {
    Stack *s = initStack(strlen(str));
    Node *temp = NULL;
    Node *p = NULL; //p记录根结点，即栈中最后弹出的元素
    int flag = 0;
    while (str[0]) {
        switch (str[0]) {
            case '(':
                push(s, temp);
                flag = 0;
                break;
            case ')':
                p = top(s);
                pop(s);
                break;
            case ',':
                flag = 1;
                break;
            case ' ': 
                break;
            default:
                temp = createNewNode(str[0]);
                if (!isEmpty(s) && flag == 0) {
                    top(s)->lchild = temp;
                } else if (!isEmpty(s) && flag == 1) {
                    top(s)->rchild = temp;
                }
                ++(*node_cnt);
                break;
        }
        ++str;
    }
    if (p == NULL) p = temp; //只有一个结点时因为没有括号，就没有了入栈操作，故单独判断这种情况 
    destroyStack(s);
    return p;
}

/*
 * 先序遍历
 */
void pre_order_node(Node *node) {
    if (node == NULL) return ;
    printf("%c ", node->data);
    pre_order_node(node->lchild);
    pre_order_node(node->rchild);
    return ;
}

/*
 * 先序遍历：传入根结点
 */
void pre_order(Tree *tree) {
    if (tree == NULL) return ;
    printf("pre_order: ");
    pre_order_node(tree->root);
    printf("\n");
    return ;
}


/*
 * 中序遍历
 */
void in_order_node(Node *node) {
    if (node == NULL) return ;
    in_order_node(node->lchild);
    printf("%c ", node->data);
    in_order_node(node->rchild);
    return ;
}


void in_order(Tree *tree) {
    if (tree == NULL) return ;
    printf("in_order: ");
    in_order_node(tree->root);
    printf("\n");
}

/*
 * 后序遍历
 */
void post_order_node(Node *node) {
    if (node == NULL) return ;
    post_order_node(node->lchild);
    post_order_node(node->rchild);
    printf("%c ", node->data);
    return ;
}

void post_order(Tree *tree) {
    if (tree == NULL) return ;
    printf("post_order: ");
    post_order_node(tree->root);
    printf("\n");
    return ;
}


int main() {
    char str[1000] = {0};
    int node_cnt = 0;
    scanf("%[^\n]s", str);
    Tree *tree = initTree(); //二叉树初始化
    tree->root = buildNode(str, &node_cnt); //广义表转二叉树结点
    tree->n = node_cnt;
    pre_order(tree);
    in_order(tree);
    post_order(tree);
    destroyTree(tree);
    return 0;
}

测试结果：

A(B(,D),C(E,)) # 输入
pre_order: A B D C E
in_order: B D A E C
post_order: D B E C A

9、二叉搜索树的代码实现

二叉搜索树的特点：左子树结点的值 < 根结点的值 < 右子树结点的值。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

/*
 * 二叉搜索树结点定义
 */
typedef struct Node {
    int val;
    struct Node *lchild;
    struct Node *rchild;
} Node;

/*
 * 树的结构定义
 */
typedef struct Tree {
    Node *root;
    int cnt;
} Tree;

/*
 * 结点初始化
 */
Node *init_node(int val) {
    Node *node = (Node *)malloc(sizeof(Node));
    node->val = val;
    node->lchild = NULL;
    node->rchild = NULL;
    return node;
}

/*
 * 树的初始化
 */
Tree *init_tree() {
    Tree *tree = (Tree *)malloc(sizeof(Tree));
    tree->root = NULL;
    tree->cnt = 0;
    return tree;
}

/*
 * 销毁结点
 */
void destroy_node(Node *node) {
    if (node == NULL) return ;
    destroy_node(node->lchild);
    destroy_node(node->rchild);
    free(node);
    return ;
}

/*
 * 销毁树
 */
void destroy_tree(Tree *tree) {
    if (tree == NULL) return ;
    destroy_node(tree->root);
    free(tree);
    return ;
}

/*
 * 结点的插入
 */
Node *insert_node(Node *root, int val, int *flag) {
    if (root == NULL) {
        *flag = 1;
        return init_node(val);
    }
    if (root->val == val) return root; //待插入的值与根节点值相等，不做任何插入操作
    if (val < root->val)  //待插入的值比根节点值小，则要插在左子树上
        root->lchild = insert_node(root->lchild, val, flag);
    else //待插入的值比根节点值大，则要插在右子树上
        root->rchild = insert_node(root->rchild, val, flag);
    return root;
}

/*
 * 插入操作
 */
void insert(Tree *tree, int val) {
    int flag = 0;
    tree->root = insert_node(tree->root, val, &flag);
    tree->cnt += flag; //如果flag = 1，表示插入成功，更新节点数
    return ;
}

/*
 * 先序遍历
 */
void pre_order_node(Node *node) {
    if (node == NULL) return ;
    printf("%d ", node->val);
    pre_order_node(node->lchild);
    pre_order_node(node->rchild);
    return ;
}


void pre_order(Tree *tree) {
    if (tree == NULL) return ;
    printf("pre_order: ");
    pre_order_node(tree->root);
    printf("\n");
    return;
}

/*
 * 中序遍历
 */
void in_order_node(Node *node) {
    if (node == NULL) return ;
    in_order_node(node->lchild);
    printf("%d ", node->val);
    in_order_node(node->rchild);
    return ;
}


void in_order(Tree *tree) {
    if (tree == NULL) return ;
    printf("in_order: ");
    in_order_node(tree->root);
    printf("\n");
    return;
}

/*
 * 后序遍历
 */
void post_order_node(Node *node) {
    if (node == NULL) return ;
    post_order_node(node->lchild);
    post_order_node(node->rchild);
    printf("%d ", node->val);
    return ;
}


void post_order(Tree *tree) {
    if (tree == NULL) return ;
    printf("post_order: ");
    post_order_node(tree->root);
    printf("\n");
    return;
}

/*
 * 节点值的打印
 */
void output_node(Node *node) {
    if (node == NULL) return ;
    printf("%d", node->val);
    if (node->lchild == NULL && node->rchild == NULL) return ;
    printf("(");
    output_node(node->lchild);
    printf(",");
    output_node(node->rchild);
    printf(")");
    return ;
}

/*
 * 二叉树转广义表
 */
void output(Tree *tree) {
    if (tree == NULL) return ;
    printf("tree(%d) : ", tree->cnt);
    output_node(tree->root);
    printf("\n");
    return ;
}


int main() {
    srand(time(0));
    Tree *tree = init_tree();
    #define max_op 10
    for (int i = 0; i < max_op; i++) {
        int val = rand() % 100;
        insert(tree, val);
        output(tree);
    }
    pre_order(tree);
    in_order(tree);
    post_order(tree);
    #undef max_op
    destroy_tree(tree);

    return 0;
}

测试结果：

tree(2) : 7(,62)
tree(3) : 7(,62(48,))
tree(4) : 7(,62(48(19,),))
tree(5) : 7(,62(48(19,),68))
tree(6) : 7(,62(48(19,),68(,90)))
tree(7) : 7(6,62(48(19,),68(,90)))
tree(8) : 7(6,62(48(19(17,),),68(,90)))
tree(9) : 7(6,62(48(19(17,),),68(,90(71,))))
tree(10) : 7(6,62(48(19(17,),53),68(,90(71,))))
pre_order: 7 6 62 48 19 17 53 68 90 71
in_order: 6 7 17 19 48 53 62 68 71 90
post_order: 6 17 19 53 48 71 90 68 62 7

10、相关题目

Leetcode 100.相同的树

【思路】判断两棵树是否相同，就是判断两棵树的各个结点的数据域是否相同，于是需要遍历比较两棵树的相同位置的结点，当然需要使用到递归，递归结束的边界条件就是当前比较的两个结点存在的各种情况。
【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool isSameTree(struct TreeNode* p, struct TreeNode* q){
    if (p == NULL && q == NULL) return true;
    if (p == NULL || q == NULL) return false;
    if (p->val != q->val) return false;
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

Leetcode 101.对称二叉树

【思路】和Leetcode 100 是相同的思路，不过是对称地进行比较。
【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

bool isSame(struct TreeNode *left_node, struct TreeNode *right_node) {
    if (left_node == NULL && right_node == NULL) return true;
    if (left_node == NULL || right_node == NULL || left_node->val != right_node->val) return false;
    return isSame(left_node->left, right_node->right) && isSame(left_node->right, right_node->left);
}

bool isSymmetric(struct TreeNode* root){
    return isSame(root->left, root->right);
}

Leetcode 102.二叉树的层序遍历

【思路】BFS，但是和一般的BFS的区别在于，每次并不只是只出队一个元素，而是出队同一层的所有元素。
【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
//1.判断一层结束:同一层元素处理完毕之后进行下一次迭代，迭代次数就是层数
//2.每层的节点个数：当前队列中的元素个数
//returnSize记录结果中二维数组的行数，returnColumnSizes记录每行的个数
#define max 1024
int** levelOrder(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
    if (root == NULL) {
        *returnSize = 0;
        return NULL;
    }
    //队列存放树节点
    struct TreeNode *queue[max]; //静态数组
    int head = 0, tail = 0;

    int **ans = malloc(sizeof(int *) * max);
    *returnColumnSizes = malloc(sizeof(int) * max);

    int level = 0, count = 0; //level为层数
    queue[tail++] = root; //根节点入队
    count++;

    while (head != tail) {
        count = tail - head; //当前队列中的元素个数
        (*returnColumnSizes)[level] = count; //记录当前层的元素个数
        //存储当前层的元素
        ans[level] = malloc(sizeof(int) * count);
        //相比于普通的队列出队，这里是将同一层的元素全部出队
        for (int i = 1; i <= count; i++) { //出队同一层的元素
            struct TreeNode *p = queue[head++];
            ans[level][i - 1] = p->val;
            if (p->left) queue[tail++] = p->left; //入队刚刚出队元素的左孩子子结点
            if (p->right) queue[tail++] = p->right;
        }
        level++;
    }
    *returnSize = level; //记录总的层数
    return ans;
}

Leetcode 104. 二叉树的最大深度

【思路】递归遍历二叉树节点，同时记录深度。
【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int ans = 0;
    void func(TreeNode *p, int depth) {
        if (p == nullptr) return ;
        ans = max(ans, depth);
        func(p->left, depth + 1);
        func(p->right, depth + 1);
    }

    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;
        func(root, 1);
        return ans;
    }
};

Leetcode 107. 二叉树的层序遍历 II

【思路】思路同Leetcode102题，只是最后将结果进行反转。
【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


/**
 * Return an array of arrays of size *returnSize.
 * The sizes of the arrays are returned as *returnColumnSizes array.
 * Note: Both returned array and *columnSizes array must be malloced, assume caller calls free().
 */
 #define max 1024
int** levelOrderBottom(struct TreeNode* root, int* returnSize, int** returnColumnSizes){
    if (root == NULL) {
        *returnSize = 0;
        return NULL;
    }

    struct TreeNode **queue = (struct TreeNode **)malloc(sizeof(struct TreeNode *) * max);
    int head = 0, tail = 0, count = 0, level = 0;

    *returnColumnSizes = malloc(sizeof(int) * max);//一维数组
    int **ans = (int **)malloc(sizeof(int *) * max);

    queue[tail++] = root;
    count++;

    while (head != tail) {
        count = tail - head; //每层节点个数
        (*returnColumnSizes)[level] = count; //记录level层的节点个数
        ans[level] = malloc(sizeof(int) * count);//开辟空间存储每一层的每个节点
    
        for (int i = 1; i <= count; i++) {
            struct TreeNode *p = queue[head++];
            ans[level][i - 1] = p->val;
            if (p->left) queue[tail++] = p->left;
            if (p->right) queue[tail++] = p->right;
        }
        level++;
    }
    *returnSize = level;

    for (int i = 0, j = level- 1; i < j; i++, j--) {
        //交换层
        int *temp1 = ans[i];
        ans[i] = ans[j];
        ans[j] = temp1;
        //交换每一层的节点个数
        int *temp2 = (*returnColumnSizes)[i];
        (*returnColumnSizes)[i] = (*returnColumnSizes)[j];
        (*returnColumnSizes)[j] = temp2;
    }

    return ans;

}

Leetcode 110.平衡二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

int height(struct TreeNode *root) {
    if (root == NULL) {
        return 0;
    } 
    return fmax(height(root->left), height(root->right)) + 1;
}


bool isBalanced(struct TreeNode* root){
    if (root == NULL) return true;
    return fabs(height(root->left) - height(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
}

Leetcode 111.二叉树的最小深度

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

//深搜 DFS
int minDepth(struct TreeNode* root){
    if (root == NULL) return 0;
    if (root->left == NULL && root->right == NULL) return 1;

    int ans = INT_MAX;

    if (root->left != NULL) ans = fmin(ans, minDepth(root->left));
    if (root->right != NULL) ans = fmin(ans, minDepth(root->right));

    return ans + 1;
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

//广搜：此处使用了数组实现队列，可以使用链表实现更节省空间
struct QueueNode {
    int head, tail;
    struct TreeNode **data;
    int capacity;
};

struct QueueNode *init(int n) {
    struct QueueNode *node = (struct QueueNode *)malloc(sizeof(struct QueueNode));
    node->head = 0;
    node->tail = 0;
    node->data = (struct TreeNode **)malloc(sizeof(struct TreeNode *) * n);
    node->capacity = n;
    return node;
}

int minDepth(struct TreeNode* root){
    if (root == NULL) return 0;
    if (root->left == NULL && root->right == NULL) return 1;
    
    struct QueueNode *que = init(100000);
    que->data[(que->tail)++] = root;
    int depth = 1;
    while (que->head != que->tail) {
        int size = (que->tail - que->head); //计算队列中的元素
        for (int i = 0; i < size; i++) { //处理每层的节点
            struct TreeNode *temp = que->data[que->head++];
            if (temp->left != NULL) {
                que->data[(que->tail)++] = temp->left;
            }
            if (temp->right != NULL) {
                que->data[(que->tail)++] = temp->right;
            }

            if (temp->left == NULL && temp->right == NULL) {
                return depth;
            }
        }
        depth++;
    }
    return false;
}

Leetcode 112. 路径总和

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


bool hasPathSum(struct TreeNode* root, int targetSum){
    if (root == NULL) return false;
    if (root->left == NULL && root->right == NULL && root->val == targetSum) return true;

    return hasPathSum(root->left, targetSum - root->val) || hasPathSum(root->right, targetSum - root->val);
}

Leetcode 226. 翻转二叉树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode* invertTree(struct TreeNode* root){
    if (root == NULL) return NULL;
    struct TreeNode *left = root->left;
    root->left = root->right;
    root->right = left;
    invertTree(root->left);
    invertTree(root->right);
    return root;
}

Leetcode 235. 二叉搜索树的最近公共祖先

【思路】一次遍历。利用二叉搜索树的性质，分为三种情况：

  1. 如果当前节点大于 p 和 q 的值，则 p 和 q 的最近公共祖先在当前节点的左子树；
  2. 如果当前节点小于 p 和 q 的值，则 p 和 q的最近公共祖先在当前节点的右子树；
  3. 如果上述情况都不满足，则当前节点就是"分岔节点"，此时要么 p和 q 在当前节点的不同子树中，要么其中一个节点就是当前节点。

【代码】

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

struct TreeNode* lowestCommonAncestor(struct TreeNode* root, struct TreeNode* p, struct TreeNode* q) {
    struct TreeNode *ancestor = root;
    while (true) {
        if (ancestor->val > p->val && ancestor->val > q->val) {
            ancestor = ancestor->left;
        } else if (ancestor->val < p->val && ancestor->val < q->val) {
            ancestor = ancestor->right;
        } else {
            break;
        }
    }
    
    return ancestor;
}

Leetcode 257.二叉树的所有路径

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //深搜
    void construct_paths(TreeNode *root, string path, vector<string> &paths) {
        if (root != nullptr) {
            path += to_string(root->val);
            if (root->left == nullptr && root->right == nullptr) { //当前节点是叶子节点
                paths.push_back(path); //路径加入到答案中
            } else {
                path += "->"; //当前节点不是叶子节点，继续递归遍历
                construct_paths(root->left, path, paths);
                construct_paths(root->right, path, paths);
            }
        }
    }

    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> ans;
        construct_paths(root, "", ans);
        return ans;
    }
};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //广搜
    typedef struct {
        TreeNode *node;
        string val;
    } Node;
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> ans;
        queue<Node> que;

        que.push({root, to_string(root->val)});

        while (!que.empty()) {
            TreeNode *node = que.front().node;
            string path = que.front().val;
            que.pop();

            if (node->left == nullptr && node->right == nullptr) {
                ans.push_back(path);
            } else {
                if (node->left != nullptr) {
                    que.push({node->left, path + "->" + to_string(node->left->val)});
                } 
                if (node->right != nullptr) {
                    que.push({node->right, path + "->" + to_string(node->right->val)});
                }
            }
        }
        return ans;
    }
};

Leetcode 297.二叉树的序列化与反序列化

【思路】深搜，先序遍历得到先序序列，反序列化就根据先序序列得到一棵树。
【代码】官方题解

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Codec {
public:
    //深搜，先序遍历得到序列
    void rserialize(TreeNode *root, string &str) {
        if (root == nullptr) {
            str += "None,";
        } else {
            str += to_string(root->val) + ",";
            rserialize(root->left, str);
            rserialize(root->right, str);
        }
    }

    // Encodes a tree to a single string.
    string serialize(TreeNode* root) {
        string ret;
        rserialize(root, ret);
        return ret;
    }

    //根据"None"解析先序遍历的序列得到一棵树
    TreeNode *rdeserialize(list<string> &dataArray) {
        if (dataArray.front() == "None") {
            dataArray.erase(dataArray.begin());
            return nullptr;
        }
        TreeNode *root = new TreeNode(stoi(dataArray.front()));
        dataArray.erase(dataArray.begin());
        root->left = rdeserialize(dataArray);
        root->right = rdeserialize(dataArray);
        return root;
    } 

    // Decodes your encoded data to tree.
    TreeNode* deserialize(string data) {
        list<string> dataArray;
        string str;
        for (auto &ch: data) {
            if (ch == ',') {
                dataArray.push_back(str);
                str.clear();
            } else {
                str.push_back(ch);
            }
        }
        if (!str.empty()) {
            dataArray.push_back(str);
            str.clear();
        }
        return rdeserialize(dataArray);
    }
};

// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

【复杂度分析】

  • 时间复杂度： O ( n ) O(n) O(n)。序列化和反序列化函数中，每个节点只访问一次，因此时间复杂度是 O ( n ) O(n) O(n)，其中 n n n 为节点数，即树的大小。
  • 空间复杂度： O ( n ) O(n) O(n)。序列化和反序列化函数中，递归会用到栈空间，递归的深度即为空间复杂度，故渐进空间复杂度为 O ( n ) O(n) O(n)。
让二叉树更好——三叉树和线索二叉树（遍历的简化）
筱羊冰冰
08-03 2218
你是否已经厌倦了，那只能找到孩子却不能反向寻找双亲结点，那遍历起来想要砸键盘的、陈旧的二叉树？今天，就是我们站起来了的时候了。（雾） 好了不皮了，先看一下定义 三叉树 这个名字不是指度最大为三的树，而是在二叉树（两个指针）的基础上多了个指针，因为二叉树找双亲结点只能用栈存储然后回溯，或者只能一个个结点的寻找，非常麻烦的。 （别问名字为什么这样，问就是学校ppt教的，不过也很形象） 好处： 首先就是找到从根节点到任意节点的路径方便了很多； 另外是在非递归遍历的时候，之前的二叉树结构想要回溯就只能借助栈，而现在
数据结构~12.树与二叉树
热门推荐
qq_41424688的博客
08-04 3万+
数据结构学习~12.树 本文是上一篇文章的后续,详情点击该链接~ 树的基本概念        树是一种非线性的数据结构。要理解树的概念及其术语的含义,用一个例子说明是最好的方法。就比如下图就是一棵树,它是若干节点的集合。是由唯一的根(A)和若干互不相交的子树。就比如说,A,D,H,M,I,J这六个结点组成的树就是一颗子树组成的。其中,每一棵子树又是一棵树,也是由唯一的根结点和若干棵互不相交的子树组成的。由此而知,树的定义是递归的,也就是在
数据结构（三）树与二叉树基本概念
很注重数学和408
10-10 2320
树的基本概念 二叉树 树、森林 树与二叉树的应用
【C++】实现三叉树
Yinrtyu_的博客
02-09 278
在C++中，三叉树（每个节点有三个子节点）是一种特殊类型的树数据结构。每个节点包含一个数据元素以及三个指向其子节点的指针。这种数据结构可以应用于各种场景，比如决策树、多路搜索树等。
【常用数据结构——二叉树（还有三叉四叉...？ ）】
weixin_30394633的博客
08-13 1674
---恢复内容开始--- 简介 　　在计算机科学中，二叉树是每个结点最多有两个子树的有序树。通常子树的根被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用作二叉查找树和二叉堆或是二叉排序树。 基本术语　 子树：除了根节点外，每个子节点都可以分为多个不相交的子树。 孩子与双亲：若一个结点有子树，那么该结点称为子树根的"双亲"，...
数据结构与算法系列研究五——树、二叉树、三叉树、平衡排序二叉树AVL
weixin_30344995的博客
05-19 1145
树、二叉树、三叉树、平衡排序二叉树AVL 一、树的定义 树是计算机算法最重要的非线性结构。树中每个数据元素至多有一个直接前驱，但可以有多个直接后继。树是一种以分支关系定义的层次结构。 a.树是n(≥0)结点组成的有限集合。{N.沃恩} (树是n(n≥1)个结点组成的有限集合。{D.E.Knuth}) 在任意一棵非空树中： ⑴有且仅有一个没有前驱的结点...
数据结构之树
忆梦九洲的博客
01-25 1670
前面文章讲的线性表，不论数组还是链，都是“一对一”的关系，本文章节让我们来认识一下“一对多”关系的数据结构——树（Tree）。树结构分为二叉树和三叉树等，如下图所示。常用的就是二叉树，因此本节以二叉树为主要介绍对象，二叉树之外的树结构暂且统称为非二叉树。树在数据结构中占据重要的地位。对于树结构的学习其实不难，先了解它的概念和性质，然后结合图示去理解，最后亲自动手实现其功能，按照这样的思路去学习，一定可以轻松掌握。注意：一棵树的度，是树内各节点的度的最大值。
二叉树（数据结构作业）.rar_二叉树
09-19
二叉树是一种重要的数据结构，它在计算机科学中扮演着至关重要的角色，特别是在算法和数据存储方面。在本文中，我们将深入探讨二叉树的概念、性质、类型以及它们的应用。 二叉树的基本定义： 二叉树是每个节点最多...
NJUCM-数据结构课程6.实验六 二叉树的构建应用.zip
06-02
在NJUCM的数据结构课程中，实验六着重探讨了二叉树的构建及其应用。二叉树作为一种基础且重要的数据结构，在计算机科学中扮演着关键角色，尤其在算法设计和数据组织方面。在这个实验中，学生将深入理解二叉树的性质...
数据结构第五章-树与二叉树-C语言实现线索二叉树
03-16
【数据结构】第五章——树与二叉树——C语言实现线索二叉树 资源内包含7个文件： - 3个头文件 - BiTree.h ——二叉树头文件，用于对二叉树的数据结构的定义、实现算法的声明 - ThreadTree.h —— 线索二叉树头文件...
C语言/数据结构-树与二叉树-C语言实现树与森林的遍历
最新发布
03-19
【数据结构】第五章——树与二叉树——C语言实现树与二叉树 本资源中有三个文件： - <Tree.h>——树与森林遍历算法头文件 - <Tree.c>——树与森林遍历算法源文件 - <test.c>——树与森林遍历算法测试源文件 在本资源...
多叉树转二叉树
青竹梦
02-24 4022
将多叉树转为二叉树： #include #include #include #include using namespace std; struct list { int l; int r; }node[2001]; void init() { int i; scanf("%d%d",&n,&m); memset(vis,-1,sizeof(vis));
算法与数据结构——算法题 131：三叉树空指针（腾讯笔试题） ？ 待解决
wjheha的博客
12-18 1519
选择题：现有一个包含m个节点的三叉树，即每个节点都有三个指向孩子结点的指针，请问：在这3m个指针中有（）个空指针？ A、2m B、2m-1 C、2m+1 D、3m思路：
【数据结构】树
AAyyy1的博客
03-09 6093
【数据结构】-树树树的定义基本概念树的性质二叉树二叉树的定义及其主要性质二叉树的定义特殊的二叉树 树 树的定义 树是n（n≥0n\geq 0n≥0）个结点的有限集。当n=0时，称为空树。在任何一个非空树中应满足： 有且仅有一个特定的称为根的结点。 当n>1时，其余结点可分为m（m>0）个互不相交的有限集T1,T2,T3,…,Tm,其中每个集合又是一棵树，并且称为根的子树。 树是一种递归的数据结构。 具有以下两个特点： 树的根节点没有前驱，除根结点外的所有结点有且只有一个前驱。 树中的所有结
数据结构(3)：树与二叉树（上）-二叉树
kodoshinichi的博客
06-26 604
一.树的概念 (一)树的基本概念 树的定义 树是n个节点的有限集合（n≥0），当n=0的时候称为空树，在任意一棵非空树中： ①有且仅有一个特定的称为根的节点 ②当n＞1的时候，其余节点可分为m个互不相交的有限集合T1，…,Tm，每个 集合本身也是一棵树，并且这些集合称为根节点的子树。 特点： ①树的根节点没有前驱节点，除了根节点以外，所有节点有且只有一个前驱节点 ②树中所有节点都可以有0个或多个后继节点 ③在具有n个节点的树中具有n-1条边 基本术语 族谱关系（可以在树中找到连接两个
三叉树--北航
追梦少年ML的博客
07-06 1324
题目描述： 题目链接 Time Limit: 1000 ms Memory Limit: 256 mb 一个关于三叉树的题目，小于100的值代表树叶，大于100的值为分支点，建树的过程是水平方向建树， 输入格式： 先输入n，代表有n组数据，接下来n行，输入4个数，第一个数代表根节点，接下来分别代表三个子节点，-1代表子节点不存在，输入的顺序按照层次遍历的次序。接下来，要求寻找叶子节点的最短路径，最短路径是指不经过重复的边。输入方式，首先输入一个值m，代表m行，接下来m行输入m个叶子节点和对应的优先级，要求按
多叉树 转换为二叉树 算法
jasonkent27的专栏
09-23 6527
多叉树转换为二叉树算法。算法描述：将多叉树的第一个儿子结点作为二叉树的左结点，将其兄弟结点作为二叉树的右结点。 举例，如下图： 树的结构为： typedef struct BinaryTreeNode{ struct BinaryTreeNode* leftChild; struct BinaryTreeNode* rightChild; int value; }; typed
数据结构第五章：树
qq_43896405的博客
09-16 2265
文章目录树的基本概念常考性质二叉树1.基本概念2.几个特殊的二叉树3.二叉树常考性质4.完全二叉树的常考性质二叉树的存储结构1.顺序存储 树的基本概念 树是一种递归定义的数据结构 祖先结点、子孙结点、双亲结点（父节点）、孩子结点、兄弟结点、堂兄弟结点 有序树——逻辑上看，树中结点的各子树从左至右是有次序的，不能互换 无序树——逻辑上看，树中结点的各子树从左至右是无次序的，可以互换 森林：森林是m（m≥0）棵互不相交的树的集合 常考性质 根节点没算到总度数里 三叉树是每个结点最多三个孩子，可以没有
H.266/VVC中的四叉树+三叉树+二叉树(更新)
小小柴的博客
07-26 5661
        H.266已经确定采用混合树结构（MT），即由四叉树（QT），二叉树（BT）和三叉树（TT）结构组成。这种划分结构比之前非常灵活，极大的提高了编码性能。        CTU首先由四叉树结构划分，即CTU块可以不划分或递归地划分成4个相同大小的子块。然后，在QT的叶节点可以通过二叉树或三叉树结构进一步划分。二叉树和三叉树划分可以交错并递归进行。但是，一旦应用二叉树或三叉树划分，就...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值