欢迎使用CSDN-markdown编辑器

第1章 逻辑斯蒂回归

逻辑斯蒂回归模型

1.1.1 逻辑斯蒂分布

　　定义1.1 (逻辑斯蒂分布):设$X$是连续随机变量，$X$服从逻辑斯蒂分布是指$X$具有下列分布函数和密度函数：

$$F(x)=P(X \le x)=\frac{1}{1+e^{-(x-u)/r}}　　　　　　　(1.1)$$

$$f(x)=F'(x)=\frac{e^{-(x-u)/r}}{r(1+e^{-(x-u)/r})^2}　　　　　　　　(1.2)$$

其中，$u$为未知参数，$r$>0为形状参数
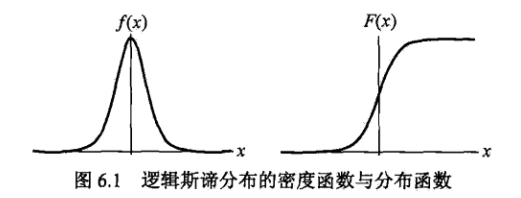
　　逻辑斯蒂分布的密度函数和分布函数如图6.1所示。分布函数属于逻辑斯蒂函数，其图形是一条$S$形曲(sigmoid curve)。该曲线以点($u$,$\frac{1}{2}$)为中心成对称，即满足

$$F(-x+u)-\frac{1}{2}=-F(x+u)+\frac{1}{2}$$

曲线在中心附近增长速度较快，在两端增长速度较慢。形状参数$r$的值越小，曲线在中心附近增长越快。
　　　　　　　　　

1.1.2 二项逻辑斯蒂回归模型

　　二项逻辑斯蒂回归模型是一种分类模型，由条件概率分布$P(X|Y)$表示，形式为参数化的逻辑斯蒂分布。其中，随机变量$X$取值为实数，随机变量$Y$取值为1或0,。我们通过监督学习的方法来估计模型参数。
　　定义1.2 (逻辑斯蒂回归模型)二项逻辑斯蒂回归模型是如下的条件概率分布：

$$P(Y=1|X)=\frac{e^{w*x+b}}{1+e^{w*x+b}}　　　　　　　　　(1.3)$$

$$P(Y=0|X)=\frac{1}{1+e^{w*x+b}}　　　　　　　　　(1.4)$$

其中，$x\in R^n$是输入，$Y \in \{0,1\}$是输出，$w \in R^n$和$b\in R$是参数，$w$称为权重，$b$称为偏置，$w*x$是$w$和$x$的内积。
　　对于给定输入$x$，计算$P(Y=1|X)$，$P(Y=0|X)$。比较两者大小，将实例$x$分到概率值大的那一类。
　　有时为了方便，将权重向量和输入向量加以扩充，即$w=(w_1,w_2,w_3,...,w_n,b)^T$，$x=(x_1,x_2,x_3,...,x_n,1)^T$。注意，这里$x \in R^{n+1}$,$w \in R^{n+1}$此时逻辑斯蒂回归模型扩展如下：

$$P(Y=1|X)=\frac{e^{w*x}}{1+e^{w*x}}　　　　　　　　　　　(1.5)$$

$$P(Y=0|X)=\frac{1}{1+e^{w*x}}　　　　　　　　　　　(1.6)$$

　　现在考察逻辑斯蒂回归模型的特点。一个事件的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值。如果事件发生的概率是 $p$，那么该事件的几率是$\frac{p}{1-p}$，该事件的对数几率(log odds)或logit函数是：

$$logit(p)=log\frac{p}{1-p}$$

对于逻辑斯蒂回归而言，由式(1.5)和式(1.6)得：

$$log \frac{P(Y=1|X)}{1-P(Y=1|X)}=w*x$$

也就是说，在逻辑斯蒂回归模型中，输出$Y=1$的对数几率是输入$x$的线性函数。

1.3 模型参数估计

　　逻辑斯蒂回归模型学习时，对于给定的训练集$T=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}$，其中，$x_i \in R^n$，$Y\in \{0,1\}$，可以用极大似然估计来估计参数，从而得到回归模型。
　　设：$P(Y=1|x)=\pi(x)$，$P(Y=0|x)=1-\pi(x)$
则似然函数为：$\prod_{i=1}^{N}[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}$
对数似然函数为：

$$L(w)=\sum_{i=1}^{N}[y_ilog\pi(x_i)+(1-y_i)log(1-\pi(x_i))]$$

$$=\sum_{i=1}^{N}[y_ilog{\frac {\pi(x_i)}{1-\pi(x_i)}}+log(1-\pi(x_i))]$$

$$=\sum_{i=1}^{N}[y_i(wx_i)-log(1+e^{wx_i})]$$

对$L(w)$求极大值，得到 w <script type="math/tex" id="MathJax-Element-190">w</script>的估计值。
　　这样，问题就变成以对数似然函数为目标函数的最优化问题。逻辑斯蒂回归学习中通常采用的方法是梯度下降及拟牛顿法。
　　1、求解方法一：梯度上升法