Codeforces #24 C. Sequence of points

C. Sequence of points

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given the following points with integer coordinates on the plane:M₀, A₀, A₁, ..., A_n - 1, wheren is odd number. Now we define the following infinite sequence of pointsM_i:M_i is symmetric toM_i - 1 according (for every natural numberi). Here point B is symmetric toA according M, ifM is the center of the line segment AB. Given index j find the pointM_j.

Input

On the first line you will be given an integer n (1 ≤ n ≤ 10⁵), which will be odd, andj (1 ≤ j ≤ 10¹⁸), wherej is the index of the desired point. The next line contains two space separated integers, the coordinates ofM₀. After thatn lines follow, where the i-th line contain the space separated integer coordinates of the pointA_i - 1. The absolute values of all input coordinates will not be greater then1000.

Output

On a single line output the coordinates of M_j, space separated.

Sample test(s)

Input

3 4
0 0
1 1
2 3
-5 3

Output

14 0

Input

3 1
5 5
1000 1000
-1000 1000
3 100

Output

1995 1995

小伙伴为了明天的轻工校赛而找的比赛题目，一共三题，难度好像都不小啊。。。

这个题题意比较难理解，就是给出n,j；之后再给出m[0]的坐标，a[0]-a[n-1]的坐标

让你输出m[j]的坐标,其中m[i]和m[i-1]关于a[(i-1)%n]对称

因为j最大为10的18次方，所以想到找规律。。。

我就把两个样例的m[1]-m[6]都列出来，结果发现m[6]和m[1]重合了！！！

就是说m[i%(2*n)]==m[i]

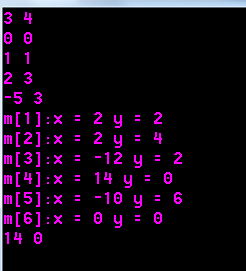
代码如下：

#include <map>
#include <cmath>
#include <vector>
#include <string>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define esp 1e-9
#define MAXN 200010
#define ll long long
#define INF 0x7FFFFFFF
#define BUG system("pause")
#define SW(a,b) a^=b;b^=a;a^=b;
using namespace std;
struct Point{
	int x, y;
}m[MAXN], a[MAXN];
int main(void){
	int n;
	ll  j;
	while(cin >> n >> j) {
		cin >> m[0].x >> m[0].y;
		for(int i=0; i<n; ++i){
			cin >> a[i].x >> a[i].y;
		}
		for(int i=0; i<2*n; ++i){
			m[i+1].x = 2*a[i%n].x-m[i].x;
			m[i+1].y = 2*a[i%n].y-m[i].y;
			cout << "m[" << i+1 << "]:x = " << m[i+1].x << " y = " << m[i+1].y << endl;
		}
		cout << m[j%(2*n)].x << " " << m[j%(2*n)].y << endl;
	} 

	return 0;
}