C++算法入门练习——约数个数

最新推荐文章于 2025-04-02 15:46:08 发布

原创最新推荐文章于 2025-04-02 15:46:08 发布 · 2.1k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #数据结构

文章介绍了如何使用素数表和组合数的原理来优化计算给定正整数的约数个数，对比了直接模拟的方法，并提供了C++代码实现。

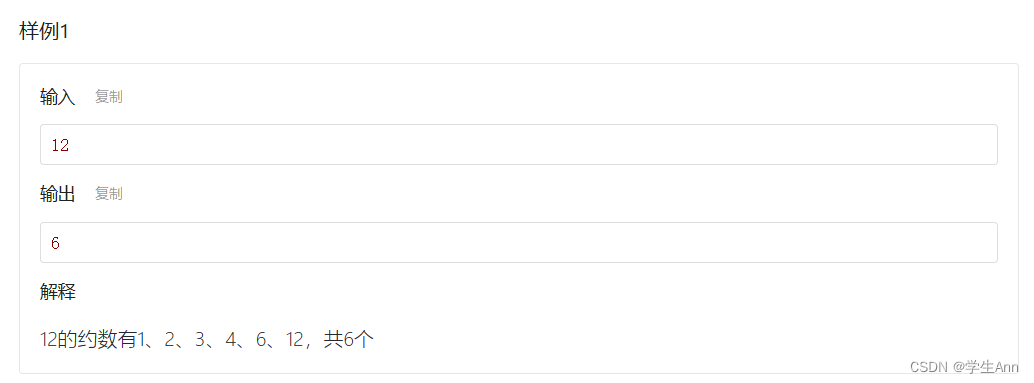
给定一个正整数n，求n的约数个数。

解题思路：

我们当然可以直接去模拟，从1到n去计算一遍，进行统计约数的个数。

代码如下：

#include <iostream>
using namespace std;

int main(){
	int n;
	cin>>n;
	int count = 0;
	for(int i=1;i<=n;i++){
		if(n%i==0){
			count++;
		}
	}
	cout<<count<<endl;
	return 0;
}

但同时我们也还可以换一个思路，我们如何去优化找约数？

我们可以利用素数表。

例如，12的质因数为：2（2个），3（1个）。

而12的约数组成是：1，2，4，3，6，12。

从这个例子可以看出一个规律：约数的和 = 1 + 从小开始的组合数。

上述例子表示为： 1 + 2 + 3*1

代码形式为：result = 1；

result += result * count[i]

完整代码如下：

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;

vector<int> primes;
bool isprime[10000001];

void find_primes(int n){
	memset(isprime,true,sizeof(isprime));
	for(int i=2;i<=n;i++){
		if(isprime){
			primes.push_back(i);
			for(int j=i+i;j<=n;j+=i){
				isprime[j] = false;
			}
		}
	}
}

struct factor{
	int num;
	int count = 0;
};

int main(){
	int n;
	cin>>n;
	bool flag[n];
	int count = 1;
	vector<factor> fac;
	find_primes(n);
	for(int i=0;;i++){
		bool flag = false;
		factor temp;
		if(primes[i]>n||n==1){
			break;
		}
		if(n%primes[i]==0){
			temp.num = primes[i];
			flag = true;
		}
		while(n%primes[i]==0){
			temp.count++;
			n /= primes[i];
		}
		if(flag){
			fac.push_back(temp);
		}
	}
	count += count * fac[0].count;
	for(int i=1;i<fac.size();i++){
		int temp = count;
		temp *= fac[i].count;
		count+=temp;
	}
	cout<<count<<endl;
	return 0;
}