一个简单的分治算法求矩阵相乘
C=A * B ,假设三个矩阵均为n×n,n为2的幂。可以对其分解为4个n/2×n/2的子矩阵分别递归求解:
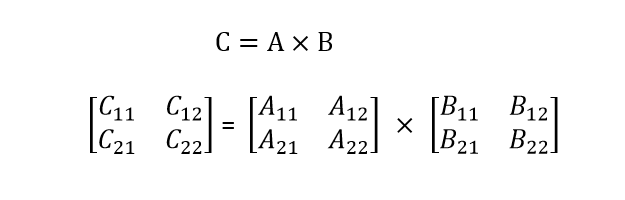
递归分治算法:
算法中一个重要的细节就是在分块的时候,采用的是下标的方式。
#include <stdio.h>
#include <stdlib.h>
#define ROW 16 //指定 行数
#define COL 16 //指定 列数
int a[ROW][COL],b[ROW][COL]; //矩阵a 和 矩阵b
int **c; // c = a * b
//保存一个矩阵的第一个元素的位置,即左上角元素的下标
//如果加上一个长度就可以知道整个矩阵了
typedef struct { //这里没有指定一个矩阵的长度,在分块时应该加入长度,否则不知道子块矩阵的大小
int str,stc; //str行下标 ; strc列下标
}subarr;
// 两矩阵arr、brr相加减 保存在temp中
void operate(int **arr,int **brr,subarr te,char op,int **temp,int len);
//分治法 求矩阵相乘 ,sa,sb分别为矩阵a,b参加运算的首元素
int ** square_recursive(subarr sa,subarr sb,subarr sc,int len){
int n=len;
int **temp;
int i;
// 申请一个临时矩阵,用于保存a*b
temp=(int**)malloc(sizeof(int *)*n);
for ( i=0;i<n;++i){
temp[i]=(int *)malloc(sizeof(int)*n);
}
// 长度为1 则直接相乘
if (n==1)
{
temp[0][0]=a[sa.str][sa.stc]*b[sb.str][sb.stc];
}else{
// 这里都是对下标进行初始化
// sa,sb,sc代表输入矩阵A,B,temp参加运算的首元素下标,因为进行分块后只进行特定子块的运算
//标号1,2,3,4 分别代表第一、二、三、四个子块
subarr sa1,sb1, sc1;
subarr sa2,sb2, sc2;
subarr sa3, sb3,sc3;
subarr sa4, sb4, sc4;
// 矩阵A 进行分块后的各个子块下标
sa1.str=sa.str;
sa1.stc=sa.stc;
sa2.str=sa.str;
sa2.stc=sa.stc+n/2;
sa3.stc=sa.stc;
sa3.str=sa.str+n/2;
sa4.str=sa.str+n/2;
sa4.stc=sa.stc+n/2;
// 矩阵B 进行分块后的各个子块下标
sb1.str=sb.str;
sb1.stc=sb.stc;
sb2.str=sb.str;
sb2.stc=sb.stc+n/2;
sb3.stc=sb.stc;
sb3.str=sb.str+n/2;
sb4.str=sb.str+n/2;
sb4.stc=sb.stc+n/2;
// 矩阵temp 进行分块后的各个子块下标
sc1.str=sc1.stc=0;
sc2.str=0;
sc2.stc=n/2;
sc3.stc=0;
sc3.str=n/2;
sc4.str=n/2;
sc4.stc=n/2;
// 将矩阵分为四块 分别求解。采用下标的方式进行分块,可以省去复制矩阵所产生的时间
// 若要复制矩阵则会产生 O(n*n)的时间复杂度
operate(square_recursive(sa1,sb1,sc1,n/2),square_recursive(sa2,sb3,sc1,n/2),sc1,'+',temp,n/2);
operate(square_recursive(sa1,sb2,sc2,n/2),square_recursive(sa2,sb4,sc2,n/2),sc2,'+',temp,n/2);
operate(square_recursive(sa3,sb1,sc3,n/2),square_recursive(sa4,sb3,sc3,n/2),sc3,'+',temp,n/2);
operate(square_recursive(sa3,sb2,sc4,n/2),square_recursive(sa4,sb4,sc4,n/2),sc4,'+',temp,n/2);
}
return temp;
}
// temp矩阵的te位置(四个子块中的一个)=arr+brr
// len表示arr,brr参加运算的长度
// op是运算符 ‘+’
void operate(int **arr,int **brr,subarr te,char op,int **temp,int len){
int i,j;
switch(op){
case '+':
for (i=0;i<len;++i){
for (j = 0; j < len; ++j)
{
temp[te.str+i][te.stc+j]=arr[i][j]+brr[i][j];
}
}
break;
case '-':
for (i=0;i<len;++i){
for (j = 0; j < len; ++j)
{
temp[te.str+i][te.stc+j]=arr[i][j]-brr[i][j];
}
}
break;
}
}
//为矩阵初始化 即赋值
void createarr(int temp[][COL]){
int i,j;
for (i = 0; i < ROW; ++i)
{
for (j = 0; j < COL; ++j)
{
temp[i][j]=(int)rand()%5;
}
}
}
// 打印C矩阵
void print(){
int i,j;
printf("\n====================================\n");
for (i = 0; i < ROW; ++i)
{
for (j = 0; j < COL; ++j)
{
printf("%d\t", c[i][j]);
}
printf("\n");
}
printf("===================================\n");
}
// 打印矩阵
void printarray(int a[ROW][COL]){
int i,j;
printf("-----------------------\n");
for (i = 0; i < ROW; ++i)
{
for (j = 0; j < COL; ++j)
{
printf("%d \t", a[i][j]);
}
printf("\n");
}
printf("-----------------------\n");
}
int main(){
int i,j;
subarr sa,sb,sc;
int len;
//初始化各个下标
sa.str=sa.stc=0;
sb.str=sb.stc=0;
sc.str=sc.stc=0;
// 长度赋值,因为在subarr结构里没有长度的定义
len=ROW;
//申请空间
c=(int**)malloc(sizeof(int *)*len);
for (i=0;i<len;++i){
c[i]=(int *)malloc(sizeof(int)*len);
}
// 给矩阵A,B 复制初始化
createarr(a);
createarr(b);
// 进行运算
c=square_recursive(sa,sb,sc,len);
// 打印矩阵A,B,C
printarray(a);
printarray(b);
print();
return 0;
}
=========== 王杰 原创作品转载请注明出处==============























 8153
8153











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








