点击上方“AI公园”,关注公众号,选择加“星标“或“置顶”
导读作者:Vardan Grigoryan
编译:ronghuaiyang
知识图谱是AI领域非常有用的一种工具,知识图谱的基础就是图论,从今天开始,给大家介绍一些图论的基础内容,今天是第一篇,哥尼斯堡七桥问题与欧拉图。
让我们从我经常在图论书中遇到的一些东西开始,这些书讨论了“图论的起源”,即哥尼斯堡7桥。Kaliningrad有七座桥,连接着被Pregolya河环绕的两个大岛和被同一条河分割的大陆的两部分。
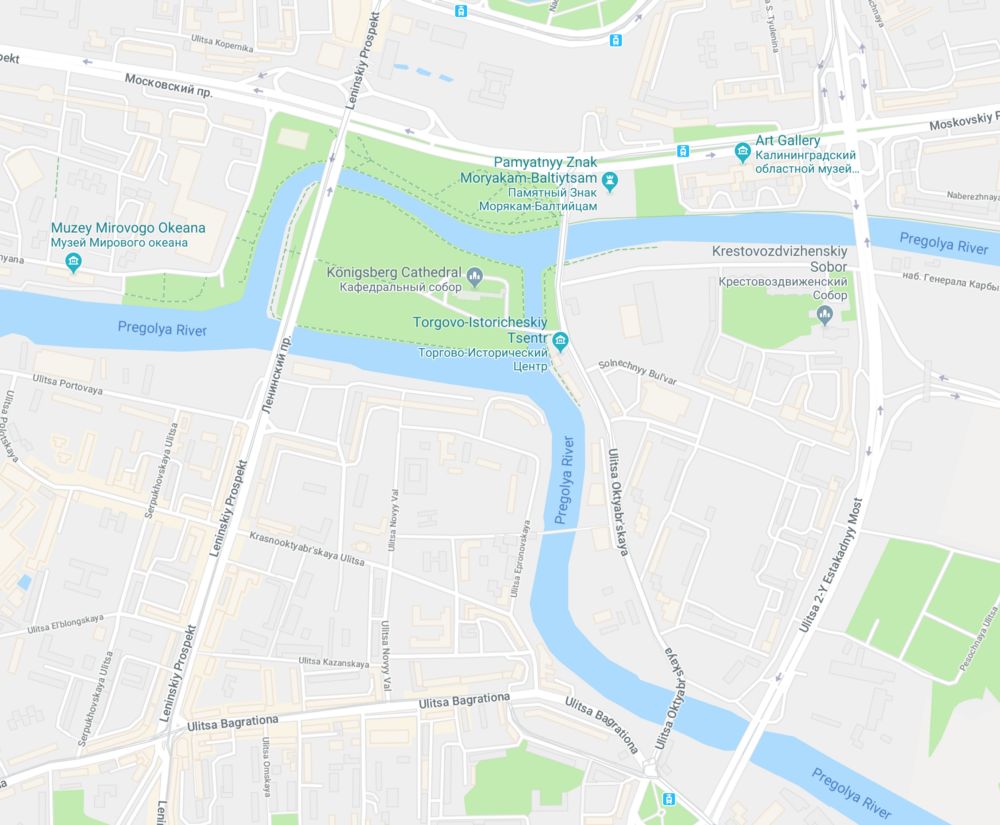
在18世纪,这里被称为哥尼斯堡(普鲁士的一部分),上面有更多的桥梁。这个问题,或者只是一个脑筋急转弯,穿过哥尼斯堡的每个桥梁只需要一次就可以穿过这个城市。当时他们没有互联网,所以这个事情应该很有趣。这是18世纪哥尼斯堡七座桥的图片。
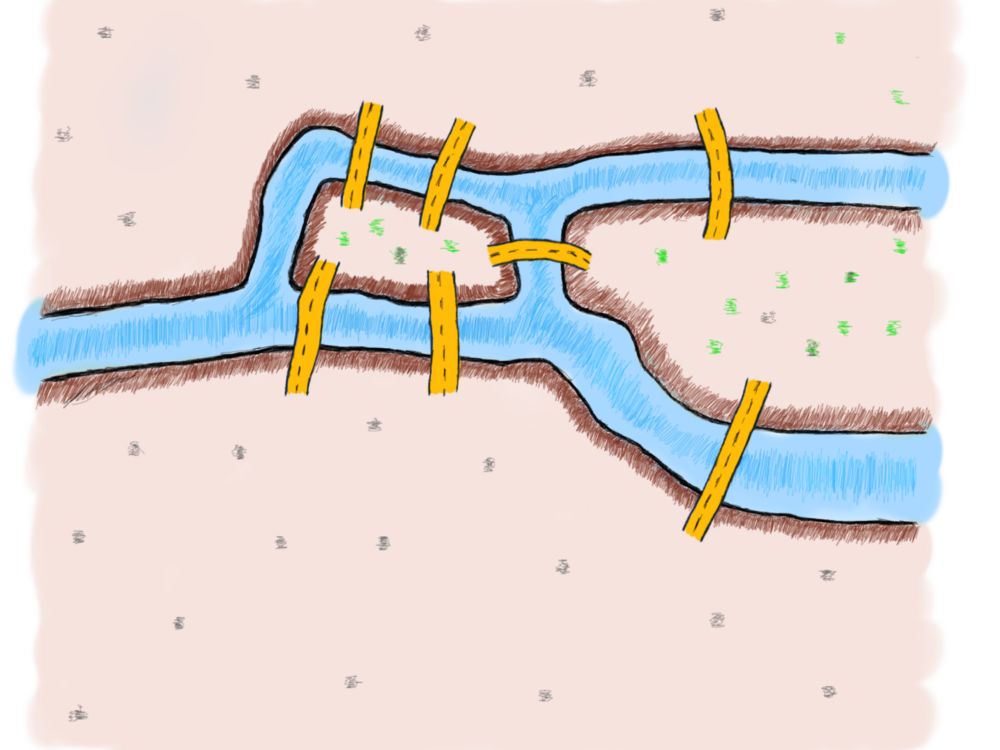
试一试。看看你是否可以通过每座桥只过一次就能穿过这座城市。
不能有任何未跨越的桥梁。
每座桥不得跨越超过一次。
如果你熟悉这个问题,你就知道它是不可能做到的。虽然你已经很努力了,你可能会更加努力,你最终会放弃。

有时候快速放弃是合理的。欧拉就是这样解决这个问题的——他很快就放弃了。他没有试图去解决这个问题,而是采用了一种不同的方法,试图证明不可能通过一次又一次地通过每一座桥来穿过这座城市。
让我们试着理解欧拉是如何思考的,以及他是如何提出解决方案的(如果没有解决方案,它仍然需要一个证明)。这是一个真正的挑战,因为走在这样一位德高望重的数学家的思维过程中是不光彩的。我们宁愿假装“像欧拉那样思考”。让我们从想象不可能的事情开始。
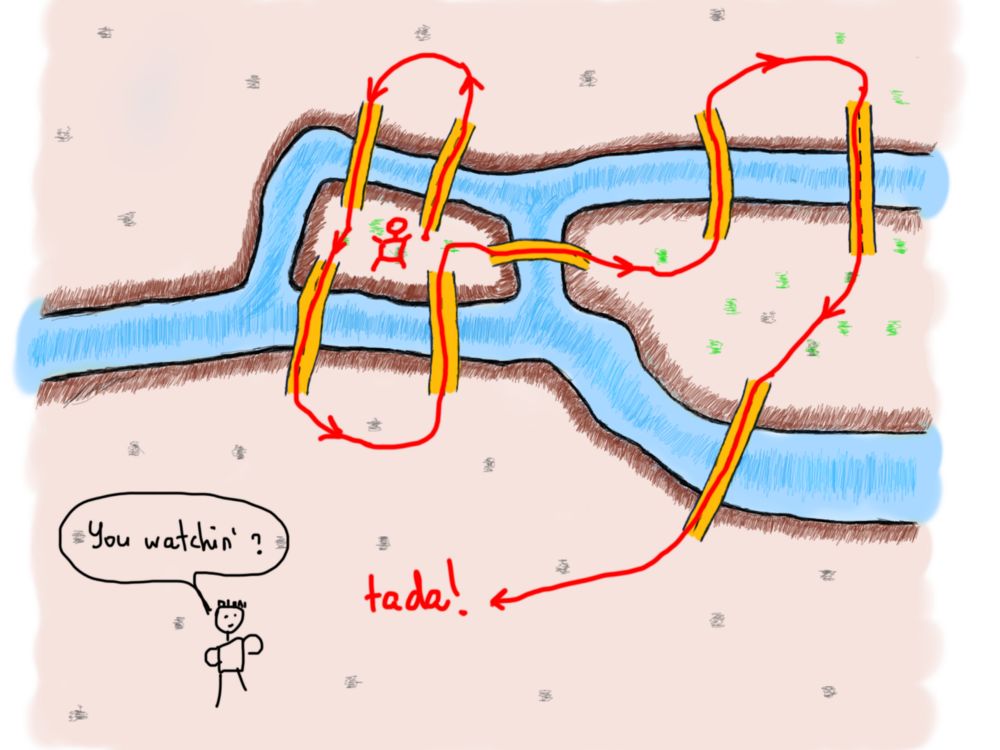
有四个不同的地方,两个岛屿和大陆的两个部分。和七个桥梁。有趣的是,我们将发现连接岛屿或大陆的桥梁数量是否存在某种模式(我们将使用术语“陆地”来指代这四个不同的地方)。
乍一看,似乎存在某种模式。每片土地上都有奇数座桥相连。如果你必须穿过每一座桥一次,那么你可以进入一块土地,如果它有两座桥,你可以离开它。


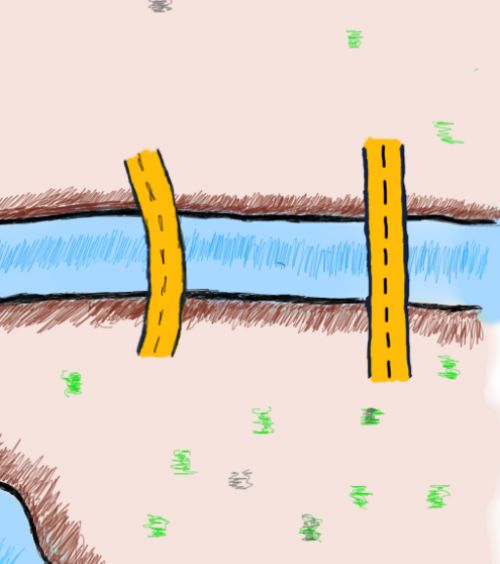
从上面的插图中很容易看出,如果你通过一座桥进入一块土地,你总是可以通过第二座桥离开这块土地。当第三座桥出现的时候,一旦你通过所有的桥进入这块土地,你就不能离开它。如果你试着把这个推理推广到一块土地上,你会发现,在偶数座桥的情况下总是有可能离开这片土地的,而在奇数座桥的情况下就不是这样了。在你的脑海里试试!
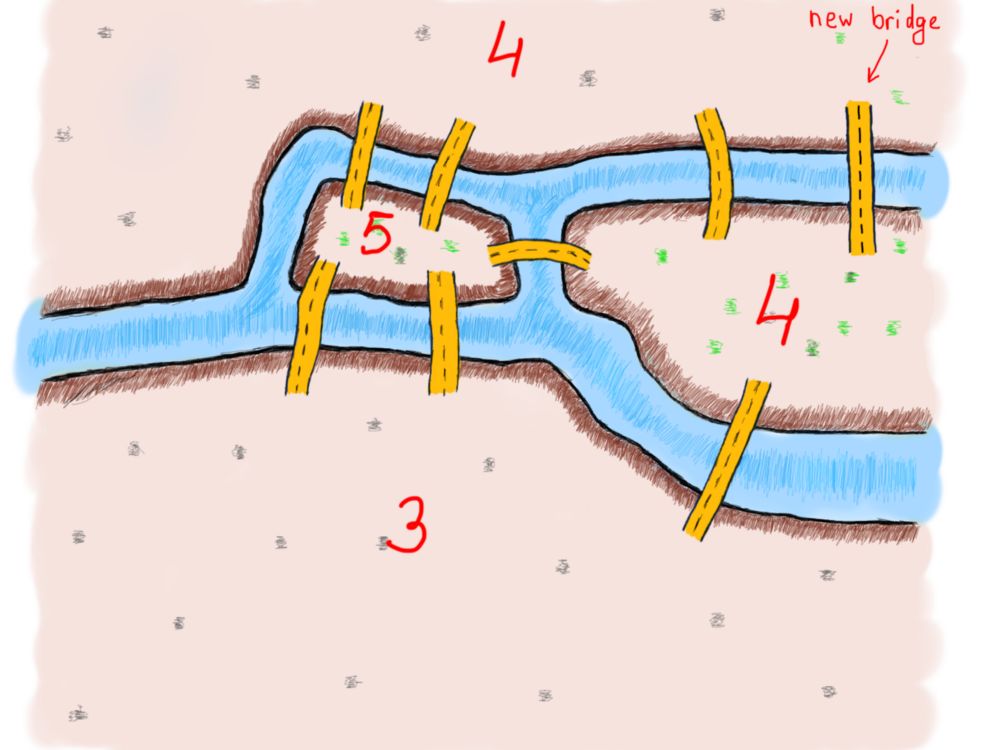
让我们添加一个新的桥,以查看总体连接桥的数量如何变化,以及它是否解决了这个问题。
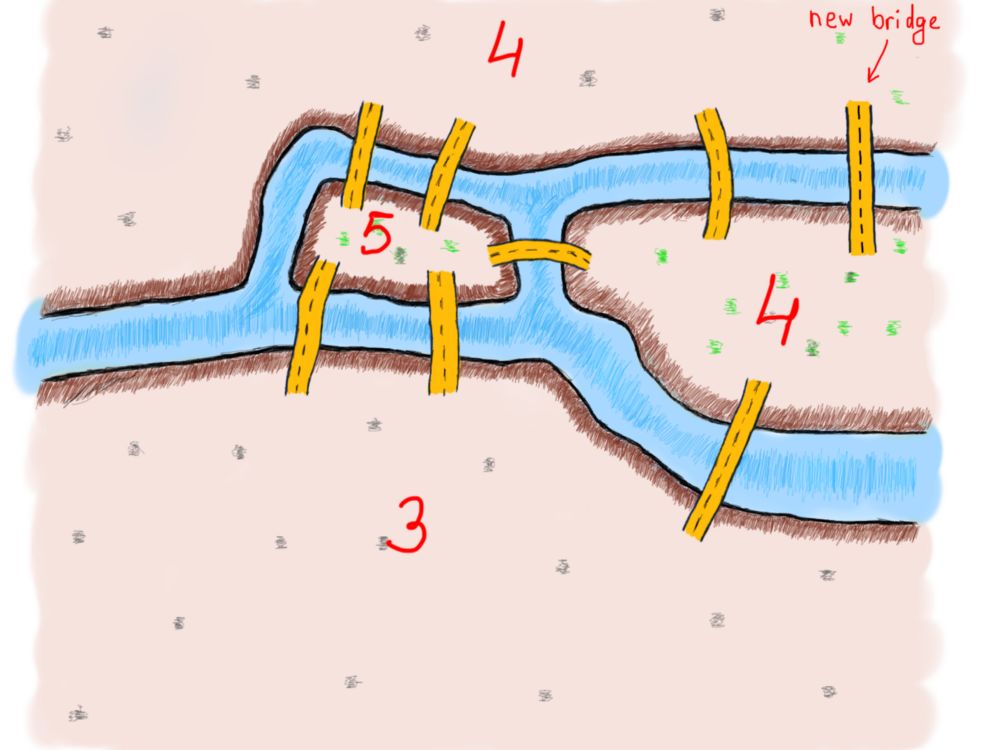
现在我们有两个偶数(4和4)和两个奇数(3和5)的桥梁连接这片土地,让我们画一个新的路线,加上这个新的桥梁。

我们看到偶数和奇数桥的数量在决定解决方案是否可行方面发挥了作用。这是一个问题。桥梁的数量是否解决了这个问题?应该一直是这样吗?事实证明并非如此。欧拉就是这么做的。他找到了一种方法来证明桥梁的数量很重要。更有趣的是,拥有奇数个连接桥梁的土地的数量也很重要。这就是欧拉开始将土地和桥梁“转换”成我们所知的图形的时候。下面是表示哥尼斯堡桥问题的图(注意,我们“临时”添加的桥不在其中)。
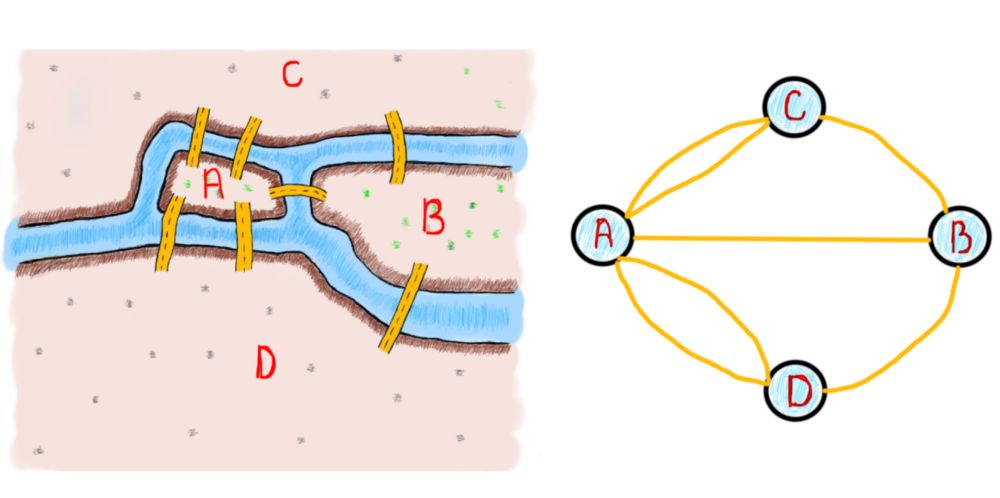
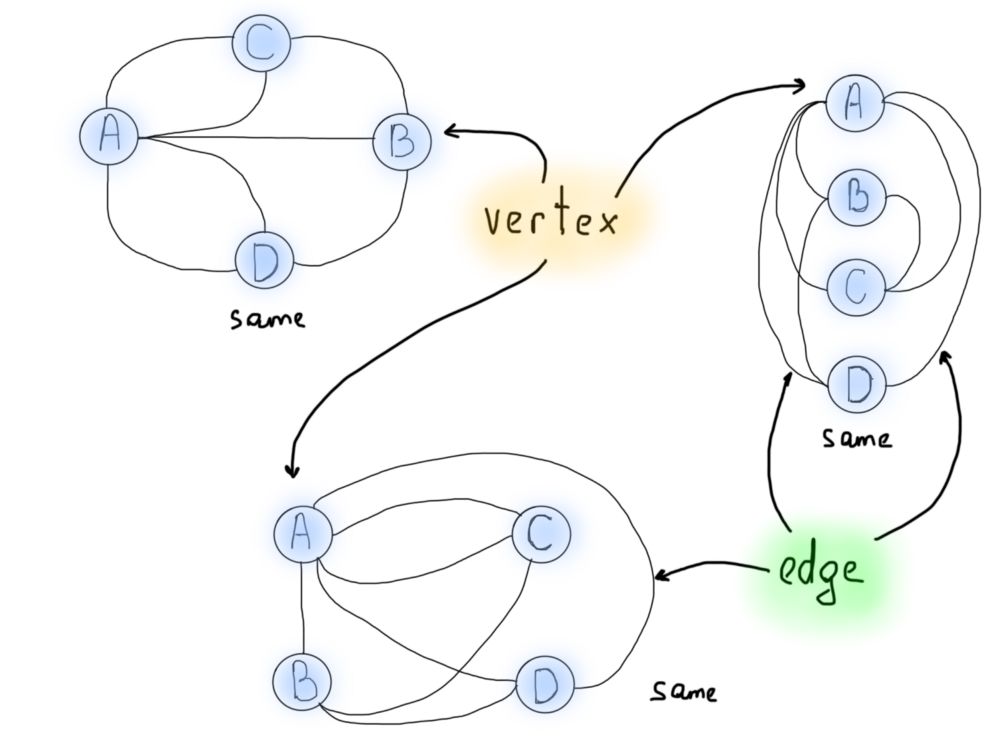
需要注意的一件重要事情是问题的泛化/抽象。每当你解决一个特定的问题时,最重要的是对类似问题的解决方案进行概括。在这个特殊的例子中,欧拉的任务是将桥梁穿越问题推广到未来能够解决类似的问题,即世界上所有的桥梁。可视化还有助于从不同的角度看待问题。下面的图都是上面所示的同一个哥尼斯堡问题的各种表示。
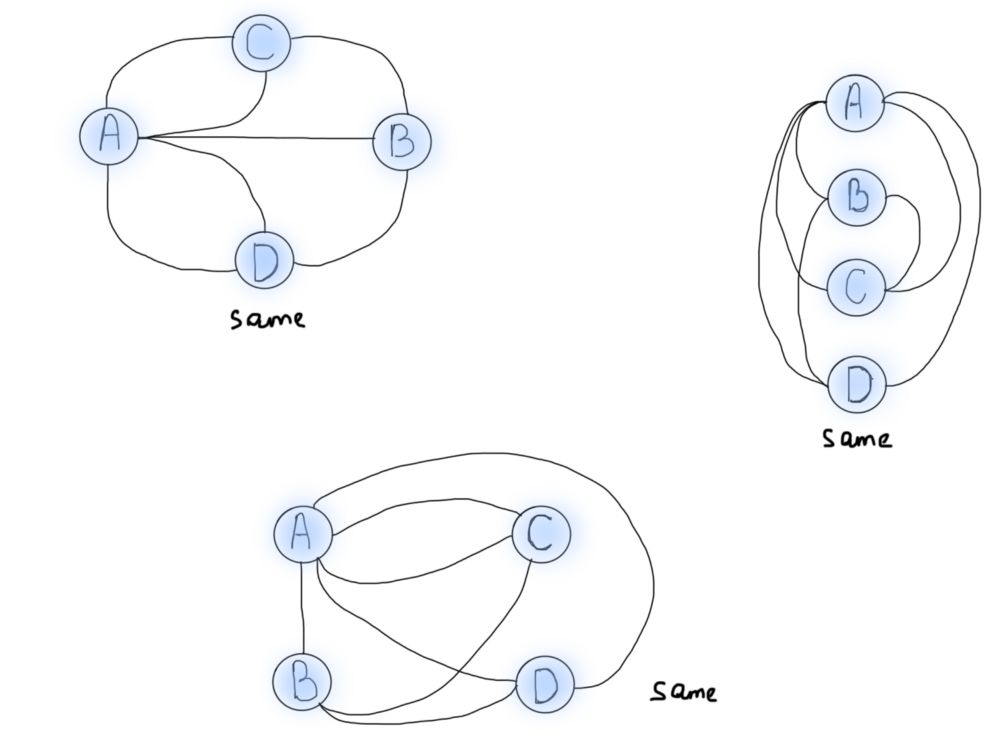
所以,图形是描绘问题的好方法。但是现在我们需要找出如何使用图来解决Konigsberg问题。注意从每个圆出来的线的数量。我们给它们命名一下,从现在开始,我们将把圆称为顶点,连接它们的线称为边。你可能见过字母符号,V表示顶点,E表示边。
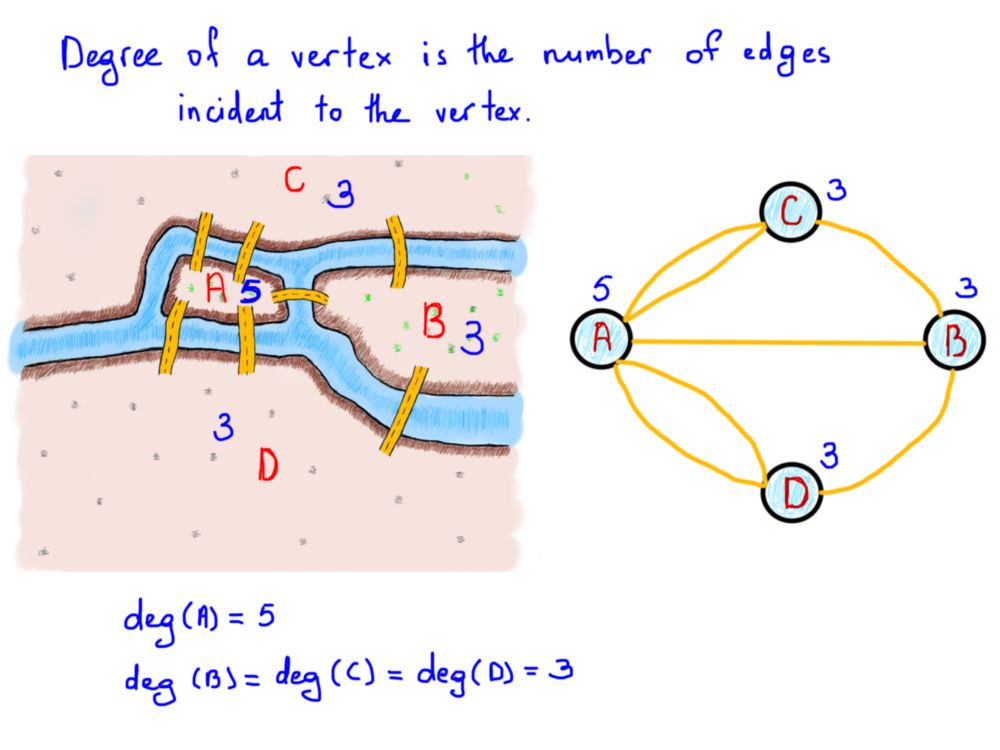
下一个重要的东西是所谓的顶点的度,连接到该顶点的边的数量。在上面的例子中,连接到土地的桥的数量可以表示为图顶点的度数。
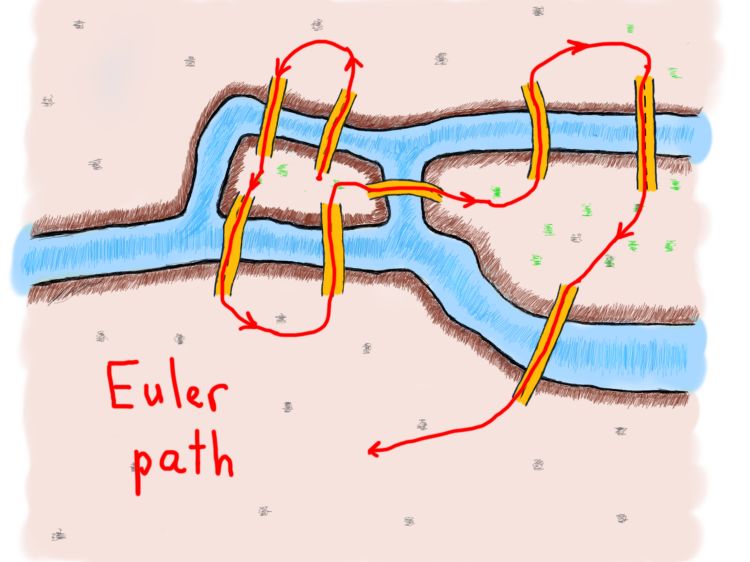
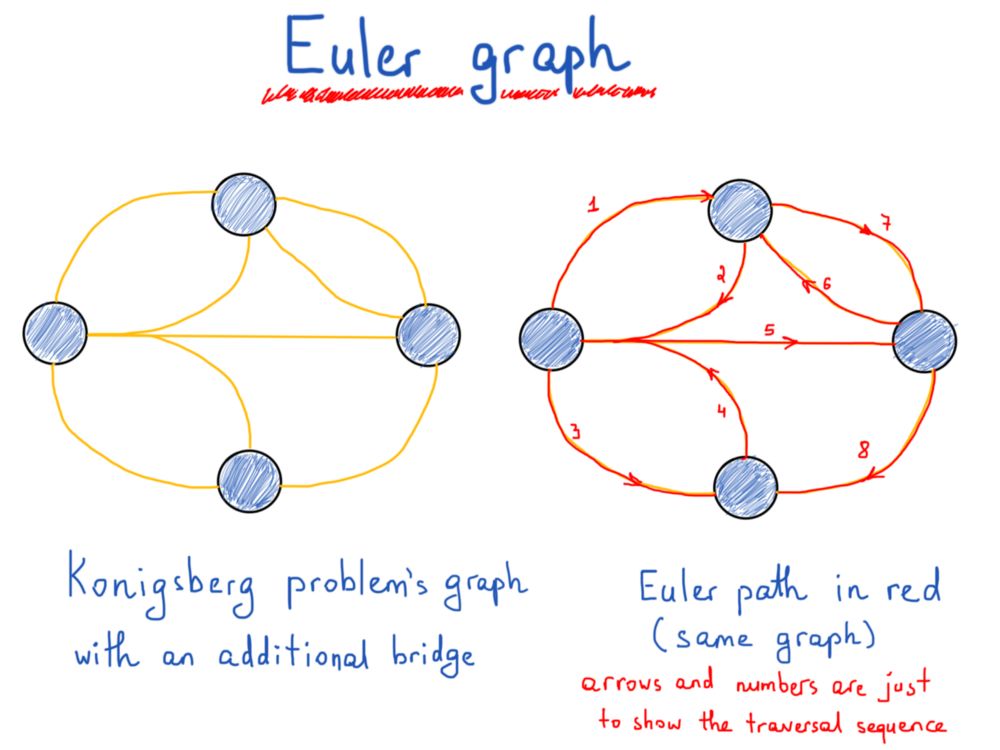
欧拉在他的努力中表明,遍历图(城市)一次且仅一次遍历每条边(桥梁)的可能性严格依赖于顶点(土地)的度数。由这些边组成的路径称为欧拉路径。欧拉路径的长度是边的数量。做好准备迎接一些严格的语言。?
有限无向图G(V, E)的欧拉路径是这样一条路径,使得G的每条边都只出现一次。如果G有一个欧拉路径,那么它就叫做欧拉图。
定理 一个有限无向连通图是一个欧拉图,当且仅当恰好有两个顶点是奇数度或所有顶点都是偶数度。在后一种情况下,图的每条欧拉路径都是一个回路,而在前一种情况下,没有一条是回路。
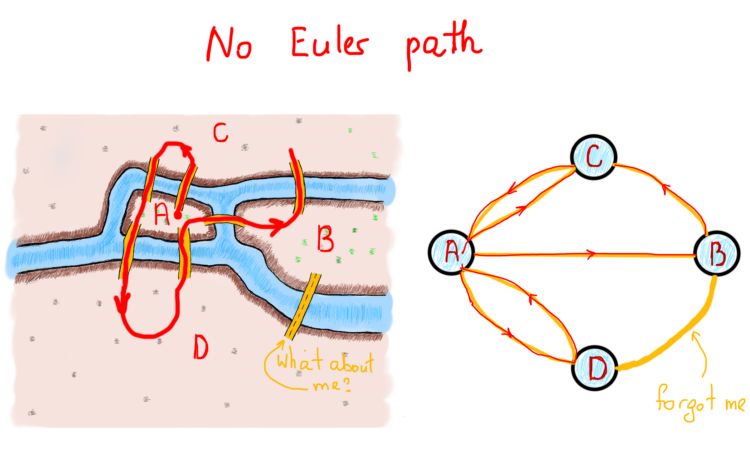
首先,让我们说明一下上述定义和定理中的新术语。
无向图 -边没有特定方向的图。
有向图 -边有特定方向的图。
连通图 -没有不可达顶点的图。每一对顶点之间必须有一条路径。
不连通的图 -具有不可到达顶点的图。并不是每一对顶点之间都有一条路径。
有限图 -具有有限数量节点和边的图。
无限图 -图的某一特定方向上的端点延伸到无穷远处的图。
我们将在接下来的段落中讨论其中的一些术语。
图可以有向也可以无向,这是图的一个有趣的性质。你一定见过一个流行的Facebook vs. Twitter的定向图和无定向图的例子。Facebook上的友谊关系可以很容易地表示为无向图,因为如果Alice是Bob的朋友,那么Bob也一定是Alice的朋友。没有方向,彼此都是朋友。
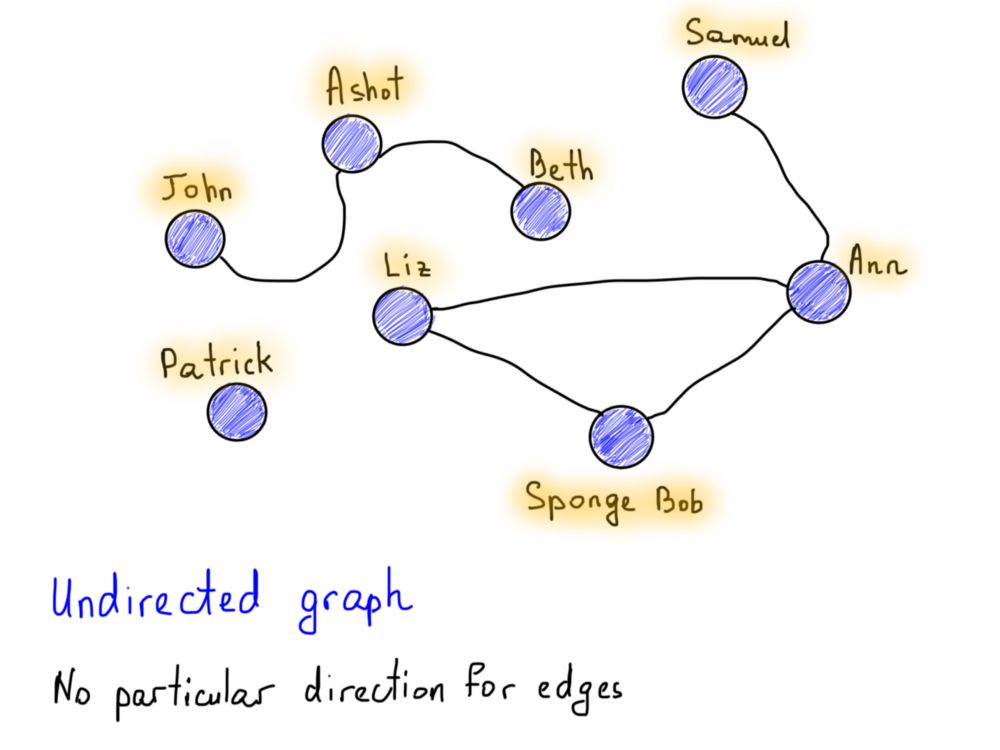
还要注意标记为“Patrick”的顶点,它有点特殊(他没有朋友),因为它没有任何关联边。它仍然是图的一部分,但在本例中,我们将说这个图是不连通的,它是一个不连通的图(“John”、“Ashot”和“Beth”也是如此,因为它们相互连接,但彼此分离)。在连通的图中没有不可达的顶点,每对顶点之间必须有一个路径。
与Facebook的例子相反,如果Alice在Twitter上关注Bob,这并不要求Bob关注Alice。因此,“follow”关系必须有一个方向指示器,显示哪个顶点(用户)具有指向另一个顶点的边(follow)。
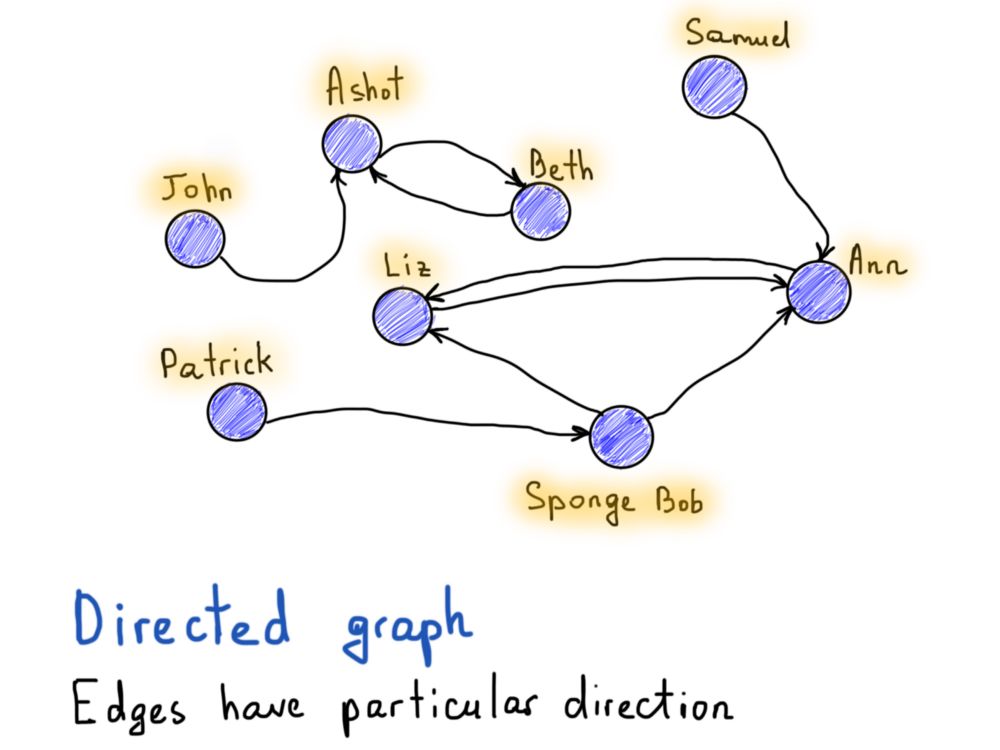
现在,知道了什么是有限连通无向图,让我们回到欧拉图:
那么,我们为什么要首先讨论Königsberg桥问题和欧拉图呢?它不是那么枯燥,通过研究这个问题和前面的解决方案,我们接触了图背后的元素(顶点、边、有向、无向),避免了枯燥的理论方法。不,我们还没有做完欧拉图和上面的问题。?
现在我们应该继续讨论图的计算机表示,因为这是我们程序员感兴趣的主题。通过在计算机程序中表示图形,我们将能够设计一种跟踪图形路径的算法,从而确定它是否是欧拉路径。在此之前,尝试一下为欧拉图想出一个好的应用(除了摆弄桥之外)。
(未完待续)
 —
END—
—
END—
英文原文:https://medium.com/free-code-camp/i-dont-understand-graph-theory-1c96572a1401

请长按或扫描二维码关注本公众号
喜欢的话,请给我个好看吧!![]()























 5586
5586

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








