判断一棵二叉树是否为平衡二叉树

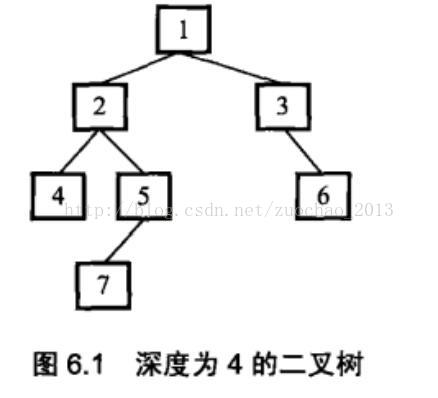
   问题:输入一棵二叉树的根结点，判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。例如下面就是一棵平衡二叉树。

运用递归自底向上(从叶子结点到根结点)的思想实现的代码:

// ====================方法1(自根到叶子)====================
int TreeDepth(BinaryTreeNode* pRoot)
{
    if(pRoot == NULL)
        return 0;

    int nLeft = TreeDepth(pRoot->m_pLeft);
    int nRight = TreeDepth(pRoot->m_pRight);

    return (nLeft > nRight) ? (nLeft + 1) : (nRight + 1);
}

bool IsBalanced_Solution1(BinaryTreeNode* pRoot)
{
    if(pRoot == NULL)
        return true;

    int left = TreeDepth(pRoot->m_pLeft);
    int right = TreeDepth(pRoot->m_pRight);
    int diff = left - right;
    if(diff > 1 || diff < -1)
        return false;

    return IsBalanced_Solution1(pRoot->m_pLeft) 
        && IsBalanced_Solution1(pRoot->m_pRight);
}

// ====================方法2(自叶子到根)====================
bool IsBalanced(BinaryTreeNode* pRoot, int* pDepth);

bool IsBalanced_Solution2(BinaryTreeNode* pRoot)
{
    int depth = 0;
    return IsBalanced(pRoot, &depth);
}

bool IsBalanced(BinaryTreeNode* pRoot, int* pDepth)
{
    if(pRoot == NULL)
    {
        *pDepth = 0;
        return true;
    }

    int left, right;
    if(IsBalanced(pRoot->m_pLeft, &left) 
        && IsBalanced(pRoot->m_pRight, &right))
    {
        int diff = left - right;
        if(diff <= 1 && diff >= -1)
        {
            *pDepth = 1 + (left > right ? left : right);
            return true;
        }
    }

    return false;
}

// ====================测试代码====================
void Test(char* testName, BinaryTreeNode* pRoot, bool expected)
{
    if(testName != NULL)
        printf("%s begins:\n", testName);

    printf("Solution1 begins: ");
    if(IsBalanced_Solution1(pRoot) == expected)
        printf("Passed.\n");
    else
        printf("Failed.\n");

    printf("Solution2 begins: ");
    if(IsBalanced_Solution2(pRoot) == expected)
        printf("Passed.\n");
    else
        printf("Failed.\n");
}

// 完全二叉树
//             1
//         /      \
//        2        3
//       /\       / \
//      4  5     6   7
void Test1()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode7 = CreateBinaryTreeNode(7);

    ConnectTreeNodes(pNode1, pNode2, pNode3);
    ConnectTreeNodes(pNode2, pNode4, pNode5);
    ConnectTreeNodes(pNode3, pNode6, pNode7);

    Test("Test1", pNode1, true);

    DestroyTree(pNode1);
}

// 不是完全二叉树，但是平衡二叉树
//             1
//         /      \
//        2        3
//       /\         \
//      4  5         6
//        /
//       7
void Test2()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);
    BinaryTreeNode* pNode7 = CreateBinaryTreeNode(7);

    ConnectTreeNodes(pNode1, pNode2, pNode3);
    ConnectTreeNodes(pNode2, pNode4, pNode5);
    ConnectTreeNodes(pNode3, NULL, pNode6);
    ConnectTreeNodes(pNode5, pNode7, NULL);

    Test("Test2", pNode1, true);

    DestroyTree(pNode1);
}

// 不是平衡二叉树
//             1
//         /      \
//        2        3
//       /\         
//      4  5        
//        /
//       6
void Test3()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);
    BinaryTreeNode* pNode6 = CreateBinaryTreeNode(6);

    ConnectTreeNodes(pNode1, pNode2, pNode3);
    ConnectTreeNodes(pNode2, pNode4, pNode5);
    ConnectTreeNodes(pNode5, pNode6, NULL);

    Test("Test3", pNode1, false);

    DestroyTree(pNode1);
}


//               1
//              /
//             2
//            /
//           3
//          /
//         4
//        /
//       5
void Test4()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);

    ConnectTreeNodes(pNode1, pNode2, NULL);
    ConnectTreeNodes(pNode2, pNode3, NULL);
    ConnectTreeNodes(pNode3, pNode4, NULL);
    ConnectTreeNodes(pNode4, pNode5, NULL);

    Test("Test4", pNode1, false);

    DestroyTree(pNode1);
}

// 1
//  \
//   2
//    \
//     3
//      \
//       4
//        \
//         5
void Test5()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    BinaryTreeNode* pNode2 = CreateBinaryTreeNode(2);
    BinaryTreeNode* pNode3 = CreateBinaryTreeNode(3);
    BinaryTreeNode* pNode4 = CreateBinaryTreeNode(4);
    BinaryTreeNode* pNode5 = CreateBinaryTreeNode(5);

    ConnectTreeNodes(pNode1, NULL, pNode2);
    ConnectTreeNodes(pNode2, NULL, pNode3);
    ConnectTreeNodes(pNode3, NULL, pNode4);
    ConnectTreeNodes(pNode4, NULL, pNode5);

    Test("Test5", pNode1, false);

    DestroyTree(pNode1);
}

// 树中只有1个结点
void Test6()
{
    BinaryTreeNode* pNode1 = CreateBinaryTreeNode(1);
    Test("Test6", pNode1, true);

    DestroyTree(pNode1);
}

// 树中没有结点
void Test7()
{
    Test("Test7", NULL, true);
}

int _tmain(int argc, _TCHAR* argv[])
{
    Test1();
    Test2();
    Test3();
    Test4();
    Test5();
    Test6();
    Test7();

    return 0;
}