一: 作用
最长公共子序列是一个十分实用的问题,它可以描述两段文字之间的“相似度”,即它们的雷同程度,从而能够用来辨别抄袭。对一段文字进行修改之后,计算改动前后文字的最长公共子序列,将除此子序列外的部分提取出来,这种方法判断修改的部分,往往十分准确。简而言之,百度知道、百度百科都用得上。
二:概念
最长公共子序列,英文缩写为LCS(Longest Common Subsequence)。其定义是,一个序列 S ,如果分别是两个或多个已知序列的子序列,且是所有符合此条件序列中最长的,则 S 称为已知序列的最长公共子序列。而最长公共子串(要求连续)和最长公共子序列是不同的。
举个例子,cnblogs这个字符串中子序列有多少个呢?很显然有27个,比如其中的cb,cgs等等都是其子序列,我们可以看出子序列不见得一定是连续的,连续的那是子串。
我想大家已经了解了子序列的概念,那现在可以延伸到两个字符串了,那么大家能够看出:cnblogs和belong的公共子序列吗?
在你找出的公共子序列中,你能找出最长的公共子序列吗?

从图中我们看到了最长公共子序列为blog,仔细想想我们可以发现其实最长公共子序列的个数不是唯一的,可能会有两个以上,
但是长度一定是唯一的,比如这里的最长公共子序列的长度为4。
三:解决方案
动态规划
现有两个序列X={x1,x2,x3,...xi},Y={y1,y2,y3,....,yi},二维数组C[i,j]: 保存Xi与Yj的LCS的长度。
递推方程为:
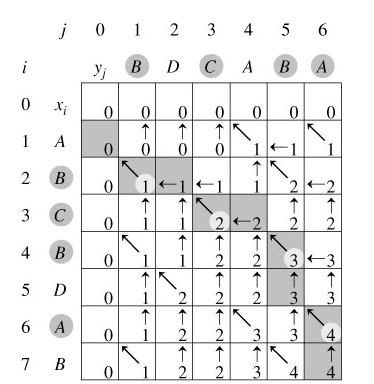
回溯输出最长公共子序列过程:
X=[ A,B,C,B,D,A,B ]
Y=[ B,D,C,A,B,A ]
代码:
#include <iostream>
using namespace std;
#define M 8
#define N 9
//b记录的是,箭头的方向,2代表向左上角,1代表向上,3代表向左,后面根据箭头的方向确定公共序列(此数组也可以省略)
//c记录的是LCS的长度
int b[M+1][N+1] = {0}, c[M+1][N+1] = {0};
int c2[2][M+1] = {0};
/********书上的伪代码*******************************************/
void Lcs_Length(int *x, int *y)
{
int i, j;
//初始化
for(i = 1; i <= M; i++)
c[i][0] = 0;
for(j = 1; j <= N; j++)
c[0][j] = 0;
//根据公式15.14计算,算法复杂度为:O(mn)
for(i = 1; i <= M; i++)
{
for(j = 1; j <= N; j++)
{
//记录计算结果
if(x[i] == y[j])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = 2;
}
else
{
if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = 1;
}
else
{
c[i][j] = c[i][j-1];
b[i][j] = 3;
}
}
}
}
}
//根据 b 确定输出,算法复杂度为:O(m+n)
void Print_Lcs(int *x, int i, int j)
{
if(i == 0 || j == 0)
return;
if(b[i][j] == 2)
{
Print_Lcs(x, i-1, j-1);
cout<<x[i]<<' ';//输出x[i],而不是c中的数
}
else if(b[i][j] == 1)
Print_Lcs(x, i-1, j);
else
Print_Lcs(x, i, j-1);
}
//15.4-2 不使用表b的情况下计算LCS并输出
void Lcs_Length2(int *x, int *y)
{
int i, j;
//初始化
for(i = 1; i <= M; i++)
c[i][0] = 0;
for(j = 1; j <= N; j++)
c[0][j] = 0;
//求LCS的时间没有什么区别,只要把与b有关的去掉就可以了
for(i = 1; i <= M; i++)
{
for(j = 1; j <= N; j++)
{
//第一种情况
if(x[i] == y[j])
c[i][j] = c[i-1][j-1] + 1;
else
{
//第二种情况
if(c[i-1][j] >= c[i][j-1])
c[i][j] = c[i-1][j];
//第三种情况
else
c[i][j] = c[i][j-1];
}
}
}
}
//区别在于输出,根据计算反推出前一个数据,而不是通过查找获得
void Print_Lcs2(int *x, int i, int j)
{
//递归到初始位置了
if(i == 0 || j == 0)
return;
//三种情况,刚好与Lcs_Length2中的三种情况相对应(不是按顺序对应)
//第二种情况
if(c[i][j] == c[i-1][j])
Print_Lcs2(x, i-1, j);
//第三种情况
else if(c[i][j] == c[i][j-1])
Print_Lcs2(x, i, j-1);
//第一种情况
else
{
//匹配位置
Print_Lcs2(x, i-1, j-1);//属于最长子序列的字符肯定不与左和上相等
cout<<x[i]<<' ';
}
}
//15.4-3备忘录版本,类似于递归,只是对做过的计算记录下来,不重复计算
//每一次迭代是x[1..m]和y[1..n]的匹配
int Lcs_Length3(int *x, int *y, int m, int n)
{
//递归结束条件,长度为0,肯定匹配为0
if(m == 0|| n == 0)
return 0;
//若已经计算,直接返回结果
if(c[m][n] != 0)
return c[m][n];
//公式15.14的对应
if(x[m] == y[n])
c[m][n] = Lcs_Length3(x, y, m-1, n-1) + 1;
else
{
int a = Lcs_Length3(x, y, m-1, n);
int b = Lcs_Length3(x, y, m, n-1);
c[m][n] = a > b ? a : b;
}
return c[m][n];
}
//15.4-4(1)使用2*min(m,n)及O(1)的额外空间来计算LCS的长度
void Lcs_Length4(int *x, int *y)
{
int i, j;
//c2是2*min(M,N)的矩阵,初始化
memset(c2, 0 ,sizeof(c2));
//类似于上文的循环,只是i%2代表当前行,(i-1)%2代表上一行,其余内容相似
for(i = 1; i <= N; i++)
{
for(j = 1; j <= M; j++)
{
if(y[i] == x[j])
c2[i%2][j] = c2[(i-1)%2][j-1] + 1;
else
{
if(c2[(i-1)%2][j] >= c2[i%2][j-1])
c2[i%2][j] = c2[(i-1)%2][j];
else
c2[i%2][j] = c2[i%2][j-1];
}
}
}
//输出结果
cout<<c2[N%2][M]<<endl;
}
void Lcs_Length5(int *x, int *y)
{
int i, j, temp = 0;
memset(c2, 0 ,sizeof(c2));
for(i = 1; i <= N; i++)
{
for(j = 1; j <= M; j++)
{
if(y[i] == x[j])
c2[i%2][j] = c2[(i-1)%2][j-1] + 1;
else
{
if(c2[(i-1)%2][j] >= c2[i%2][j-1])
c2[i%2][j] = c2[(i-1)%2][j];
else
c2[i%2][j] = c2[i%2][j-1];
}
}
}
cout<<c2[N%2][M]<<endl;
}
void Print()
{
int i, j;
for(i = 1; i <= M; i++)
{
for(j = 1; j <= N; j++)
cout<<c[i][j]<<' ';
cout<<endl;
}
}
int main()
{
int x[M+1] = {0,1,0,0,1,0,1,0,1};
int y[N+1] = {0,0,1,0,1,1,0,1,1,0};
Lcs_Length(x, y);
// Print();
Print_Lcs(x, M, N);
// Lcs_Length2(x, y);
// Lcs_Length3(x, y, M, N);
// Print();
// Print_Lcs2(x, M, N);
// Lcs_Length4(x, y);
return 0;
}








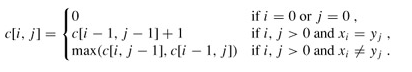














 5775
5775

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








