NFA到DFA的转化

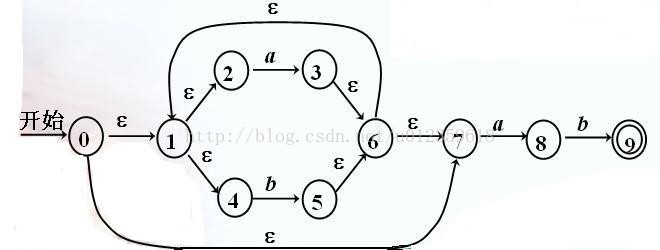
1. 根据上面的状态转换图写出状态转换表，什么！不知道什么是状态转换表？那你来对地方了。状态转换表是转台转换图的另外一种表示形式，如下图，左侧表头0~9表示的

    是状态，上方表头a,b,c表示的是条件。其余部分表示的是后继状态

	a	b	ε
0	∅	∅	1, 7
1	∅	∅	2, 4
2	3	∅	∅
3	∅	∅	6
4	∅	5	∅
5	∅	∅	6
6	∅	∅	1, 7
7	8	∅	∅
8	∅	9	∅
9	∅	∅	∅

2. 求出ε-closure(s)，ε-closure(s)表示由状态s经由条件ε可以到达的 所有状态的集合

ε-closure(0)={0,1,2,4,7}

ε-closure(1)={1,2,4}

ε-closure(2)={2}

ε-closure(3)={1,2,3,4,6,7}

ε-closure(4)={4}

ε-closure(5)={1,2,4,5,6,7}

ε-closure(6)={1,2,4,6,7}

ε-closure(7)={7}

ε-closure(8)={8}

ε-closure(9)={9}

3. 转换，下面就是真正剧情了

首先将初始态的转换闭包ε-closure(0)设为状态A，即A={0,1,2,4,7}，注意这里的状态A是DFA中的，和前面的状态0,1,2,3,4,5没有关系

接着写出状态A经过上面转换图中所有转换条件得到的状态，后继状态里面不包括自身，这里的转换条件包括a和b，注意，不包括ε，转换的一个目的就是消除ε。

ε-closure(0) = A

ε-closure(move(A,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B

ε-closure(move(A,b)) = ε-closure(5) = {1,2,4,5,6,7} = C

ε-closure(move(B,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B

ε-closure(move(B,b)) = ε-closure({5,9}) = {1,2,4,5,6,7,9} = D

ε-closure(move(C,a)) = ε-closure()

ε-closure(move(C,b))

ε-closure(move(D,a)) = ε-closure({3,8}) = {1,2,3,4,6,7,8} = B

ε-closure(move(D,b)) = ε-closure(5) = {1,2,4,5,6,7} = C

4. 画出DFA状态转换表（每一个状态只有一个后继状态）

	a	b
A	B	C
B	B	D
C	B	C
D	B	C

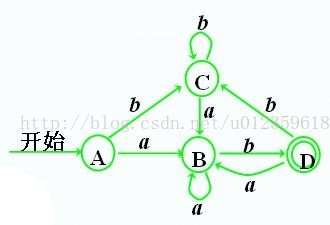
5. 画出DFA状态转换图

6. DFA的最小化

    （1） 消除多余状态

              Ⅰ. 什么是多余状态

                    · 从这个状态出发没有通路到达终态

                    ·  从开始状态出发，任何输入串也不能到达的那个状态

               Ⅱ. 如何消除多余状态

                     删除

                     

             （2）  等价状态

                      Ⅰ. 何为等价状态，对于两个状态s和t

                            ·  一致性条件：状态s和t必须同时为终态或非终态

                            ·  蔓延性条件：对于所有输入符号，状态s和状态t必须转化到等价的状态里

        

                   接下来是关于如何利用上面的两个条件来判断是否为等价状态，来一张复杂的状态转换图，是不是有点晕，哈哈

                  

                   首先，画出状态转换表

                 

                  看1和2，1和2都是非终态，满足条件1，1和2都可以转换成状态2，满足条件2，将两者合并。

                  看6和7，6和7都是终态，满足条件2，6和7都可以转化成状态6，满足条件2，将两者合并。

                  以此类推，当然，2和5也是可以合并的，记住最后的结果只有一种，只要满足合并后的状态最少就行

                 

                   转化

                  1,2→A

                   3,4→B

                   5→C

                   6,7→D

                   列出转化后的转台转换表

                         

                 再画出相应的状态转换图就大功告成啦~~