java实现（2）-AVL树

引言

在上一篇博文中，介绍了二叉查找树。在二叉查找树的基础上，深入研究一下AVL树，并用代码实现核心模块：插入和删除。在本篇博文中主要详细介绍了AVL树的平衡概念，同时介绍解决平衡问题的旋转问题。在实现代码部分详细介绍在插入的时候保证树的平衡。笔者目前整理的一些blog针对面试都是超高频出现的。大家可以点击链接：http://blog.csdn.net/u012403290

技术点

1、AVL树
通俗来说就是一棵的左子树和右子树的高度最多相差1个路径的二叉查找树。所以说AVL树是建立在二叉查找树之上的，我们知道在二叉查找树最坏的情况就是每个节点都只有左(右)儿子，导致二叉查找树变成了一个链表，而AVL树就是为了克服这个问题产生的。比如说下面两颗树：

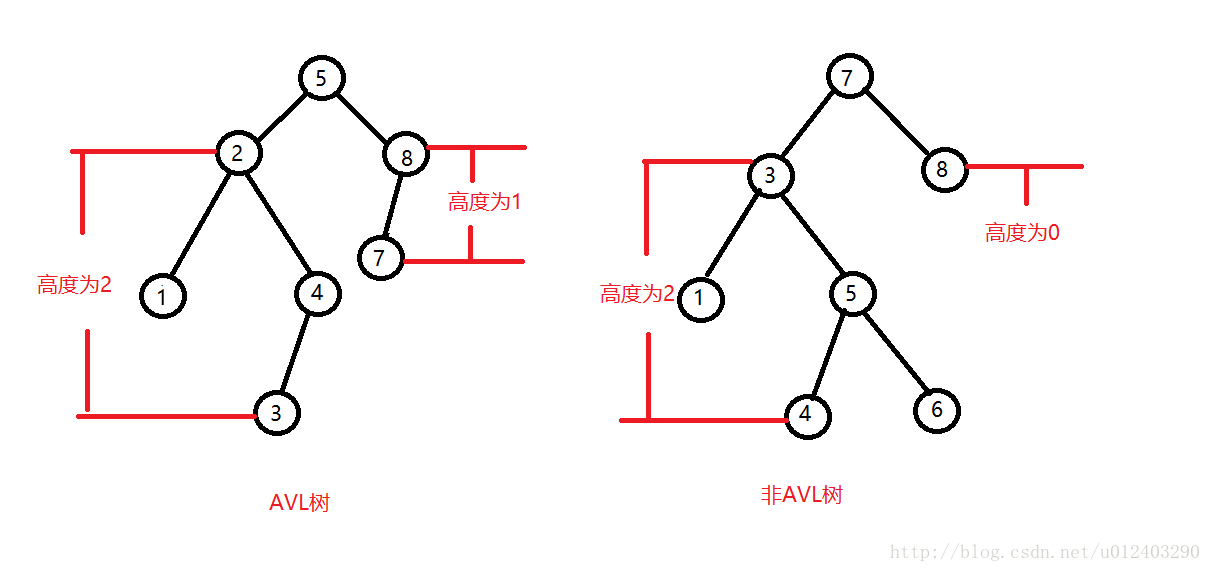
在左图中，对于节点5，它的左子树的高度为2，右子树的高度为1，两者相差1个路径，所以它符合AVL树的定义；在右图中，对于节点7，它的左子树高度为2，右子树高度为0，两者相差2个路径，所以它不符合AVL树的定义。

2、旋转
因为在插入或者删除的时候会导致AVL树变得不平衡，那么就会采用旋转来调整树的新平衡。旋转分为两种，一种是左旋，一种是又旋。节点插入导致的不平衡分为4种情况，假设我们不平衡的节点为N：
①、在N的左儿子的左子树进行一次插入，可以称为LL，这个时候可以通过右旋来解决：

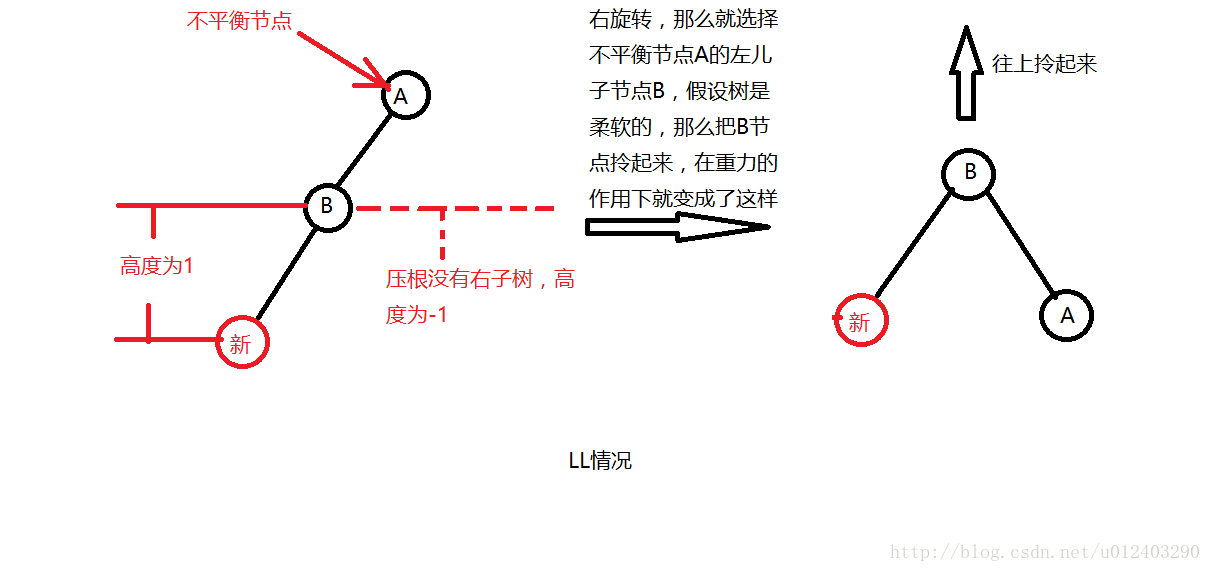
注意，在下面的介绍中，不会再继续标志节点的左右子树的高了。我们用平衡因子BF来标志。我们用|0，1|，绝对值的0和1表示某一个节点的左右子树的高度差，如果值大于1了，就表示这个节点已经不平衡了。

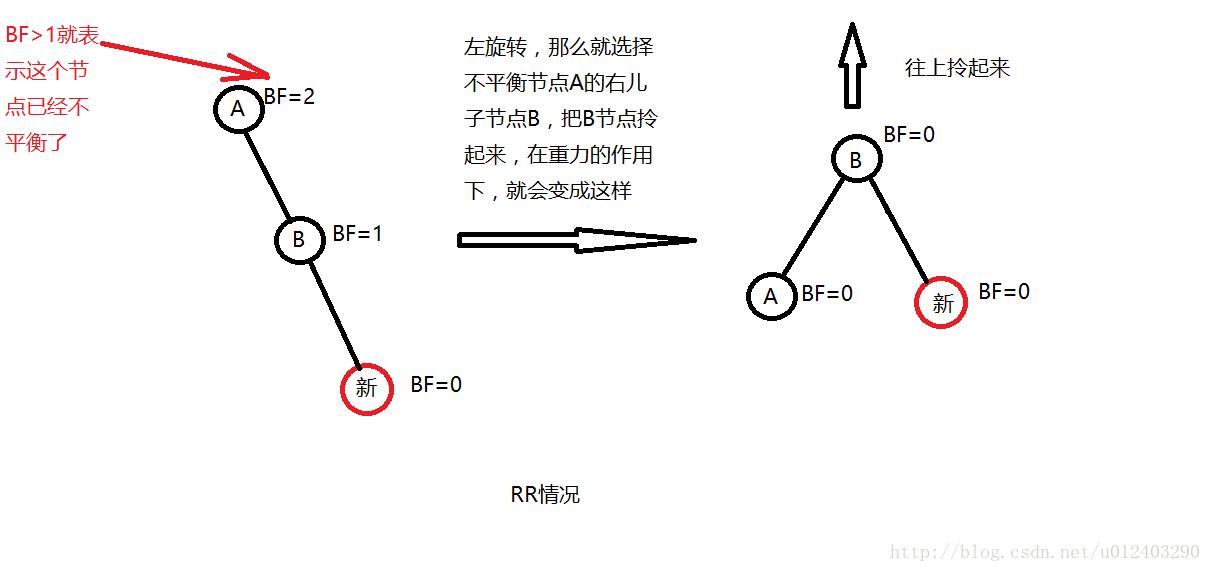
②、在N的右儿子的右子树进行一次插入，可以称为RR，这个时候可以通过左旋来解决：

③、在N的左儿子的右子树进行一次插入，可以称为LR，这个时候就不可以通过一次旋转来解决了，而是要先通过左旋，再通过右旋恢复平衡：

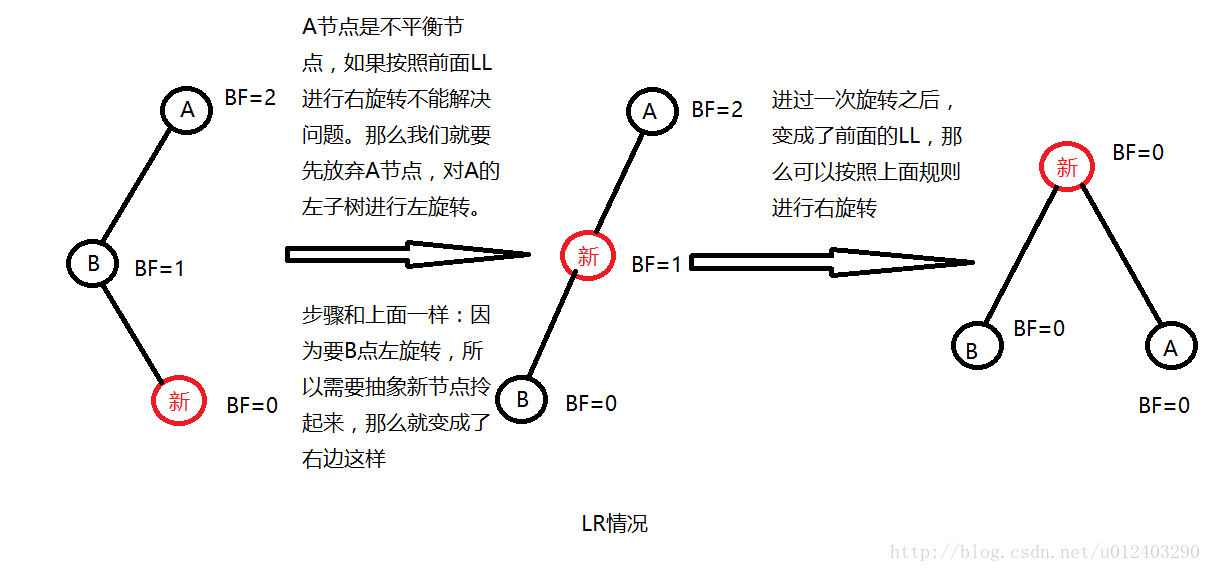
在LR的情况中，如果我们按照之前的那么只能对A节点进行右旋（如果要左旋的话，必须右儿子不为空），按照上面的规则，把B节点直接拎起来会发现这种情况下的树就不是二叉查找树了，因为新节点必然比B节点要大，如果直接把B拎起来，那么新节点就会变成了B的左节点，显然是不行的。所以LR的情况需要进行两次旋转，第一次保证支持二叉查找树，第二次调整平衡。

④、在N的右儿子的左子树进行一次插入，可以称为RL，这个时候和上面一样需要进行两次旋转来解决：

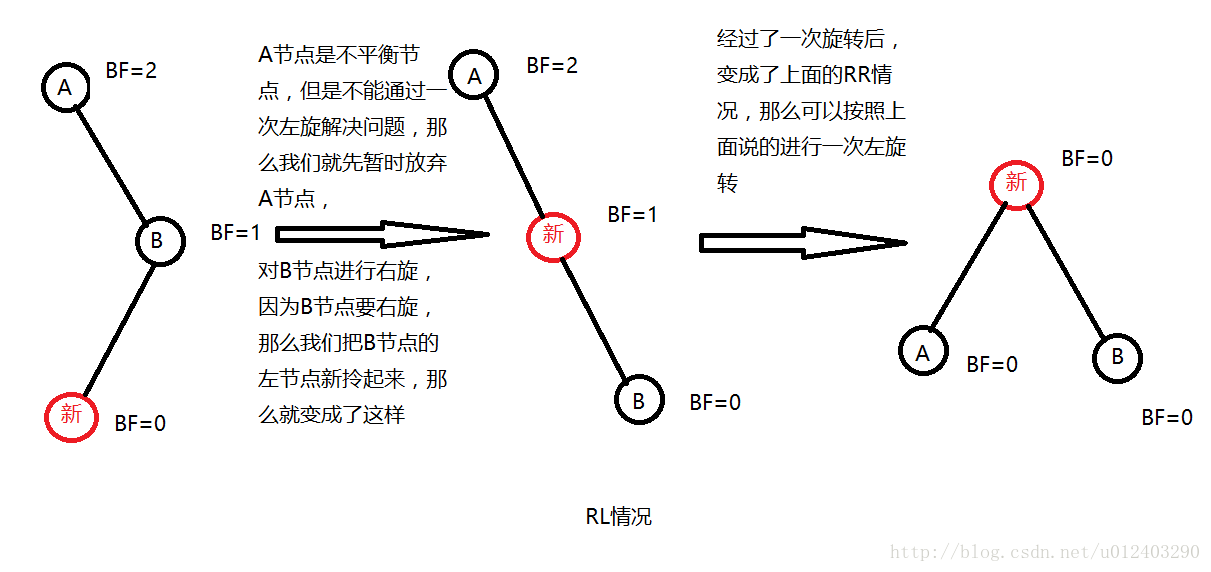
介绍完4种情况，我们做一个总结，方便后面代码实现：在AVL树种插入一个节点N，首先我们肯定是要递归把N插入到它所合适的节点上（什么叫合适的节点，在上一篇博文介绍二叉查找树有说过）。如果插入之后，更新相关节点的高度信息之后，发现没有超过1，那么插入就结束。如果发现某一个节点的BF>1了，表示这个节点所代表的的这颗树已经是不平衡的了，需要按照上面4种情况判断结果，并进行相依的选转操作来保证还是一颗AVL树。

代码实现AVL树的插入

分析完AVL树的性质和它维持平衡的方式，我们对它进行一个简单的实现:
①必须要有一个类来表示一个节点，且这个节点要包含数据部分，左孩子，右孩子和高。
②在插入的过程中必须要更新被影响的节点的高信息。如果发现节点不平衡需要判断是属于哪种情况的不平衡，并采用相应的选择让树恢复平衡。

以下就是实现的代码：

package com.brickworkers;

public class AvlTree<T extends Comparable<? super T>> {

    private static final int MAX_BF = 1;

    //一个枚举类，表示再插入的时候判断是属于什么情况
    private static enum Condition{
        LL, RR, LR, RL;
    }


    //静态内部类表示节点
    private static class AvlNode<T>{
        T data;       //存储的数据
        AvlNode<T> left;//左孩子
        AvlNode<T> right;//右孩子
        int height;//树的高度
        AvlNode(T data, AvlNode<T> lt, AvlNode<T> rt) {
            this.data = data;
            left = lt;
            right = rt;
            height = 0;//新节点插入必然是0高度的
        }
        AvlNode(T data) {
            this(data, null, null);
        }
    }


    //实现插入
    private AvlNode<T> insert(T data, AvlNode<T> node){
        if(node == null){
            return new AvlNode<T>(data);
        }

        if(data.compareTo(node.data) < 0){
            node.left = insert(data, node.left);
        }
        else if(data.compareTo(node.data) > 0){
            node.right = insert(data, node.right);
        }
        else{
            //不能插入一样的数据
        }
        return balance(node);//重新调整树的平衡
    }


    //重新调整树的平衡
    private AvlNode<T> balance(AvlNode<T> node){
        //如果当前节点的左子树比右子树大，且超过了1,那么就有两种情况，就是LL,或者LR
        if(node.left.height - node.right.height > MAX_BF){
            if(node.left.left.height >= node.left.right.height){//LL情况
                singleRotate(node, Condition.LL);
            }else{//否则就是LR情况，就需要进行双旋转
                doubleRotate(node, Condition.LR);

            }
        }
        //如果当前节点的右子树比左子树大，且超过了1，那么就有两种情况，就是RR,或者RL
        else if(node.right.height - node.left.height > MAX_BF){
            if(node.right.right.height >= node.right.left.height){//RR情况
                singleRotate(node, Condition.RR);
            }else{//否则就是RL情况
                doubleRotate(node, Condition.RL);
            }

        }

        //重新修正一下当前节点的高度
        node.height = Math.max(node.left.height, node.right.height) + 1;
        return node;
    }



    //实现单旋转
    private AvlNode<T> singleRotate(AvlNode<T> node, Condition rotateCondition){
        AvlNode<T> pullNode;
        if(rotateCondition == Condition.RR){//如果是左旋操作
            //找准前面我们说的要拎起来的点
            pullNode = node.right;//按我们前面说的就是：左旋，把不平衡节点的右节点拎起来
            node.right = pullNode.left;//先处理不平衡节点，如果pull节点本身就有左节点，要把左边节点交给node作为它的右节点
            pullNode.left = node;//puu节点的左节点变成了node
            //调整节点高度
            node.height = Math.max(node.left.height, node.right.height) + 1;//旋转结束之后，需要重新计算变动节点的高度
            pullNode.height = Math.max(node.height, pullNode.right.height) + 1;
        }else{//右旋操作
            //方式方法和左旋是一样的就不再赘述
            pullNode = node.left;
            node.left = pullNode.right;
            pullNode.right = node;
            node.height = Math.max(node.left.height, node.right.height) + 1;
            pullNode.height = Math.max(pullNode.left.height, node.height) + 1;
        }
        return pullNode;
    }


    //实现双旋转，双旋转其实就是拆分为两个旋转方式。
    private AvlNode<T> doubleRotate(AvlNode<T> node, Condition rotateCondition){
        if(rotateCondition == Condition.RL){//如果是RL，就需要先右旋再左旋
            node.right = singleRotate(node.right, Condition.LL);//先进行一次右旋
            return singleRotate(node, Condition.RR);//再进行一次左旋
        }else{
            node.left = singleRotate(node.left, Condition.RR);//先进行一次左旋
            return singleRotate(node, Condition.LL);//在进行一次右旋
        }
    }


}

这里实现了核心的旋转和插入，用一个内部枚举类控制当插入之后，重新平衡的时候用于标记当前属于什么情况，该调用什么方法。AVL节点内部类用于表示树中的每一个节点，这个节点包含了AVL特有的高度信息。当然了，在删除的过程也会导致树变成不平衡的，大家有兴趣可以建立在上一篇博文二叉查找树的博文之上然后参考上面的实现，对删除方法进行修改。不过在源代码中，我遗漏了一点，如果某一个计算一个空节点的高，那么应该返回-1，在最上面的图中我已经解释了为什么。大家自己加入到上面的代码中，进行补充。

如果博文存在什么问题，或者想法请留言，希望对大家有所帮助。