Java内排序算法二

6.归并排序

• 思想：运用分治法思想先使每个子序列有序，再将两个已经排序的序列合并成一个序列的操作。若将两个有序表合并成一个有序表，称为二路归并。
• 时间复杂度：平均、最佳、最差时间复杂度均为O(nlgn)
• 代码如下：一般用递归求解：

package xianggen.sortsummary;
/**
 * 
 * MergeSort.java
 * @author xianggen
 * @date 2016年7月25日 下午3:31:00
 */
public class MergeSort {
    public static void main(String[] args) {
        int[] arr={3,5,7,1,4,2,8,9,0,6};
        recursiveMergeSort(arr,0,arr.length-1);

        for(int i=0;i<arr.length;i++)
            System.out.print(arr[i]+" ");
        System.out.println();
    }

     public static int[] recursiveMergeSort(int[] arr, int low, int high) {  
            int mid = (low + high) / 2;  
            if (low < high) {  
                // 左边  
                recursiveMergeSort(arr, low, mid);  
                // 右边  
                recursiveMergeSort(arr, mid + 1, high);  
                // 左右归并  
                merge(arr, low, mid, high);  
            }  
            return arr;  
        }  

        public static void merge(int[] arr, int low, int mid, int high) {  
            int[] temp = new int[high - low + 1];  
            int i = low;// 左指针  
            int j = mid + 1;// 右指针  
            int k = 0;  

            // 把较小的数先移到新数组中  
            while (i <= mid && j <= high) {  
                if (arr[i] < arr[j]) {  
                    temp[k++] = arr[i++];  
                } else {  
                    temp[k++] = arr[j++];  
                }  
            }  

            // 把左边剩余的数移入数组  
            while (i <= mid) {  
                temp[k++] = arr[i++];  
            }  

            // 把右边边剩余的数移入数组  
            while (j <= high) {  
                temp[k++] = arr[j++];  
            }  

            // 把新数组中的数覆盖arr数组  
            for (int k2 = 0; k2 < temp.length; k2++) {  
                arr[k2 + low] = temp[k2];  
            }  
        }  
}

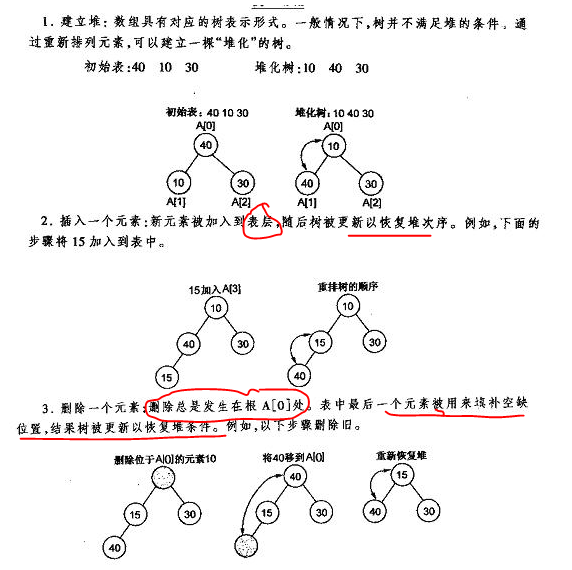
7.堆排序

二叉堆：二叉堆是完全二叉树或者是近似完全二叉树。

父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

每个结点的左子树和右子树都是一个二叉堆。

其它几种堆（二项式堆，斐波纳契堆等）用的较少，一般将二叉堆就简称为堆。堆排序是原址排序，同快排，空间开销小！

• 思想：初始时把要排序的n个数的序列看作是一棵顺序存储的完全二叉树（一维数组存储二叉树），调整它们的存储序，使之成为一个堆，将堆顶元素输出，得到n 个元素中最小(或最大)的元素，这时堆的根节点的数最小（或者最大）。然后对前面(n-1)个元素重新调整使之成为堆，输出堆顶元素，得到n 个元素中次小(或次大)的元素。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。称这个过程为堆排序。
• 时间复杂度：平均、最佳、最差时间复杂度均为O(nlogn )
• **代码如下：实现堆排序需解决两个问题：1. 如何将n 个待排序的数建成堆；2. 输出堆顶元素后，怎样调整剩余n-1 个元素，使其成为一个新堆。

先上图解：

package xianggen.sortsummary;
/**
 * 堆排序！
 * 两个过程：建堆，堆顶与堆的最后一个元素交换位置
 * HeapSort.java
 * @author xianggen
 * @date 2016年8月16日 上午10:18:14
 */
public class HeapSort {
    public static void main(String[] args) {
        int[] arr={3,5,7,1,4,2,8,9,0,6};
        heapSort(arr,arr.length);
        printHeap(arr);

    }
    public static void heapSort(int[] arr,int length){
        buildHeap(arr,length);
        for(int i=arr.length-1;i>0;i--){
            swap(arr,0,i);
            heapAdjust(arr,0,i);
        }
    }

    /**
     * 堆初始数组建最大堆！ 
     * arr[0..length-1]建成堆 ，其中arr[0]为最大值，将其与arr[length-1]交换
     * @param arr,length
     */
    public static void buildHeap(int[] arr,int length){
        //!!! 从最后一个有孩子的节点的位置开始堆调整： i= (length -1) / 2  
        for(int i=(length-1)/2;i>=0;i--){
              heapAdjust(arr,i,length);         
        }
    }

    /**
     * 这是堆排序的关键操作！！功能将一个节点拖拽至子树的合适位置！
     * @param arr
     * @param index
     * @param length
     */
    public static void heapAdjust(int[]arr, int index,int length){
        int tmp=arr[index],child=2*index+1;  //左孩子结点的位置
        while(child<length){
            if(child+1<length&&arr[child]<arr[child+1]){
                child++;    //如果位于index的节点有右孩子且其值比左孩子大，则得到右孩子的索引值
            }
            if(arr[index]<arr[child]){   // 若父节点小于孩子(较大的)，则把父节点拖拽下来
                arr[index]=arr[child];
                index=child;
                child=2*index+1;    //注意这个更新，千万不要忘记。(保持刚开始时child指向的是左孩子)
            }else{
                break;   //！！！ 如果当前待调整结点大于它的左右孩子，则不需要调整，直接退出 
            }
            arr[index]=tmp;   // 当前待调整的结点放到比其大的孩子结点位置上  
        }
    }

    public static void swap(int[] arr,int i,int j){
        int tmp=arr[i];
        arr[i]=arr[j];
        arr[j]=tmp;
    }

    public static void printHeap(int[] arr){
        for(int i=0;i<arr.length;i++)
            System.out.print(arr[i]+" ");
        System.out.println();
    }

}

8.计数排序

http://www.cnblogs.com/eaglet/archive/2010/09/16/1828016.html

计数排序是一个类似于桶排序的排序算法，其优势是对已知数量范围的数组进行排序。它创建一个长度为这个数据范围的数组C，C中每个元素记录要排序数组中对应记录的出现个数。这个算法于1954年由 Harold H. Seward 提出。

依靠一个辅助数组来实现，不基于比较，算法复杂度为 O(n) ，但由于要一个辅助数组C，所以空间复杂度要大一些，由于计算机的内存有限，这种算法不适合范围很大的数的排序。

最坏情况运行时间：O(n+k)；最好情况运行时间：O(n+k)，k为待排数组中的最大值。

看一个例子：

/**
 * 
 * CountingSort.java
 * @author xianggen
 * @date 2016年8月16日 下午2:51:08
 */
public class CountingSort {
    public static void main(String[] args) {
        int[] arr={3,3,7,1,4,2,8,19,0,6};
        int[] res=countSort(arr);
        printHeap(res);

    }

    public static int[] countSort(int[] arr){
        int max=arr[0];
        for(int i=1;i<arr.length;i++)
            if(arr[i]>max)
                max=arr[i];
        int[] tmpArr=new int[max+1];
        int[] res=new int[arr.length];

        for(int i=0;i<arr.length;i++)
            tmpArr[arr[i]]++;   //此时res[i]表示等于i的元素个数  

        for(int i=1;i<=max;i++)
            tmpArr[i]+=tmpArr[i-1]; //此时res[i]表示小于或者等于i的元素个数 
        // 把输入数组中的元素放在输出数组中对应的位置
        for(int i=arr.length-1;i>=0;i--){
            res[tmpArr[arr[i]]-1]=arr[i]; // 用tmpArr数组来确定arr[i]的下标！
            tmpArr[arr[i]]--; // 该操作使得下一个值为arr[i]的元素直接进入输出数组中arr[i]的前一个位置  
        }
        return res;
    }

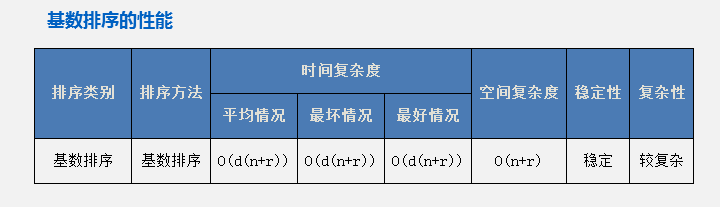
8.基数排序

http://www.cnblogs.com/Braveliu/archive/2013/01/21/2870201.html

根据从低位还是从高位开始排序，基数排序分为两种：LSD（Least significant digital）或MSD（Most significant digital）

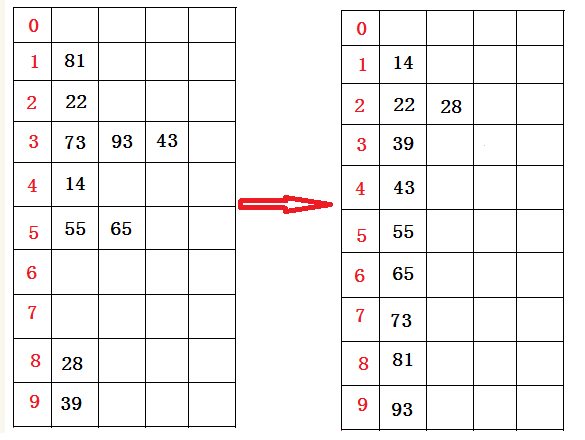
待排数组：73 22 93 43 55 14 28 65 39 81
使用LSD排序：先根据个位数的数值，在遍历数据时将它们各自分配到编号0至9的桶（个位数值与桶号一一对应）中；接着根据十位数值再进行一次分配。

每位基于计数排序：

package xianggen.sortsummary;
/**
 * 基数排序，假定每位的排序是计数排序
 * RadixSort.java
 * @author xianggen
 * @date 2016年8月16日 下午5:34:48
 */
public class RadixSort {
    public static void main(String[] args) {
        int[] arr={3,3,7,1,4,2,8,11,0,6};
        radixSort(arr);
    }

    public static void radixSort(int[] arr){
        int d=getOffset(arr);
        int radix=10;
        int[] count=new int[radix];
        int[] bucket=new int[arr.length];

        // 按照从低位到高位的顺序执行排序过程
        for(int i=0;i<d;i++){

            // 置空各个桶的数据统计,这个操作一定不能忘记！
            for (int j=0; j<radix; j++) {
                count[j] = 0;
            }
            // 统计各个桶将要装入的数据个数
            for(int j=0;j<arr.length;j++){
                count[getDigit(arr[j],i)]++;
            }

            for(int j=1;j<radix;j++)
                count[j]=count[j]+count[j-1];
            // 将数据依次装入桶中,从右向左扫描，保证排序稳定性
            for(int j=arr.length-1;j>=0;j--){
                int index=getDigit(arr[j],i);
                bucket[count[index]-1]=arr[j];
                count[index]--;
            }
            // 将已分配好的桶中数据再倒出来，此时已是对应当前位数有序的表
            for(int j=0;j<bucket.length;j++)
                arr[j]=bucket[j];
        }
        for(int j=0;j<bucket.length;j++)
            System.out.print(arr[j]+" ");
        System.out.println();
    }

    /**
     * 获取数组中元素中最大的位数！
     * @param arr
     * @return
     */
    public static int getOffset(int[] arr){
        int result=1;
        for(int i=0;i<arr.length;i++){
            int tmp=1,k=10;
            while(arr[i]>=k){
                k*=10;
                tmp++;
            }
            if(tmp>result)
                result=tmp;
        }
        return result;
    }
    /**
     * // 获取number这个数的(d+1)位数上的数字,从右往左开始(个位计起)
     * @param number
     * @param d
     * @return
     */
    public static int getDigit(int number,int d){
        int a[]={1,10,100};
        return ((number/a[d])%10);
    }

}