POJ 1087 A Plug for UNIX【最大流】

题意：n个不同类型插口的插座，m个电器和电器对应的插口类型，c种插口转换器（每种无限多且可嵌套），求最少多少个电器不能找到插座。

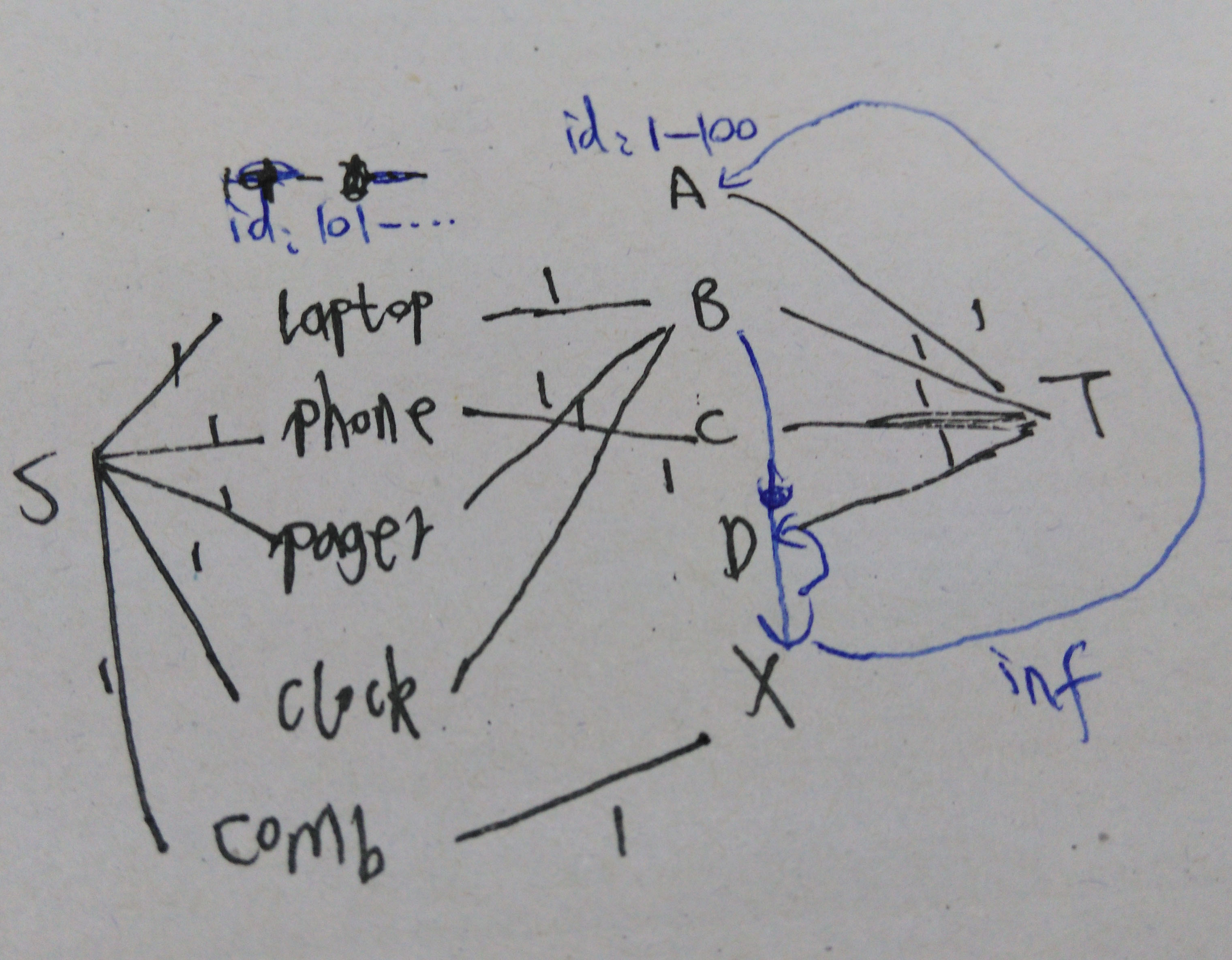
用电器总数m-最大流，建图：

插座ID从1开始，电器ID从101开始，浪费空间来让代码好写点。

#include <cstdio>
#include <cmath>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
#define eps 10^(-6)
#define Q_CIN ios::sync_with_stdio(false);
#define REP( i , n ) for ( int i = 0 ; i < n ; ++ i )
#define FOR( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define CLR( a , x ) memset ( a , x , sizeof (a) );
#define RE freopen("1.in","r",stdin);
#define WE freopen("1.out","w",stdout);
#define MOD 10009
#define debug(x) cout<<#x<<":"<<(x)<<endl;
#define sc(x) scanf("%d",&x);
#define lson i<<1,l,m
#define rson i<<1|1,m+1,r
const int maxn=400;
const int maxm=1e6+5;
const int inf = 0x3f3f3f3f;
int cap[maxn][maxn],dis[maxn];
int ss,tt;
map<string,int>p;

int bfs(int s,int t){
    queue<int>q;
    q.push(s);
    CLR(dis,-1);
    dis[s]=0;
    while(!q.empty()){
        int cur=q.front();q.pop();
        FOR(i,s,t){
            if(cap[cur][i]&&dis[i]<0){
                dis[i]=dis[cur]+1;
                q.push(i);
            }
        }
    }
    return dis[t]>0;
}
int dfs(int s,int t,int low){
    int flow;
    if(s==tt)   return low;
    FOR(i,ss,tt){
        if(cap[s][i]
        && (dis[i]==dis[s]+1)
        && (flow=dfs(i,t,min(low,cap[s][i]))) ){
            cap[s][i]-=flow;
            cap[i][s]+=flow;
            return flow;
        }
    }
    return 0;
}

int maxFlow(){
    int tans=0;
    while(bfs(ss,tt))
        tans+=dfs(ss,tt,inf);
    return tans;
}

int main(){
//    RE
    char ch,ch1;
    int t1,cnt=0;
    string s1,s2;
    ss=0,tt=300;
    int num1=0,num2=100;//浪费点空间,从1开始
    CLR(cap,0);
    cin>>t1;
    while(t1--){
        cin>>s1;
        p[s1]=++num1;  
        cap[num1][tt]=1;        //插座向汇点建边
    }
    cin>>t1;
    while(t1--){
        cin>>s1>>s2;
        p[s1]=++num2;
        cnt++;
        if(!p[s2])
            p[s2]=++num1;
        cap[num2][p[s2]]=1;     //电器向插座建边
        cap[ss][num2]=1;        //源点向电器建边
    }
    cin>>t1;
    while(t1--){
        cin>>s1>>s2;
        cap[p[s1]][p[s2]]=inf;   //A转B，A向B建INF边
    }
    cout<<cnt-maxFlow()<<endl;
    return 0;
}

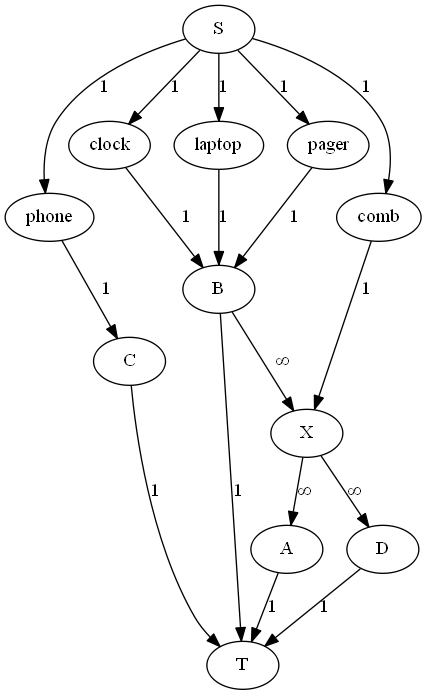
digraph G{
	S->laptop[label="1"];
	S->phone[label="1"];
	S->pager[label="1"];
	S->clock[label="1"];
	S->comb[label="1"];
	laptop->B[label="1"];
	phone->C[label="1"];
	pager->B[label="1"];
	clock->B[label="1"];
	comb->X[label="1"];
	A->T[label="1"];
	B->T[label="1"];
	C->T[label="1"];
	D->T[label="1"];
	B->X[label="∞"];
	X->A[label="∞"];
	X->D[label="∞"];
}