计数排序

• 排序算法的下界
• 计数排序

排序算法的下界

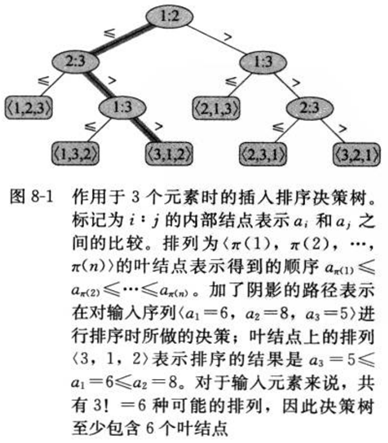
在一般的排序算法中，都是通过比较，确定元素之间的关系而确定顺序，
只要是比较就只有三种情况， “<”、“=”、“>”
我们将“<”、“=”放在一起，则只剩下两种情况 “<=”、“>”
这样想我们就可以就排序过程看成是决策树

这是一颗完全二叉树。

树的高 $h >= \lg (n!) = O(n \lg n)$

在最坏情况下,任何比较排序都需要做$\Omega( {n \lg n})$ 次比较

计数排序

其实我们不用具体的知道一个数与其他数的关系，

对每一个输入元素，确定比其小的元素的个数

就能确定他的位置了。

public static void sort(int[] data){
        int len = data.length, max = data[0];
        int output[] = new int[len];
        for(int i = 1; i < len; i ++ ){
            if(data[i] > max){
                max = data[i];
            }
        }
        int c[] = new int[max + 1];
        for(int i = 0; i < len; i ++){
            c[data[i]] ++;
        }
        for(int i = 2; i <= max; i ++){
            c[i] = c[i] + c[i-1];
        }
        for(int i = len - 1 ; i >= 0 ; i --){
            output[c[data[i]]-1] = data[i];
            c[data[i]] --;
        }
        for(int i = 0; i < len; i ++){
            data[i] = output[i];
        }

    }

此方法中并没有比较，不管这个元素在此数组中是什么位置，她在整个数域中的位置是一定的，C数组就是这么一个数域，值确定了其在C中的索引，接下来的任务就是从前向后数数。一次扫描就够了。所以计数排序的时间复杂为线性即 $O(n)$

---

参考文献

[1] 算法之道
[2] 算法导论